1 câu hỏi trắc nghiệm thuộc Dạng 2: Quan hệ giữa các góc trong hình học:

Trắc nghiệm Chuyên đề toán 9 Chuyên đề 10: Rèn luyện kĩ năng tìm lời giải bài toán hình học có đáp án

Dạng 2: Quan hệ giữa các góc trong hình học:

1535 lượt thi
1 câu hỏi
45 phút

Danh sách câu hỏi

Câu 1:

△

ABC nội tiếp trong đường tròn tâm O, với AB > AC. Kẻ đường cao AH, bán kính OA. Chứng minh

\hat{O A H} = \hat{A C B} - \hat{A B C}

Xem đáp án

Cách giải 1: (Hình 1)

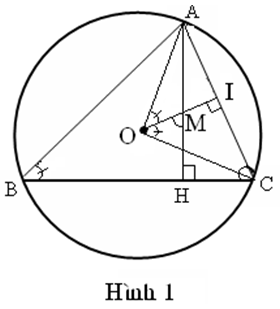
Cho tam giác ABC nội tiếp trong đường tròn tâm O, với AB > AC. Kẻ đường cao AH, bán kính OA. (ảnh 1)

Kẻ OI $⊥$ AC cắt AH ở M
Ta có: $\hat{O M H} = \hat{A C B}$ (góc có các cặp cạnh tương ứng vuông góc)
$\hat{A O M} = \hat{A B C}$ (cùng bằng $\frac{1}{2}$ sđ $\hat{A C}$ )
Trong $△$ OAM thì: $\hat{O M H} = \hat{A O M} + \hat{O A H}$ (Góc ngoài tam giác)
Hay $\hat{A C B} = \hat{A B C} + \hat{O A H}$
Vậy: $\hat{O A H} = \hat{A C B} - \hat{A B C}$ (Đpcm)

Cách giải 2: (Hình 2)

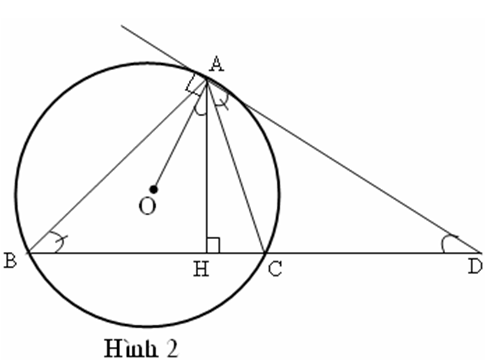
Cho tam giác ABC nội tiếp trong đường tròn tâm O, với AB > AC. Kẻ đường cao AH, bán kính OA. (ảnh 2)

Kẻ tiếp tuyến với đường tròn tại A cắt BC ở D .
Ta có: $\hat{A B C} = \hat{C A D}$ (1) (Cùng chắn )
$\hat{O A H} = \hat{A D C}$ (2) (góc có các cặp cạnh tương ứng vuông góc)
Cộng từng vế của (1) và (2) Ta được: $\hat{A B C} + \hat{O A H} = \hat{C A D} + \hat{A D C}$
Mà $\hat{C A D} + \hat{A D C} = \hat{A C B}$ (góc ngoài tam giác)

$\Rightarrow \hat{A B C} + \hat{O A H} = \hat{A C B}$

Vậy: $\hat{O A H} = \hat{A C B} - \hat{A B C}$ (Đpcm)

Cách giải 3: (Hình 3)

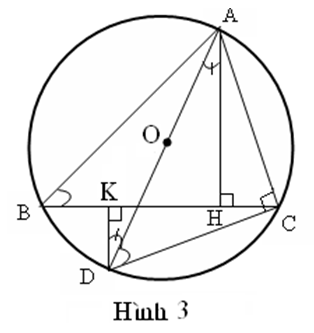
Cho tam giác ABC nội tiếp trong đường tròn tâm O, với AB > AC. Kẻ đường cao AH, bán kính OA. (ảnh 3)

Kẻ đường kính AOD
Kẻ DK $⊥$ BC
Ta có DK // AH $\Rightarrow \hat{O A H} = \hat{O D K}$ (1) (so le trong)
$\hat{A B C} = \hat{A D C}$ (2) (góc nội tiếp cùng chắn $\hat{A C}$ )
Cộng từng vế của (1) và (2) Ta được $\hat{O A H} + \hat{A B C} = \hat{O D K} + \hat{A D C} = \hat{K D C}$
Mà: $\hat{K D C} = \hat{A C B}$ (góc có các cặp cạnh tương ứng vuông góc)
$\Rightarrow \hat{O A H} + \hat{A B C} = \hat{A C B}$ . Vậy $\hat{O A H} = \hat{A C B} - \hat{A B C}$ (Đpcm)

Cách giải 4: (Hình 4)

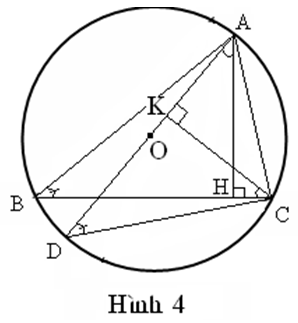
Cho tam giác ABC nội tiếp trong đường tròn tâm O, với AB > AC. Kẻ đường cao AH, bán kính OA. (ảnh 4)

Kẻ đường kính AOD
Kẻ CK $⊥$ AD
Ta có: $\hat{O A H} = \hat{K C B}$ (1) (góc có các cặp cạnh tương ứng vuông góc)

$\hat{A B C} = \hat{A D C}$ (2) (góc nội tiếp cùng chắn $\hat{A C}$ )
Cộng từng vế của (1) và (2) Ta được: $\hat{O A H} + \hat{A B C} = \hat{K C B} + \hat{A D C}$
Mà: $\hat{A D C} = \hat{K C A}$ (góc có các cặp cạnh tương ứng vuông góc)

$\Rightarrow \hat{O A H} + \hat{A B C} = \hat{K C B} + \hat{K C A} = \hat{A C B}$
Vậy: $\hat{O A H} = \hat{A C B} - \hat{A B C}$ (Đpcm)

Cách giải 5: (Hình 5)

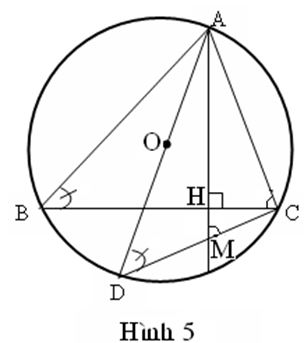
Cho tam giác ABC nội tiếp trong đường tròn tâm O, với AB > AC. Kẻ đường cao AH, bán kính OA. (ảnh 5)

Kẻ đường kính AOD
Gọi M là giao điểm của AH và DC
Ta có: $\hat{A M C} = \hat{A C B}$ (1) (góc có cạnh các cặp cạnh tương ứng vuông góc)
$\hat{A D M} = \hat{A B C}$ (2) (góc nội tiếp cùng chắn $\hat{A C}$ )
Trừ từng vế của (1) và (2) Ta được: $\hat{A M C} - \hat{A D M} = \hat{A C B} - \hat{A B C}$
Mà: $\hat{O A H} = \hat{A C B} - \hat{A B C}$ (góc ngoài tam giác)
Vậy $\hat{O A H} = \hat{A C B} - \hat{A B C}$ (Đpcm)

Cách giải 6: (Hình 6)

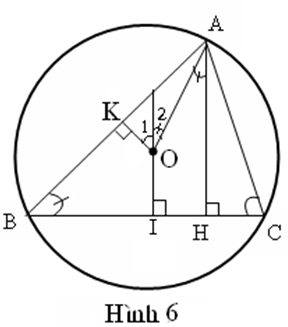
Cho tam giác ABC nội tiếp trong đường tròn tâm O, với AB > AC. Kẻ đường cao AH, bán kính OA. (ảnh 6)

Kẻ OI $⊥$ BC và OK $⊥$ AB
Ta có: $\hat{O A H} = \hat{O_{2}}$ (1) (so le trong)

$\hat{A B C} = \hat{O_{1}}$ (2) (góc có các cặp cạnh tương ứng vuông góc)
Cộng từng vế của (1) và (2) Ta được $\hat{O A H} + \hat{A B C} = \hat{O_{1}} + \hat{O_{2}}$
Mà $\hat{O_{1}} + \hat{O_{2}} = \hat{A C B}$ (Cùng bằng $\frac{1}{2}$ sđ $\hat{A B}$ )

$\Rightarrow \hat{O A H} + \hat{A B C} = \hat{A C B}$

Vậy $\hat{O A H} = \hat{A C B} - \hat{A B C}$ (Đpcm)

Cách giải 7: (Hình 7)

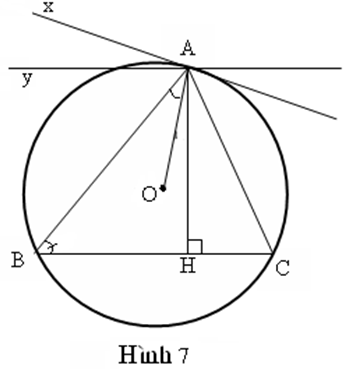
Cho tam giác ABC nội tiếp trong đường tròn tâm O, với AB > AC. Kẻ đường cao AH, bán kính OA. (ảnh 7)

Tại A kẻ tiếp tuyến Ax và đường thẳng Ay // BC
Ta có: $\hat{O A H} = \hat{x A y}$ (1) (góc có các cặp cạnh tương ứng vuông góc)
$\hat{A B C} = \hat{B A y}$ (2) (so le trong)
Cộng từng vế của (1) và (2) Ta được: $\hat{O A H} + \hat{A B C} = \hat{x A y} + \hat{B A y} = \hat{x A B}$
Mà: $\hat{x A B} = \hat{A C B}$ (góc nội tiếp cùng chắn $\hat{AB}$ )

$\Rightarrow \hat{O A H} + \hat{A B C} = \hat{A C B}$
Vậy $\hat{O A H} = \hat{A C B} - \hat{A B C}$ (Đpcm)

Bắt đầu thi ngay