1 câu hỏi trắc nghiệm thuộc Dạng 5 : Chứng minh các điểm cùng thuộc một đường tròn có đáp án

Trắc nghiệm Chuyên đề toán 9 Chuyên đề 10: Rèn luyện kĩ năng tìm lời giải bài toán hình học có đáp án

Dạng 5 : Chứng minh các điểm cùng thuộc một đường tròn có đáp án

1534 lượt thi
1 câu hỏi
45 phút

Danh sách câu hỏi

Câu 1:

Cho tam giác đường phân giác BN và tâm O của đường tròn nội tiếp trong tam giác. Từ A kẻ một tia vuông góc với tia BN, cắt BC tại H. Chứng minh bốn điểm A; O; H; C nằm trên một đường tròn.

Xem đáp án

Trường hợp 1: H và O nằm cùng phía với AC

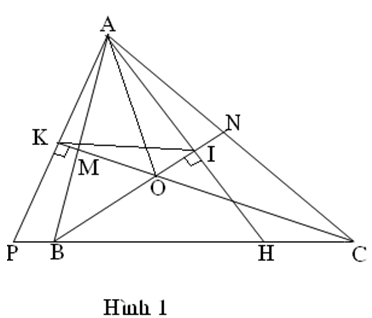
Cho tam giác đường phân giác BN và tâm O của đường tròn nội tiếp trong tam giác. (ảnh 1)

Trường hợp 2: H và O nằm khác phía với AC

Cho tam giác đường phân giác BN và tâm O của đường tròn nội tiếp trong tam giác. (ảnh 2)

Gợi ý: Gọi I là giao điểm của AH và BN. Kẻ AP vuông góc với CO cắt AB tại P. M là giao điểm của OC và AB, K là giao điểm của OC và AP.

Cách giải 1:
Xét $△$ ACP có CK vừa là phân giác vừa là đường cao nên CK cũng là đường trung tuyến, đường trung trực => KA = KP (1)
Xét ABH có BI vừa là phân giác vừa là đường cao nên BI cũng là đường trung tuyến, đường trung trực => IA = IH (2)
Từ (1) và (2) ta có: IK là đường trung bình trong tam giác APH
$\Rightarrow \hat{I K O} = \hat{O C H}$ ( Hình 1)
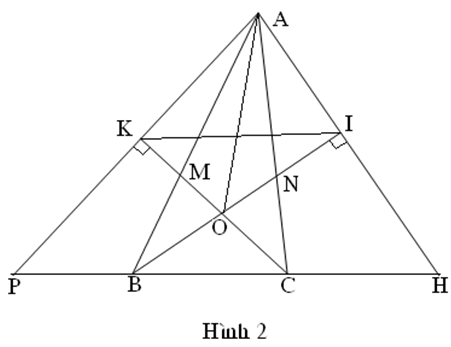
Hoặc $\hat{I K O} + \hat{O C H} = 180^{\circ}$ (Hình 2)
Xét tứ giác AKOI có $\hat{I} = \hat{K} = 90^{\circ}$ => AKOI là tứ giác nội tiếp Tứ giác AOHC nội tiếp được => A; O; H; C cùng nằm trên một đường tròn.

Cách giải 2:
Ta có BN là đường trung trực của AH $\Rightarrow \hat{B H O} = \hat{B A O}$ mà $\hat{B A O} = \hat{O A C}$ nên $\hat{B H O} = \hat{O A C}$ => Tứ giác AOHC nội tiếp được. => A; O; H; C cùng nằm trên một đường tròn.

Cách giải 3:
$△$ ABI là tam giác vuông nên $\hat{I B A} + \hat{B A I} = 180^{\circ}$ hay $\hat{I B A} + \hat{B A O} + \hat{O A I} = 180^{\circ}$ Suy ra: $\hat{O A I} + \frac{\hat{B}}{2} + \frac{\hat{A}}{2} = 90^{\circ}$ => $\hat{O A I}$ bằng (hoặc bù) với góc $\hat{O C H} \Rightarrow$ Tứ giác AOHC nội tiếp được => A; O; H; C cùng nằm trên một đường tròn.

Cách giải 4:
* Đối với (Hình 1) ta có $\hat{A H C} = 90^{\circ} + \frac{\hat{B}}{2}$ Góc ngoài trong tam giác
$\hat{A O C} = 90^{\circ} + \frac{\hat{B}}{2}$ (Vì O là tâm của đường tròn nội tiếp)
$\Rightarrow \hat{A H C} = \hat{A O C} \Rightarrow$ Tứ giác AOHC nội tiếp được => A; O; H; C cùng nằm trên một đường tròn.
* Đối với (Hình 2) Xét trong tam giác IBH ta có $\hat{A H C} = 90^{\circ} - \frac{\hat{B}}{2}$
$\hat{A O C} = 90^{\circ} + \frac{\hat{B}}{2}$ (Vì O là tâm của đường tròn nội tiếp) $\Rightarrow \hat{A H C} + \hat{A O C} = 180^{\circ}$
Tứ giác AOHC nội tiếp được => A; O; H; C cùng nằm trên một đường tròn.

Cách giải 5:
Ta có $\hat{A O N} = \frac{\hat{A} + \hat{B}}{2}$ (Góc ngoài ở đỉnh O của tam giác AOB)
$\Rightarrow \hat{A O H} = \hat{A} + \hat{B} \Rightarrow \hat{A O H} + \hat{A C H} = 180^{\circ}$ (Hình 1)
hoặc $\hat{O A H} = \hat{A C H} = \hat{A} + \hat{B}$ (Hình 2)
=> Tứ giác AOHC nội tiếp được => A; O; H; C cùng nằm trên một đường tròn

Bắt đầu thi ngay