12 câu hỏi trắc nghiệm thuộc Dạng 2: Giải bài toán bằng cách lập phương trình, hệ phương trình có đáp án

Câu 1:

Hai ô tô khởi hành cùng một lúc từ thành phố A đến thành phố B cách nhau 450 km với vận tốc không đổi. Vận tốc xe thứ nhất lớn hơn vận tốc xe thứ hai 10km/h nên xe thứ nhất đến trước xe thứ hai 1,5 giờ. Tính vận tốc mỗi xe

Xem đáp án

Gọi vận tốc xe thứ nhất là x (km/h) (điều kiện: x > 10)

Thì vận tốc xe thứ hai là x – 10(km/h)

Thời gian xe thứ nhất đi hết quãng đường AB là: $\frac{1}{x}$ (h)

Thời gian xe thứ hai đi hết quãng đường AB là: $\frac{1}{x - 10}$ (h)

Vì nên xe thứ nhất đến trước xe thứ hai 1,5 giờ ta có phương trình:

$\frac{450}{x - 10} - \frac{450}{x} = \frac{3}{2}$ $\Rightarrow 900 x - 900 x + 9000 = 3 x^{2} - 30 x$ ; $\sqrt{Δ} = 110$

$x_{1} = \frac{10 + 110}{2} = 60$ (nhận), $x_{2} = \frac{10 - 110}{2} = - 50$ (loại)

Vậy vận tốc xe thứ nhất là 60 (km/h)

Thì vận tốc xe thứ hai là 60 – 10 = 50(km/h)

Câu 2:

Bạn Linh đi xe đạp từ nhà đến trường với quãng đường 10 km. Khi đi từ trường về nhà, vẫn trên cung đường ấy, do lượng xe tham gia giao thông nhiều hơn nên bạn Linh phải giảm vận tốc 2 km/h so với khi đến trường. Vì vậy thời gian về nhà nhiều hơn thời gian đến trường là 15 phút. Tính vận tốc của xe đạp khi bạn Linh đi từ nhà đến trường.

Xem đáp án

Gọi vận tốc của xe đạp khi bạn Linh đi từ nhà đến trường là x (km/h) $(x > 2)$ .

Thời gian để bạn Linh đi từ nhà đến trường là $\frac{10}{x}$ (giờ).

Vận tốc của xe đạp khi bạn Linh đi từ trường về nhà là $x - 2$ (km/h).

Do đó thời gian bạn Linh đi từ trường về nhà là $\frac{10}{x - 2}$ (giờ).

Theo bài ra, ta có phương trình $\frac{10}{x - 2} - \frac{10}{x} = \frac{1}{4}$

$\begin{array}{l} \Rightarrow 40 x - 40 (x - 2) = x (x - 2) \\ \Leftrightarrow x^{2} - 2 x - 80 = 0 \end{array}$ $\Leftrightarrow [\begin{array}{l} x = - 8 \\ x = 10 \end{array}$ .

Nhận xét : $x = - 8$ loại, $x = 10$ thỏa mãn.

Vậy vận tốc của xe đạp khi bạn Linh đi từ nhà đến trường là 10 km/h.

Câu 3:

Quãng đường từ A đến B dài 60 km. Một ca nô xuôi dòng từ A đến B rồi ngược dòng từ B về A mất tổng cộng 8h. Tính vận tốc thực của ca nô, biết vận tốc dòng nước là 4 km/ h

Xem đáp án

Quãng đường từ A đến B dài 60 km. Một ca nô xuôi dòng từ A đến B rồi ngược dòng từ B về A mất tổng cộng 8h. Tính vận tốc thực của ca nô, biết vận tốc dòng nước là 4 km/ h (ảnh 1)

Câu 4:

Nhân dịp Tết Thiếu nhi 01/6, một nhóm học sinh cần chia đều một số lượng quyển vở thành các phần quà để tặng cho các em nhỏ tại một mái ấm tình thương. Nếu mỗi phần quà giảm quyển thì các em sẽ có thêm phần quà nữa, còn nếu mỗi phần quà giảm quyển thì các em sẽ có thêm phần quà nữa. Hỏi ban đầu có bao nhiêu phần quà và mỗi phần quà có bao nhiêu quyển vở.

Xem đáp án

Gọi là số quyển vở của mỗi phần quà và là số phần quà dự tính ban đầu $(x, y \in ℕ^{*})$ .

Số quyển vở mà nhóm học sinh có là quyển vở.

Nếu mỗi phần quà giảm 2 quyển thì các em sẽ có thêm phần quà nên $(x - 2) (y + 2) = x y$ .

Nếu mỗi phần quà giảm 4 quyển thì các em sẽ có thêm phần quà nên $(x - 4) (y + 5) = x y$ .

Ta có hệ phương trình

$\{\begin{cases} (x - 2) (y + 2) = x y \\ (x - 4) (y + 5) = x y \end{cases} \Leftrightarrow \{\begin{cases} x - y = 2 \\ 5 x - 4 y = 20 \end{cases} \Leftrightarrow \{\begin{cases} 4 x - 4 y = 8 \\ 5 x - 4 y = 20 \end{cases} \Leftrightarrow \{\begin{cases} x = 12 \\ y = 10 \end{cases}$ (thỏa mãn).

Vậy có phần quà và mỗi phần quà có 12 quyển vở.

Câu 5:

Từ bến sông A một chiếc bè trôi về bến B với vận tốc dòng nước là 4 km/h, cùng lúc đó một chiếc thuyền chạy từ A đến B rồi quay lại thì gặp chiếc bè tại điểm cách bến A 8 km. Tính vận tốc thực của thuyền biết khoảng cách từ bến A đến B là 24 km.

Xem đáp án

Gọi vận tốc thực của chiếc thuyền là $x (k m / h), (x > 4)$ . Khi đó vận tốc của thuyền khi xuôi dòng từ A đến B là: $x + 4 (k m / h)$ ; ngược lại từ B về A thì thuyền đi với vận tốc là: $x - 4 (k m / h)$ .

Thời gian thuyền đi từ A đến B là $\frac{24}{x + 4} (h)$

Gọi C là vị trí thuyền và bè gặp nhau.

Vì nên thời gian thuyền từ B quay lại C là: $\frac{16}{x - 4} (h)$

Thời gian bè trôi với vận tốc dòng nước từ A đến C là $\frac{8}{4} = 2 (h)$ .

Vì thuyền và bè gặp nhau tại C nên ta có phương trình: $\frac{24}{x + 4} + \frac{16}{x - 4} = 2$

$\Leftrightarrow x^{2} - 20 x = 0 \Rightarrow x_{1} = 0 (l o a i); x_{2} = 20 (t / m)$

Vậy vận tốc thực của chiếc thuyền là: $20 (k m / h)$

Câu 6:

Một xe ô tô và xe máy khởi hành cùng một lúc từ địa điểm A đi đến địa điểm B cách nhau 60 km với vận tốc không đổi, biết vận tốc xe ô tô lớn hơn vận tốc xe máy là 20km/h và xe ô tô đến B sớm hơn xe máy là 30 phút. Tính vận tốc của mỗi xe.

Xem đáp án

Gọi vận tốc của xe máy là $x (k m / h)$ . ĐK $x > 0$

Vận tốc của xe ô tô là $x + 20 (k m / h)$ .

Thời gian xe máy đi từ A đến B là: $\frac{60}{x} (h)$

Thời gian xe ô tô đi từ A đến B là: $\frac{60}{x + 20} (h)$

Vì xe ô tô đến B sớm hơn xe máy là $30 phút = \frac{1}{2} h$ nên ta có phương trình

$\frac{60}{x} - \frac{60}{x + 20} = \frac{1}{2} \Rightarrow 120 (x + 20) - 120 x = x (x + 20)$

$\Rightarrow 120 x + 2400 - 120 x = x^{2} + 20 x \Rightarrow x^{2} + 20 x - 2400 = 0$

$\Rightarrow x^{2} + 20 x - 2400 = 0$

$Δ' = 100 + 2400 = 2500 > 0 \Rightarrow \sqrt{Δ'} = \sqrt{2500} = 50$

Phương trình có hai nghiệm

$x_{1} = - 10 + 50 = 40$ (t/m đk)

$x_{2} = - 10 - 50 = - 60$ (không t/m đk)

Vậy vận tốc của xe máy là $40 k m / h$ .

Vận tốc của xe ô tô là $40 + 20 = 60 (k m / h)$ .

Câu 7:

Để chuẩn bị cho mùa giải sắp tới, một vận động viên đua xe đạp ở Đồng Tháp đã luyện tập leo dốc và đổ dốc trên cầu Cao Lãnh. Biết rằng đoạn leo dốc và đổ dốc ở hai bên cầu có độ dài cùng bằng km. Trong một lần luyện tập, vận tốc của vận động viên khi đổ dốc nhanh hơn vận tốc khi leo dốc là km/h và tổng thời gian hoàn thành là phút. Tính vận tốc leo dốc của vận động viên trong lần luyện tập đó.

Xem đáp án

Gọi (km/h) (với $x > 0$ ) là vận tốc của vận động viên khi leo dốc. Khi đó (km/h) là vận tốc của vận động viên khi đổ dốc.

Vì tổng thời gian hoàn thành là $3 phút = \frac{1}{20}$ giờ nên ta có phương trình

$\frac{1}{x} + \frac{1}{x + 9} = \frac{1}{20} \Leftrightarrow 20 (x + 9) + 20 x = x (x + 9)$

$\Leftrightarrow x^{2} - 31 x - 180 = 0 \Leftrightarrow [\begin{array}{l} x = 36 \\ x = - 5 \end{array} \begin{matrix} (n) \\ (l) \end{matrix}$

Vậy vận tốc leo dốc của vận động viên trong lần luyện tập đó là 36 km/h.

Câu 8:

Một mảnh vườn hình chữ nhật có chiều dài hơn chiều rộng 5m. Nếu tăng chiều dài thêm 10m, tăng chiều rộng thêm 5m thì diện tích mảnh vườn đó tăng gấp đôi. Tính chiều dài và chiều rộng của mảnh vườn đó.

Xem đáp án

$\begin{array}{l} (x + 10) (x - 5 + 5) = 2 x (x - 5) \\ \Leftrightarrow (x + 10) . x = 2 x^{2} - 10 x \Leftrightarrow x^{2} + 10 x = 2 x^{2} - 10 x \\ \Leftrightarrow x^{2} - 20 x = 0 \Leftrightarrow [\begin{array}{l} x = 20 \\ x = 0 \end{array} \end{array}$

Câu 9:

Quãng đường dài 160 km. Hai xe khởi hành cùng một lúc từ A để đi đến B. Vận tốc của xe thứ nhất lớn hơn vận tốc của xe thứ hai là 10 km/h nên xe thứ nhất đến B sớm hơn xe thứ hai là 48 phút. Tính vận tốc của xe thứ hai.

Xem đáp án

Gọi vận tốc của xe thứ hai là x (km/h). Điều kiện: $x > 0$ ., vận tốc của xe thứ nhất là $x + 10$ (km/h).

Thời gian đi quãng đường của xe thứ nhất là $\frac{160}{x + 10}$ (h) và thời gian của xe thứ hai là $\frac{160}{x}$ (h).

Theo đề bài ta có phương trình $\frac{160}{x} - \frac{160}{x + 10} = \frac{48}{60}$

Giải phương trình ta được: $x = 40$ (nhận), $x = - 50$ (loại).

Vậy vận tốc của xe thứ hai là 40 km/h.

Câu 10:

Một mảnh đất hình chữ nhật có chu vi bằng 28 mét và độ dài đường chéo bằng 10 mét. Tính chiều dài và chiều rộng của mảnh đất đó theo đơn vị mét.

Xem đáp án

Nửa chu vi là: 28 : 2 = 14 (m)

Gọi chiều dài mảnh đất là x (mét). Điều kiện: 0 < x < 14.

=> Chiều rộng mảnh đất là 14 – x (mét).

Ta có chiều dài lớn hơn chiều rộng nên x > 14 – x => x > 7.

Vì độ dài đường chéo là 10 mét nên ta có phương trình

x² + (14 – x)² = 10²

Û 2x² – 28x + 196 = 100

Û x² – 14x + 48 = 0

Û $[\begin{array}{l} x = 8 > 7 (T M) \\ x = 6 < 7 (L) \end{array}$

Vậy chiều dài mảnh đất là 8 mét, chiều rộng là 14 – 8 = 6 (mét).

Câu 11:

Siêu thị A thực hiện chương trình giảm giá cho khách hàng mua loại túi bột giặt 4 kg như sau: Nếu mua 1 túi thì được giảm giá 10.000 đồng so với giá niêm yết. Nếu mua 2 túi thì túi thứ nhất được giảm 10.000 đồng và túi thứ hai được giảm 20.000 đồng so với giá niêm yết. Nếu mua từ túi thứ 3 trở lên thì ngoài 2 tú đầu được giảm giá như trên, từ túi thứ ba trở đi, mỗi tú sẽ được giảm 20% so với giá niêm yết.

a) Bà Tư mua 5 túi bột giặt loại 4 kg ở siêu thị A thì phải trả số tiền là bao nhiêu, biết rằng loại túi bột giặt mà bà Tư mau có giá niêm yết là 150 000 đồng/ túi.

b) Siêu thị B có hình thức giảm giá khác cho loại túi bột giặt như trên là: nếu mua từ 3 túi trở lên thì sẽ giảm giá 15% cho mỗi túi. Nếu bà Tư mua 5 túi bột giặt thì bà Tư nên mua ở siêu thị nào để số tiền phải trả ít hơn? Biết rằng giá niêm yết của hai siêu thị là như nhau.

Xem đáp án

a) Số tiền bà tư phải mua bột giặt ở Siêu thị A là:

$140 000 + 130 000 + 3. 150 000. 80 % = 630 000$ (đồng)

b) Số tiền nếu bà tư mua 5 túi bột giặt ở siêu thị B là:

150 000 . 80% . 5 = 637 500 (đồng)

Vậy bà Tư nên mua bột giặt ở siêu thị A sẽ trả ít tiền hơn.

Câu 12:

Nhiệt độ sôi của nước không phải lúc nào cũng 100⁰C mà phụ thuộc vào độ cao của nơi đó so với mực nước biển. Chẳng hạn Thành phố Hồ Chí Minh có độ cao xem ngang như mực nước biển (x = 0 m) thì nước có nhiệt độ sôi là y = 100⁰C nhưng ở thủ đô La Paz của Bolivia, Nam Mỹ có độ cao x = 3600 m so với mực nước biển thì nhiệt độ sối của nước là y = $87^{0} C$ . Ở độ cao trong khoảng vài km, người ta thấy mối liên hệ giữa hai đại lượng này là một hàm số bậc nhất y=ax+b có đồ thị như sau

Nhiệt độ sôi của nước không phải lúc nào cũng 1000C mà phụ thuộc vào độ cao của nơi đó so với mực nước biển. Chẳng hạn Thành phố Hồ Chí Minh có độ cao xem ngang như mực nước biển (x = 0 m) thì nước có nhiệt độ sôi là y = 1000C nhưng ở thủ đô La Paz của Bolivia, Nam Mỹ có độ cao x = 3600 m so với mực nước biển thì nhiệt độ sối của nước là y = . Ở độ cao trong khoảng vài km, người ta thấy mối liên hệ giữa hai đại lượng này là một hàm số bậc nhất y=ax+b có đồ thị như sau (ảnh 1)

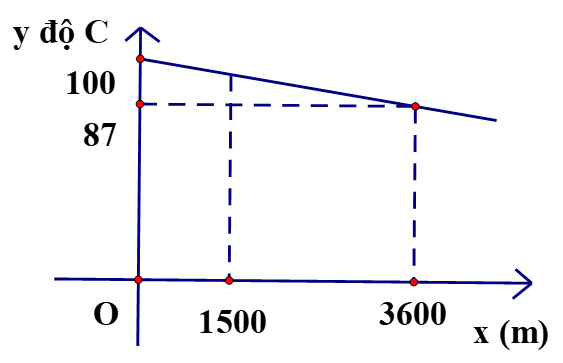
a) Xác định các hệ số a và b

b) Thành phố Đà Lạt có độ cao 1500m so với mực nước biển. Hỏi nhiệt độ sôi của nước ở Thành phố này là bao nhiêu

Xem đáp án

a) Xác định hệ số a và b

Ta có hàm số bậc nhất cần tìm có dạng y=ax+b

Theo đồ thị Oxy ta có hệ phương trình

$\{\begin{cases} 87 = a .3600 + b \\ 100 = a .0 + b \end{cases} \Leftrightarrow \{\begin{cases} a = \frac{- 13}{3600} \\ b = 100 \end{cases}$

b) Nhiệt độ sôi ở thành phố Đà Lạt là:

T=1500. $\frac{- 13}{3600}$ +100 $\approx 94,6 (° C)$