5 câu hỏi trắc nghiệm thuộc Đề thi Học kì 2 Toán 9 chọn lọc, có đáp án (Đề 5)

Câu 1:

Cho hàm số y = $- \frac{1}{2}$ x² có đồ thị (P) và hàm số y = x – 4 có đồ thị (D).

a) Vẽ (P) và (D) trên cùng hệ trục tọa độ.

b) Tìm tọa độ giao điểm của (P) và (D) bằng phép toán.

Xem đáp án

a)

• Vẽ (P): y = x²

Bảng giá trị

x	−2	−1	0	1	2
y = $- \frac{1}{2} x^{2}$	−2	−	0	−	−2

Do đó (P) là đồ thị đi qua các điểm:

A(−2; –2); $B (- 1; - \frac{1}{2})$ ; O(0; 0); $C (1; - \frac{1}{2})$ ; D(2; –2).

•Vẽ (D): y = x – 4

Đường thẳng (D): y = x – 4 có a = 1, b = −4 đi qua 2 điểm M(0; b) và N $(\frac{- b}{a}; 0)$

Do đó 2 điểm thuộc đường thẳng (D) là M(0;−4) và N(4;0).

Ta vẽ được (P) và (D) như hình vẽ sau:

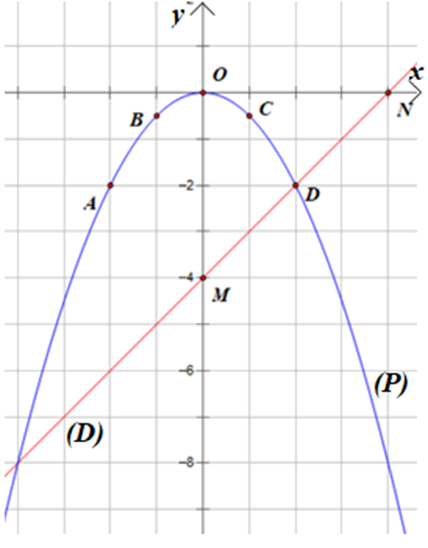
Cho hàm số y = x2 có đồ thị (P) và hàm số y = x – 4 có đồ thị (D). a) Vẽ (P) và (D) trên cùng hệ trục tọa độ. b) Tìm tọa độ giao điểm của (P) và (D) bằng phép toán. (ảnh 1)

b) Phương trình hoành độ giao điểm của (P) và (D) là:

$- \frac{1}{2}$ x² = x – 4

Û −x² = 2x – 8

Û −x² – 2x + 8 = 0

Û x² + 2x – 8 = 0

Û x² – 2x + 4x – 8 = 0

Û x(x – 2) + 4(x – 2) = 0

Û (x – 2)(x + 4) = 0

Û $[\begin{matrix} x - 2 = 0 \\ x + 4 = 0 \end{matrix}$ Û $[\begin{matrix} x = 2 \\ x = - 4 \end{matrix}$

• Thay x = 2 vào phương trình của (D): y = x – 4 ta được:

y = 2 – 4 = −2

Ta có tọa độ giao điểm (2; −2).

• Thay x = −4 vào phương trình của (D): y = x – 4 ta được:

y = −4 − 4 = −8

Ta có tọa độ giao điểm (−4; −8).

Vậy tọa độ giao điểm của (P) và (D) là (2; −2) và (−4; −8).

Câu 2:

Giải bài toán bằng cách lập hệ phương trình:

Trong kỳ thi học kì I môn toán lớp 9, một phòng thi của trường có 24 thí sinh dự thi. Các thí sinh đều phải làm bài trên giấy thi của trường phát cho, cuối buổi thi, sau khi thu bài, giám thị coi thi đếm được tổng số tờ là 59 tờ giấy thi. Hỏi trong phòng thi có bao nhiêu thí sinh làm bài 2 tờ giấy thi, bao nhiêu thí sinh làm bài 3 tờ giấy thi? Biết rằng có 3 thí sinh chỉ làm 1 tờ giấy thi.

Xem đáp án

Gọi số học sinh làm bài 2 tờ giấy thi là x (x ∈ ℕ*) (học sinh)

Số học sinh làm bài 3 tờ giấy thi là y (y ∈ ℕ*) (học sinh)

Vì có 24 thí sinh dự thi mà có 3 thí sinh làm 1 tờ giấy thi nên ta có phương trình:

x + y + 3 = 24

Û x + y = 21 (1)

Vì tổng số tờ giấy thi là 59 tờ và có 3 thí sinh làm 1 tờ giấy thi nên ta có phương trình:

2x + 3y + 3 = 59

Û 2x + 3y = 56 (2)

Từ (1) và (2), ta có hệ phương trình:

$\{\begin{matrix} x + y = 21 \\ 2 x + 3 y = 56 \end{matrix}$

Û $\{\begin{matrix} 2 x + 2 y = 42 \\ 2 x + 3 y = 56 \end{matrix}$

Û $\{\begin{matrix} y = 14 \\ 2 x + 3.14 = 56 \end{matrix}$

Û $\{\begin{matrix} y = 14 \\ x = 7 \end{matrix}$ (thỏa mãn)

Vậy có 7 thí sinh làm bài 2 tờ giấy thi và có 14 thí sinh làm 3 tờ giấy thi.

Câu 3:

Công ty A thực hiện một cuộc khảo sát để tìm hiểu về mối liên hệ giữa y (sản phẩm) là số lượng sản phẩm T bán ra với x (đồng) là giá bán ra của mỗi sản phẩm T và nhận thấy rằng y = ax + b (a, b là hằng số). Biết giá bán là 500 000 đồng một sản phẩm thì số lượng sản phẩm bán ra là 1 300 (sản phẩm); với giá bán 540 000 đồng một sản phẩm thì số lượng sản phẩm bán ra là 1 600 (sản phẩm).

a) Xác định a, b.

b) Bằng phép tính, hãy tính số lượng sản phẩm bán ra với giá bán là 480 000 đồng một sản phẩm?

Xem đáp án

Ta có: số lượng sản phẩm T bán ra với x (đồng) là giá bán ra của mỗi sản phẩm T và nhận thấy rằng y = ax + b (a, b là hằng số).

Với giá bán là 500 000 đồng một sản phẩm thì số lượng sản phẩm bán ra là 1 300 (sản phẩm) thì ta có: 1 300 = a.500 000 + b.

Với giá bán 540 000 đồng một sản phẩm thì số lượng sản phẩm bán ra là 1 600 (sản phẩm) thì ta có: 1 600 = a.540 000 + b

Ta lập được hệ phương trình:

$\{\begin{cases} 1 300 = a .500 000 + b \\ 1 600 = a .540 000 + b \end{cases}$

Û $\{\begin{matrix} 1 300 = a .500 000 + b \\ 40 000 a = 300 \end{matrix}$

$\Leftrightarrow \{\begin{matrix} 1 300 = 0, 0075.500 000 + b \\ a = 0, 0075 \end{matrix}$

$\Leftrightarrow \{\begin{matrix} b = - 2450 \\ a = 0, 0075 \end{matrix}$

b) Với a = 0,0075 và b = –2450 ta có:

y = 0,0075x – 2450.

Số sản phẩm bán được với giá bán là 480 000 đồng là:

y = 0,0075.480 000 – 2450 = 1 150 (sản phẩm)

Vậy với giá 480 000 đồng một sản phẩm thì bán ra được 1 150 sản phẩm.

Câu 4:

Người ta thả một quả trứng vào cốc thủy tinh hình trụ có chứa nước, trứng chìm hoàn toàn xuống đáy cốc. Hỏi thể tích quả trứng dó là bao nhiêu cm³? (làm tròn đến hàng đơn vị). Biết cốc thủy hình trụ có đường kính đáy 10 cm và nước trong cốc dâng thêm 7,5 mm.

(Công thức tính thể tích hình trụ: V = pr²h, với r là bán kính đáy và h là chiều cao của hình trụ.)

Xem đáp án

Đổi 7,5 mm = 0,75 cm.

R = $\frac{d}{2}$ = $\frac{10}{2}$ = 5 cm.

Ta có thể tích của quả trứng chính là thể tích phần nước dâng lên.

Thể tích quả trứng là khoảng:

V = pr²h = p.5².0,75 ≈ 59 (cm³)

Vậy thể tích của quả trứng là khoảng 59 cm³.

Câu 5:

Cho ∆ABC nhọn (AB < AC) nội tiếp đường tròn (O) và 2 đường cao BD, CE cắt nhau tại H (D Î AC, E Î AB).

a) Chứng minh tứ giác BEDC nội tiếp.

b) Vẽ đường kính AM của đường tròn (O), AH cắt BC tại F (F Î BC).

Chứng minh: AB.AC = AF.AM

c) Tia DE và CB cắt nhau tại K. AK cắt đường tròn (O) tại N. Chứng minh: N, H, M thẳng hàng.

Xem đáp án

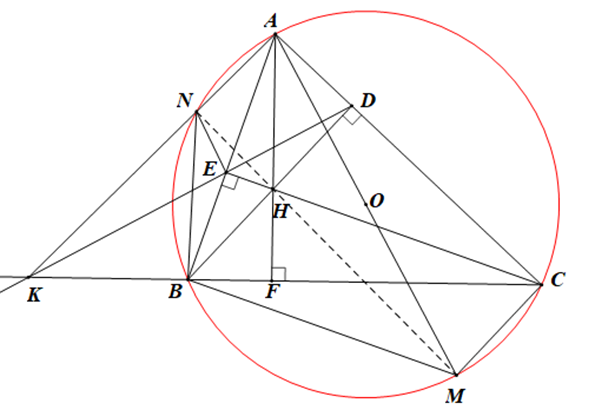
Cho ∆ABC nhọn (AB < AC) nội tiếp đường tròn (O) và 2 đường cao BD, CE cắt nhau tại H (D  AC, E  AB). a) Chứng minh tứ giác BEDC nội tiếp. b) Vẽ đường kính AM của đường tròn (O), AH cắt BC tại F (F  BC). Chứng minh: AB.AC = AF.AM c) Tia DE và CB cắt nhau tại K. AK cắt đường tròn (O) tại N. Chứng minh: N, H, M thẳng hàng. (ảnh 1)

a) Ta có: $\hat{B E C}$ = 90° (CE ^ AB), $\hat{B D C}$ = 90° (BD ^ AC)

Þ $\hat{B E C} = \hat{B D C}$ = 90°

Mà $\hat{B E C}$ và $\hat{B D C}$ là hai góc có đỉnh kề nhau cùng nhìn cạnh BC của tứ giác BEDC.

Þ Tứ giác BEDC nội tiếp.

b) Ta có điểm C nằm trên đường tròn (O) đường kính AM

Nên $\hat{A C M}$ = 90° (góc nội tiếp chắn nửa đường tròn)

Mà AH cắt BC tại F nên AF ⊥ BC do đó $\hat{A F B} = 90 °$

Suy ra $\hat{A C M} = \hat{A F B}$ = 90°

Xét ∆ACM và ∆ABF, có:

$\hat{A C M} = \hat{A F B}$ = 90° (chứng minh trên),

$\hat{A B C} = \hat{A M C}$ (hai góc nội tiếp cùng chắn cung AC của (O))

Þ ∆ACM ᔕ ∆AFB (g.g)

Þ $\frac{A C}{A F} = \frac{A M}{A B}$ (tỉ số đồng dạng)

Þ AB.AC = AF.AM (đpcm).

c) • Tứ giác BEDC là tứ giác nội tiếp (chứng minh câu a)

Þ $\hat{E D C} = \hat{E C B}$ (hai góc nội tiếp cùng chắn cung EB)

Hay $\hat{K D B} = \hat{K C E}$

Xét DKDB và DKCE có:

$\hat{K D B} = \hat{K C E}$ (Chứng minh trên),

$\hat{D K C}$ là góc chung

Þ DKDB ᔕ DKCE (g.g)

$\Rightarrow \frac{K D}{K C} = \frac{K B}{K E}$ (tỉ số đồng dạng)

Þ KB.KC = KD.KE (1)

• Tứ giác ANBC nội tiếp

$\Rightarrow \hat{K B N} = \hat{K A C}$

Xét DKBN và DKAC có:

$\hat{A K C}$ là góc chung,

$\hat{K B N} = \hat{K A C}$ (chứng minh trên)

Þ DKBN ᔕ DKAC (g.g)

$\Rightarrow \frac{K B}{K A} = \frac{K N}{K C}$ (tỉ số đồng dạng)

Þ KB. KC = KA.KN (2)

Từ (1) và (2) ta có:

KD.KE = KA.KN (= KB. KC)

$\Rightarrow \frac{K E}{K A} = \frac{K N}{K D}$

Xét DKNE và DKAD có:

$\hat{A K D}$ là góc chung,

$\frac{K E}{K A} = \frac{K N}{K D}$ (chứng minh trên)

Þ DKNE ᔕ DKAD (c.g.c)

$\Rightarrow \hat{K E N} = \hat{K A D}$ (hai góc tương ứng)

Þ Tứ giác ANED nội tiếp đường tròn.

Do đó 4 điểm A, N, E, D cùng thuộc một đường tròn (3)

• Tứ giác AEHD có $\hat{A E H} = \hat{A D H} (= 90 °)$

Þ E và D cùng thuộc đường tròn đường kính AH

Þ 4 điểm A, E, H, D cùng thuộc đường tròn đường kính AH (4)

Từ (3) và (4) suy ra 5 điểm A, N, E, H, D cùng thuộc đường tròn đường kính AH

Do đó tứ giác ANHD nội tiếp đường tròn

$\Rightarrow \hat{A N H} = 90 °$ (góc nội tiếp chắn nửa đường tròn)

Þ AN ⊥ HN tại N (5)

• Ta có điểm N nằm trên đường tròn đường kính AM

$\Rightarrow \hat{A N M}$ = 90° (góc nội tiếp chắn nửa đường tròn)

Þ AN ⊥ MN tại N (6)

Từ (5) và (6) ta có: MN ≡ HN

Do đó ba điểm N, H, M thẳng hàng.