7 câu hỏi trắc nghiệm thuộc Đề thi Học kì 2 Toán 9 chọn lọc, có đáp án (Đề 6)

Câu 1:

(1,5 điểm) Giải các phương trình

a) 2x² – 5x + 2 = 0;

b) x⁴ + x² – 6 = 0.

Xem đáp án

a) 2x² – 5x + 2 = 0

Cách 1:

Ta có D = (–5)² – 4.2.2 = 9 > 0

Khi đó phương trình đã cho có hai nghiệm phân biệt

$x_{1} = \frac{5 + \sqrt{9}}{2.2} = 2$ và $x_{2} = \frac{5 - \sqrt{9}}{2.2} = \frac{1}{2}$

Vậy phương trình đã cho có tập nghiệp $S = \{2; \frac{1}{2}\}$

Cách 2:

2x² – 5x + 2 = 0

Û x² − $\frac{5}{2}$ x + 1 = 0

Û x² − $\frac{1}{2}$ x – 2x + 1 = 0

Û x $(x - \frac{1}{2})$ − 2 $(x - \frac{1}{2})$ = 0

Û (x – 2) $(x - \frac{1}{2})$ = 0

Û $[\begin{matrix} x - 2 = 0 \\ x - \frac{1}{2} = 0 \end{matrix}$ Û $[\begin{matrix} x = 2 \\ x = \frac{1}{2} \end{matrix}$ .

Vậy phương trình đã cho có tập nghiệp $S = \{2; \frac{1}{2}\}$

b) x⁴ + x² – 6 = 0 (1)

Đặt t = x² (t ≥ 0), phương trình (1) trở thành:

t² + t – 6 = 0 (2)

Ta có hai cách giải phương trình (2) như sau:

Cách 1:

Ta có D = 1² – 4.1.(–6) = 25 > 0

Khi đó phương trình đã cho có hai nghiệm phân biệt là:

$t_{1} = \frac{- 1 + \sqrt{25}}{2.1} = 2$ (thỏa mãn) và $t_{2} = \frac{- 1 - \sqrt{25}}{2.1} = - 3$ (không thỏa mãn)

Cách 2:

t² + t – 6 = 0 (2)

Û t² – 2t + 3t – 6 = 0

Û t(t – 2) + 3(t – 2) = 0

Û (t – 2)(t + 3) = 0

Û $[\begin{matrix} t - 2 = 0 \\ t + 3 = 0 \end{matrix}$

Û t = 2 (thỏa mãn) hay t = −3 (không thỏa mãn).

Với t = 2, ta có: x² = 2

Û x = $\sqrt{2}$ hoặc x = $- \sqrt{2}$ .

Vậy phương trình đã cho có tập nghiệm $S = \{\sqrt{2}; - \sqrt{2}\} .$

Câu 2:

(1,5 điểm)

a) Vẽ đồ thị (P) của hàm số y = $\frac{x^{2}}{2}$ và đồ thị (D) của hàm số y = −3x – 4 trên cùng hệ trục tọa độ.

b) Tính tọa độ các giao điểm của đồ thị (P) và đồ thị (D).

Xem đáp án

+ Vẽ (P): y = $\frac{x^{2}}{2}$

Bảng giá trị

x	−2	−1	0	1	2
y = $\frac{x^{2}}{2}$	2	$\frac{1}{2}$	0	$\frac{1}{2}$	2

Do đó (P) là đồ thị đi qua các điểm:

A(−2; 2); $B (- 1; \frac{1}{2})$ ; O(0; 0); $C (1; \frac{1}{2})$ ; D(2; 2).

+ Vẽ (D): y = −3x – 4

Đường thẳng (D): y = −3x – 4 có a = −3, b = −4 đi qua 2 điểm M(0; b) và N $(\frac{- b}{a}; 0)$

Do đó 2 điểm thuộc đường thẳng (D) là M(0;−4) và N $(\frac{- 4}{3}; 0)$

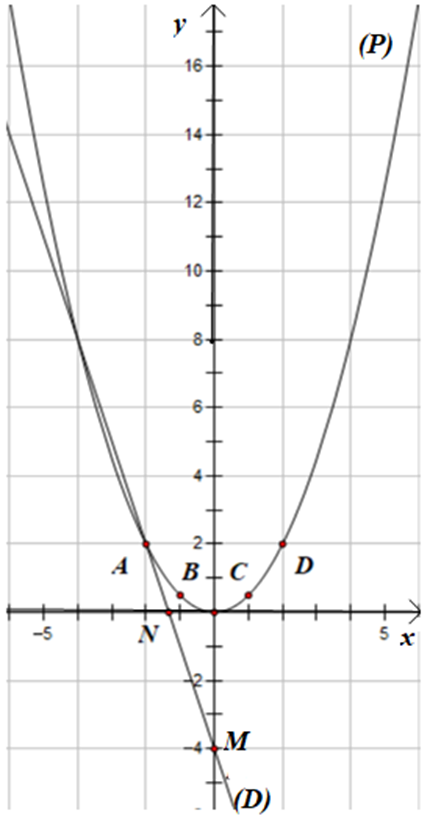
a) Vẽ đồ thị (P) của hàm số y = và đồ thị (D) của hàm số y = −3x – 4 trên cùng hệ trục tọa độ. b) Tính tọa độ các giao điểm của đồ thị (P) và đồ thị (D). (ảnh 1)

b) Phương trình hoành độ giao điểm của (P) và (D) là:

$\frac{1}{2}$ x² = −3x – 4

Û x² = –6x – 8

Û x² + 6x + 8 = 0

Û x² + 4x + 2x + 8 = 0

Û x(x + 4) + 2(x + 4) = 0

Û (x + 4)(x + 2) = 0

Û $[\begin{matrix} x + 4 = 0 \\ x + 2 = 0 \end{matrix}$

Û $[\begin{matrix} x = - 2 \\ x = - 4 \end{matrix}$

• Thay x = −2 vào phương trình của (D): y = −3x – 4 ta được:

y = −3.(−2) − 4 = 2

Ta có tọa độ giao điểm là (−2; 2).

• Thay x = −4 vào phương trình của (D): y = −3x – 4 ta được:

y = −3.(−4) − 4 = 8

Ta có tọa độ giao điểm là (−4; 8).

Vậy tọa độ các giao điểm của (P) và (D) là (−2; 2) và (−4; 8).

Câu 3:

(1,5 điểm) Cho phương trình: x² + 2mx + m² + 2m – 2 = 0 (1) (x là ẩn).

a) Tìm giá trị của m để phương trình (1) có hai nghiệm.

b) Gọi x₁, x₂ là hai nghiệm của phương trình (1). Tìm giá trị của m để x₁x₂ + x₁ + x₂ = 0.

Xem đáp án

x² + 2mx + m² + 2m – 2 = 0 có a = 1, b = 2m, c = m² + 2m – 2

Ta có:

∆ = b² – 4ac

= (2m)² – 4.1.(m² + 2m – 2)

= -8m + 8

a) Để phương trình (1) có hai nghiệm Û ∆ ≥ 0

Û −8m + 8 ≥ 0 Û m ≤ 1.

Vậy với m ≤ 1 thì phương trình (1) có hai nghiệm.

b) Với m ≤ 1, phương trình (1) có hai nghiệm x₁, x₂

Theo hệ thức Vi – ét ta có:

$\{\begin{matrix} x_{1} + x_{2} = \frac{- b}{a} = - 2 m \\ x_{1} x_{2} = \frac{c}{a} = m^{2} + 2 m - 2 \end{matrix}$

Ta có: x₁x₂ + x₁ + x₂ = 0

Û m² + 2m – 2 – 2m = 0

Û m² = 2

Û m = $\sqrt{2}$ (không thỏa mãn) hoặc m = $- \sqrt{2}$ (thỏa mãn)

Vậy m = $- \sqrt{2}$ thỏa mãn yêu cầu bài toán.

Câu 4:

(1,0 điểm) Lớp 9A có 42 học sinh. Vừa qua lớp đã phát động phong trào tặng sách cho các bạn khó khăn ở vùng sâu. Tại buổi phát động, mỗi học sinh trong lớp đều tặng 3 quyển sách hoặc 5 quyển sách. Kết quả cả lớp đã tặng được 146 quyển sách. Hỏi lớp 9A có bao nhiêu bạn tặng 3 quyển sách và bao nhiêu bạn tặng 5 quyển sách?

Xem đáp án

Gọi số học sinh tặng 3 quyển sách của lớp 9A là x (x ∈ ℕ*) (bạn).

Số học sinh tặng 5 quyển sách của lớp 9A là y (y ∈ ℕ*) (bạn).

Vì lớp 9A có 42 học sinh nên ta có phương trình: x + y = 42 (1)

Vì cả lớp 9A đã tặng được 146 quyển sách nên ta có phương trình:

3x + 5y = 146 (2)

Từ (1) và (2), ta có hệ phương trình:

Û $\{\begin{matrix} x + y = 42 \\ 3 x + 5 y = 146 \end{matrix}$

$\{\begin{matrix} 3 x + 3 y = 126 (3) \\ 3 x + 5 y = 146 (4) \end{matrix}$

Ta lấy phương trình (4) trừ phương trình (3) vế theo vế ta được phương trình:

2y = 20

Û y = 10 (thỏa mãn)

Thay y = 10 vào phương trình (1) ta được:

x + 10 = 42 Û x = 32 (thỏa mãn)

Vậy lớp 9A có 32 bạn tặng 3 quyển sách và 10 bạn tặng 5 quyển sách.

Câu 5:

(1,0 điểm) Một cửa hàng bán loại kem lạnh A như sau: nếu mua không quá 3 hộp thì giá 40 nghìn đồng mỗi hộp, nếu mua nhiều hơn 3 hộp thì bắt đầu từ hộp thứ tư trở đi giá mỗi hộp sẽ giảm đi 20% so với giá ban đầu.

a) Viết công thức tính y (số tiền mua kem) theo x (số hộp kem mua được trong trường hợp mua nhiều hơn 3 hộp).

b) An và Bình đều mua loại kem lạnh A với số hộp nhiều hơn 3. Biết rằng số hộp kem An mua gấp đôi số hộp Bình mua, đồng thời tổng số tiền mua kem của hai bạn là 624 nghìn đồng, hỏi bạn Bình mua bao nhiêu hộp kem? Giải thích.

Xem đáp án

a) Gọi y là số tiền mua kem (nghìn đồng) (y > 0).

x là số hộp kem mua được (hộp) (x > 3, x ∈ ℕ*).

Số tiền khi mua 3 hộp kem là:

3.40 = 120 (nghìn đồng)

Số hộp kem được tính với giá 20% là:

x – 3 (hộp kem)

Giá mỗi hộp kem (từ hộp thứ tư trở đi) là:

(100% – 20%).40 = 32 (nghìn đồng)

Số tiền cần trả khi mua nhiều hơn 3 hộp kem là:

y = 120 + (x – 3).32

= 32x + 24 (nghìn đồng).

b) Gọi a (hộp) là số hộp kem Bình mua (a > 3, a ∈ ℕ*)

Khi đó số hộp kem An mua là 2a (hộp kem)

Vì tổng số tiền mua kem của hai bạn là 624 nghìn đồng nên ta có phương trình:

32a + 24 + 32.2a + 24 = 624

Û 96a = 576 Û a = 6 (thỏa mãn).

Vậy Bình mua 6 hộp kem.

Câu 6:

(0,5 điểm) Từ một tấm tôn hình chữ nhật, kích thước 50cm x 189cm người ta cuộn tròn lại thành mặt xung quanh của một hình trụ cao 50 cm (như hình bên).

Hãy tính bán kính r của đường tròn đáy và thể tích của hình trụ (kết quả làm tròn đến hàng dơn vị). Biết: diện tích xung quanh của hình trụ bằng 2prh, thể tích hình trụ bằng pr²h (h là chiều cao của hình trụ).

Xem đáp án

Diện tích tấm tôn hình chữ nhật kích thước 50cm x 189cm là:

50 . 189 = 9450 (cm²)

Diện tích xung quanh của hình trụ được tính như sau:

S = 2prh

Mà tấm tôn hình chữ nhật cuộn tròn lại thành mặt xung quanh của một hình trụ cao 50 cm nên diện tích của tấm tôn chính là diện tích xung quang của hình trụ.

Do đó ta có: 2pr.50 = 9450

Þ 2pr = 189

Þ r = $\frac{189}{2 π}$ ≈ 30 (cm).

Vậy bán kính hình tròn đáy là khoảng 30 cm.

Thể tích hình trụ là:

V = pr².h ≈ p.30².50 ≈ 141 372 (cm³).

Câu 7:

(3,0 điểm) Cho đường tròn tâm O, bán kính R và điểm A ở ngoài đường tròn (O; R) sao cho AO > 2R. Kẻ 2 tiếp tuyến AB, AC (B, C là các tiếp điểm). Gọi H là giao điểm của AO và BC.

a) Chứng minh tứ giác ABOC nội tiếp và OH.OA = R².

b) Kẻ dây cung BD của đường tròn (O; R) song song với AO. Đoạn AD cắt (O; R) tại E (khác D). Gọi F là trung điểm của DE. Chứng minh tứ giác ABFO nội tiếp và tam giác BEF vuông.

c) Kẻ đường kính BK của đường tròn (O; R). Chứng minh tia AO là phân giác của góc DAK.

Xem đáp án

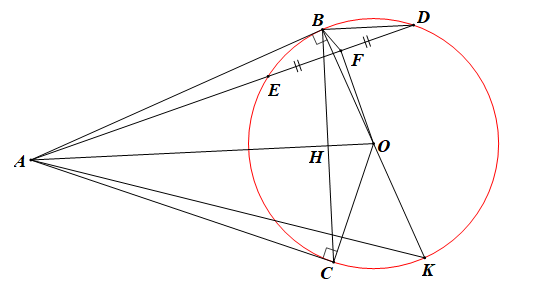
(3,0 điểm) Cho đường tròn tâm O, bán kính R và điểm A ở ngoài đường tròn (O; R) sao cho AO > 2R. Kẻ 2 tiếp tuyến AB, AC (B, C là các tiếp điểm). Gọi H là giao điểm của AO và BC. a) Chứng minh tứ giác ABOC nội tiếp và OH.OA = R2. b) Kẻ dây cung BD của đường tròn (O; R) song song với AO. Đoạn AD cắt (O; R) tại E (khác D). Gọi F là trung điểm của DE. (ảnh 1)

a) Ta có: AB, AC là 2 tiếp tuyến

Þ AB ^ OB; AC ^ OC

Xét tứ giác ABOC có $\hat{A B O} = \hat{A C O} = 90 °$

Þ Hai điểm B và C cùng nằm trên đường tròn đường kính AO

Þ Tứ giác ABOC nội tiếp đường tròn đường kính AO.

Vì AB, AC là hai tiếp tuyến của (O) cắt nhau tại A

Nên AB = AC và OB = OC (tính chất hai tiếp tuyến cắt nhau)

Suy ra A và O cùng nằm trên đường trung trực của BC

Do đó AO là đường trung trực của BC.

Þ AO ⊥ BC.

Xét ∆ABO vuông tại B ( $\hat{A B O} = 90 °$ ), BH ^ AO (BC ^ AO, H Î BC)

Theo hệ thức lượng trong tam giác vuông ta có:

OB² = OH.OA

Þ OH.OA = R².

b) F là trung điểm ED

Þ OF ^ ED (liên hệ giữa dây cung và đường kính)

Xét tứ giác ABFO có $\hat{A B O} = \hat{A F O} = 90 °$

Mà $\hat{A B O}$ và $\hat{A F O}$ là hai góc có đỉnh kề nhau của tứ giác ABFO

Þ Tứ giác ABFO nội tiếp

Þ $\hat{A F B} = \hat{A O B}$ (hai góc nội tiếp cùng chắn cung AB)

Mà $\hat{B E D} = \hat{B C D}$ (2 góc cùng chắn cung BD) và $\hat{B C D} = \hat{H B O}$ (Tam giác OBC cân tại O).

=> $\Rightarrow \hat{B E F} + \hat{B F E} = \hat{B C D} + \hat{B F A} = \hat{H B O} + \hat{B O H}$

Mà $\hat{H B O} + \hat{B O H} = 90 °$ (do ∆BHO vuông tại H).

Þ $\Rightarrow \hat{B E F} + \hat{B F E} = 90 °$

$\hat{E B F} = 90 °$

Þ Tam giác BEF vuông tại B.

c) Xét ∆ABO và ∆ACO có :

AO chung,

OB = OC = R,

$\hat{A B O} = \hat{A C O} = 90 °$

Þ ∆ABO = ∆ACO (cạnh huyền – cạnh góc vuông)

Þ $\hat{B A O} = \hat{C A O}$ (hai góc tương ứng)

Mà BD // AO Þ BD ^ BC

Þ $\hat{C B D} = 90 °$

Þ CD là đường kính của (O)

Xét ∆BDC và ∆CBK có:

CD = BK = 2R,

$\hat{B C K} = \hat{C B D} = 90 °$ ,

BC chung,

Þ ∆BDC = ∆CBK (cạnh huyền – cạnh góc vuông)

Þ BD = CK

Ta có: $\hat{A B D} = \hat{A B K} + \hat{K B D} = 90 ° + \hat{K B D} \hat{A C K} = \hat{A C D} + \hat{D C K} = 90 ° + \hat{D C K}$

Mà $\hat{K B D} = \hat{D C K}$ (hai góc nội tiếp cùng chắn cung DK)

$\Rightarrow \hat{A B D} = \hat{A C K}$

Xét ∆ABD và ∆ACK có:

AB = AC (chứng minh câu a),

$\hat{A B D} = \hat{A C K}$ (chứng minh trên),

BD = CK

Þ ∆ABD = ∆ACK (c.g.c)

Þ $\hat{B A D} = \hat{C A K}$ (hai góc tương ứng)

Tam giác ABC có AB = AC (chứng minh trên)

Nên DABC cân tại A

$\Rightarrow \hat{B A O} = \hat{C A O}$ (tính chất tam giác cân)

$\Rightarrow \hat{B A O} - \hat{B A D} = \hat{C A O} - \hat{C A K}$

=> $\hat{D A O} = \hat{K A O}$

Þ AO là phân giác góc DAK.

Vậy AO là phân giác góc DAK.