18 câu hỏi trắc nghiệm thuộc Bộ 15 đề kiểm tra học kì 1 Toán 9 năm 2022-2023 có đáp án (Đề 14)

Câu 1:

Biểu thức $\sqrt{1 - y^{2}}$ xác định khi và chỉ khi:

A. $y \leq 1$

B.

y \geq 1

C.

- 1 \leq y \leq 1

D.

y \neq 1.

Xem đáp án

Đáp án C

Phương pháp:

Biểu thức $\sqrt{A}$ xác định $\Leftrightarrow A \geq 0$

Cách giải:

$\sqrt{1 - y^{2}}$ xác định $\Leftrightarrow 1 - y^{2} \geq 0 \Leftrightarrow y^{2} \leq 1 \Leftrightarrow - 1 \leq y \leq 1$

Câu 2:

Rút gọn biểu thức

- \sqrt{18} + \sqrt{2}

được kết quả là:

A. $- 4$

B.

- \sqrt{20}

C.

- 2 \sqrt{2}

D.

- 4 \sqrt{2}

Xem đáp án

Đáp án C

Phương pháp:

Áp dụng quy tắc đưa thừa số ra ngoài dấu căn: $\sqrt{A^{2} . B} = |A| \sqrt{B} = [\begin{array}{l} A . B khi A \geq 0 \\ - A . B khi A < 0 \end{array}$

Cách giải:

$- \sqrt{18} + \sqrt{2} = - \sqrt{9.2} + \sqrt{2} = - \sqrt{3^{2} .2} + \sqrt{2} = - 3 \sqrt{2} + \sqrt{2} = - 2 \sqrt{2}$

Câu 3:

Hệ số góc của đường thẳng y=-2x-1 là:

A. -2

B. -1

C. 1

D. 2.

Xem đáp án

Đáp án A

Phương pháp:

Phương trình đường thẳng có dạng $y = k x + b$ có hệ số góc là k

Cách giải:

Phương trình đường thẳng $y = - 2 x - 1$ có hệ số góc là -2

Câu 4:

Góc tạo bởi đường thẳng nào sau đây với trục Ox là nhỏ nhất?

A. $y = - x + 4$

B.

y = x + 3

C.

y = 3 x + 2

D.

y = 5 x - 1.

Xem đáp án

Đáp án B

Phương pháp:

Đường thẳng $d : y = a x + b$ có hệ số góc $a \neq 0$ thì góc tạo bởi đường thẳng d và chiều dương của trục Ox sẽ:

+) Là góc nhọn nếu hệ số $a > 0,$ hệ số a càng lớn thì góc đó càng lớn (nhưng vẫn nhỏ hơn $90 °$ ).

+) Là góc tù nếu hệ số $a < 0,$ hệ số a càng nhỏ thì góc đó càng lớn (nhưng vẫn nhỏ hơn $180 °$ ).

Cách giải:

Trong 4 đáp án, ta có:

+) Đáp án A: đường thẳng $y = - x + 4$ có hệ số $a = - 1 < 0$

$\Rightarrow$ góc tạo bởi đường thẳng và trục $O x$ là góc tù.

+) Các đáp án B, C, D đều có hệ số $a > 0$ nên góc tạo bởi các đường thẳng $y = x + 3, y = 3 x + 2, y = 5 x - 1$ với trục Ox là các góc nhọn.

Đường thẳng $y = x + 3$ có hệ số $a = 1$ nhỏ nhất sẽ tạo với trục $O x$ góc nhỏ nhất.

Câu 5:

Biểu thức $\sqrt[3]{{(1 - \sqrt{2018})}^{3}} - \sqrt{2018}$ có giá trị bằng:

A. 1

B.

- 1

C.

1 - 2 \sqrt{2018}

D.

2 \sqrt{2018} - 1.

Xem đáp án

Đáp án C

Phương pháp:

Áp công thức: $\sqrt[3]{A^{3}} = A \forall A .$

Cách giải: $\sqrt[3]{{(1 - \sqrt{2018})}^{3}} - \sqrt{2018} = 1 - \sqrt{2018} - \sqrt{2018} = 1 - 2 \sqrt{2018} .$

Câu 6:

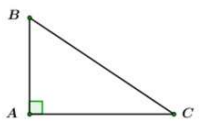
Tam giác ABC vuông tại A có AB=3cm, AC=4cm. Khi đó cosC có giá trị bằng:

A. $\frac{3}{4}$

B.

\frac{4}{3}

C.

\frac{3}{5}

D.

\frac{4}{5} .

Xem đáp án

Đáp án D

Phương pháp:

Áp dụng định lý Pytago trong tam giác $A B C$ vuông tại A:

$A B^{2} + A C^{2} = B C^{2}$ và $\cos C = \frac{A C}{B C} .$

Cách giải:

Ta có: $B C^{2} = A B^{2} + A C^{2} = 3^{2} + 4^{2} = 25 \Rightarrow B C = \sqrt{25} = 5 (c m)$

$\Rightarrow \cos C = \frac{A C}{B C} = \frac{4}{5} .$

Câu 7:

Biết $0^{0} < a < 90 ° .$ Giá trị của biểu thức $[\sin α + 3 \cos (90 ° - α)] : [\sin α - 2 \cos (90 ° - α)]$ bằng:

A. -4

B. 4

C.

\frac{- 3}{2}

D.

\frac{3}{2} .

Xem đáp án

Đáp án A

Phương pháp:

Áp dụng tính chất: $\sin α = \cos (90 ° - α); \cos α = \sin (90 ° - α) .$

Cách giải:

$[\sin α + 3 \cos (90 ° - α)] : [\sin α - 2 \cos (90 ° - α)] = (\sin α + 3 \sin α) : (\sin α - 2 \sin α) = (4 \sin α) : (- \sin α) = - 4.$

Câu 8:

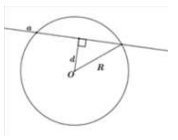
Đường thẳng $a$ cách tâm O của đường tròn $(O; R)$ một khoảng bằng $\sqrt{8} c m .$ Biết $R = 3 c m,$ số giao điểm của đường thẳng $a$ và đường tròn $(O; R)$ là:

A. 0

B. 1

C. 2

D. 3

Xem đáp án

Đáp án C

Phương pháp:

Vị trí tương đối của đường tròn tâm O bán kính R và đường thẳng $a$ :

+) Nếu $d (O; a) < R \Rightarrow a$ cắt đường tròn tại hai điểm phân biệt.

+) Nếu $d (O; a) = R \Rightarrow a$ tiếp xúc với đường tròn tại 1 điểm.

+) Nếu $d (O; a) > R \Rightarrow a$ không cắt đường tròn.

Cách giải:

Ta có: $d (O; a) = \sqrt{8}; R = 3 \Rightarrow d (O; a) < R$

Nên đường thẳng $a$ cắt đường tròn $(O; R)$ tại hai điểm phân biệt.

Câu 9:

Rút gọn các biểu thức

A = \frac{1}{2 - \sqrt{3}} + \frac{1}{2 + \sqrt{3}}

Xem đáp án

$A = \frac{1}{2 - \sqrt{3}} + \frac{1}{2 + \sqrt{3}} = \frac{2 + \sqrt{3} + 2 - \sqrt{3}}{(2 - \sqrt{3}) (2 + \sqrt{3})} = \frac{4}{2^{2} - 3} = 4$

Vậy $A = 4.$

Câu 10:

Rút gọn các biểu thức

B = \sqrt{5 + 2 \sqrt{{(1 - \sqrt{2})}^{2}}}

Xem đáp án

$B = \sqrt{5 + 2 \sqrt{{(1 - \sqrt{2})}^{2}}} = \sqrt{5 + 2. (\sqrt{2} - 1)} = \sqrt{5 + 2 \sqrt{2} - 2} = \sqrt{3 + 2 \sqrt{2}} = \sqrt{{(\sqrt{2} + 1)}^{2}} = \sqrt{2} + 1.$

Vậy $B = \sqrt{2} + 1.$

Câu 11:

Rút gọn các biểu thức $C = \frac{x + \sqrt{x} - 2}{\sqrt{x} + 2}$ (với $x \geq 0$ )

Xem đáp án

$C = \frac{x + \sqrt{x} - 2}{\sqrt{x} + 2} (x \geq 0) = \frac{x + 2 \sqrt{x} - \sqrt{x} - 2}{\sqrt{x} + 2} = \frac{(\sqrt{x} + 2) (\sqrt{x} - 1)}{\sqrt{x} + 2} = \sqrt{x} - 1.$

Vậy $C = \sqrt{x} - 1$ với $x \geq 0.$

Câu 12:

Cho hàm số $y = (2 - m) x + 2$ với m là tham số và $m \neq 2,$ có đồ thị là đường thẳng d

Vẽ đồ thị của hàm số trên với m=3

Xem đáp án

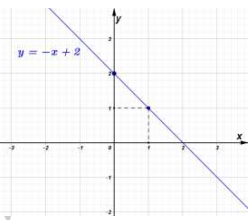
Thay $m = 3$ vào hàm số đã cho ta được: $y = (2 - 3) x + 2 \Rightarrow y = - x + 2$

Ta có bảng giá trị của d:

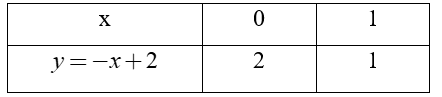
Vậy với $m = 3$ thì đồ thị hàm số là đường thẳng đi qua hai điểm $(0; 2); (1; 1) .$

Câu 13:

Cho hàm số

y = (2 - m) x + 2

với m là tham số và

m \neq 2,

có đồ thị là đường thẳng d

Xác định giá trị của m để đường thẳng y=2x-4 cắt đường thẳng tại một điểm nằm trên trục hoành.

Xem đáp án

Gọi $M (x_{0}; 0)$ là giao điểm của đồ thị đường thẳng $y = 2 x - 4$ và trục Ox

$\Rightarrow 0 = 2 x_{0} - 4 \Leftrightarrow x_{0} = 2 \Rightarrow M (2; 0) .$

Lại có d cắt đường thẳng $y = 2 x - 4$ tại $M (2; 0)$

$\Rightarrow 0 = (2 - m) .2 + 2 \Leftrightarrow 2 - m = - 1 \Leftrightarrow m = 3 (t m) .$

Vậy $m = 3.$

Câu 14:

Cho đường tròn $(O; R),$ đường kính $A B .$ Qua A vẽ đường thẳng d là tiếp tuyến của đường tròn $(O; R) .$ C là một điểm thuộc đường thẳng d. Qua C vẽ tiếp tuyến thứ hai của đường tròn $(O; R) .$ tiếp xúc với đường tròn $(O; R)$ tại điểm M. Gọi H là giao điểm của AM và OC

Chứng minh AM vuông góc với OC và $O H . O C = R^{2} .$

Xem đáp án

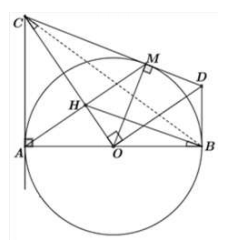
Theo giả thiết ta có hai đường tiếp tuyến tại A và M của đường tròn $(O)$ cặt nhau tại C

$\Rightarrow O C$ là tia phân giác của $∠ A C M$ và $∠ A O M$ (tính chất hai tiếp tuyến cắt nhau).

Xét $Δ A O M$ có: $O A = O M (= R)$ và có $O C$ là tia phân giác của $∠ A O M (c m t)$

$\Rightarrow O C$ đồng thời là đường cao của tam giác cân $A O M .$ (tính chất)

$\Rightarrow O C ⊥ A M = \{H\}$

Vậy $A M ⊥ O C .$

Áp dụng hệ thức lượng cho $Δ O M C$ vuông tại M có đường cao OH có:

$O H . O C = O M^{2} \Leftrightarrow O H . O C = R^{2} . (d p c m)$

Vậy $O H . O C = R^{2}$

Câu 15:

Cho đường tròn

(O; R),

đường kính

A B .

Qua A vẽ đường thẳng d là tiếp tuyến của đường tròn

(O; R) .

C là một điểm thuộc đường thẳng d. Qua C vẽ tiếp tuyến thứ hai của đường tròn

(O; R) .

tiếp xúc với đường tròn

(O; R)

tại điểm M. Gọi H là giao điểm của AM và OC

Chứng minh các góc OBH và OCB bằng nhau.

Xem đáp án

Ta có: $O H . O C = R^{2} = O B^{2}$

$\Rightarrow \frac{O H}{O B} = \frac{O B}{O C}$

Xét $Δ O B H$ và $Δ O C B$ có:

$\frac{O H}{O B} = \frac{O B}{O C}$

góc COB chung

$\Rightarrow Δ O B H ~ Δ O C B (c - g - c) .$

$\Rightarrow ∠ O B H = ∠ O C B$ (hai góc tương ứng bằng nhau). (đpcm)

Vậy $∠ O B H = ∠ O C B .$

Câu 16:

Cho đường tròn

(O; R),

đường kính

A B .

Qua A vẽ đường thẳng d là tiếp tuyến của đường tròn

(O; R) .

C là một điểm thuộc đường thẳng d. Qua C vẽ tiếp tuyến thứ hai của đường tròn

(O; R) .

tiếp xúc với đường tròn

(O; R)

tại điểm M. Gọi H là giao điểm của AM và OC

Qua O vẽ đường thẳng vuông góc với OC, đường thẳng này cắt CM tại D.Chứng minh DB là tiếp tuyến của đường tròn $(O; R) .$

Xem đáp án

Từ giả thiết ta có:

$\{\begin{cases} ∠ D O B + ∠ C O A = 180 ° - ∠ D O C = 180 ° - 90 ° = 90 ° \\ ∠ D O M + ∠ M O C = ∠ D O C = 90 ° \end{cases}$

Mà $∠ M O C = ∠ C O A$ (cm a))

$\Rightarrow ∠ D O B = ∠ D O M$ (cùng phụ với hai hai góc bằng nhau)

Xét $Δ D O B$ và $Δ D O M$ có:

$O D$ chung

$∠ D O B = ∠ D O M (c m t) O B = O M (= R)$

$\Rightarrow Δ D O B = Δ D O M (c - g - c) \Rightarrow ∠ O M D = ∠ O B D = 90 °$

Hay $O B ⊥ B D .$

$\Rightarrow B D$ là tiếp tuyến của đường tròn $(O) .$ (đpcm)

Câu 17:

Cho đường tròn

(O; R),

đường kính

A B .

Qua A vẽ đường thẳng d là tiếp tuyến của đường tròn

(O; R) .

C là một điểm thuộc đường thẳng d. Qua C vẽ tiếp tuyến thứ hai của đường tròn

(O; R) .

tiếp xúc với đường tròn

(O; R)

tại điểm M. Gọi H là giao điểm của AM và OC

Qua O vẽ đường thẳng vuông góc với OC, đường thẳng này cắt CM tại D.Chứng minh DB là tiếp tuyến của đường tròn $(O; R) .$

Xem đáp án

Từ giả thiết ta có:

$\{\begin{cases} ∠ D O B + ∠ C O A = 180 ° - ∠ D O C = 180 ° - 90 ° = 90 ° \\ ∠ D O M + ∠ M O C = ∠ D O C = 90 ° \end{cases}$

Mà $∠ M O C = ∠ C O A$ (cm a))

$\Rightarrow ∠ D O B = ∠ D O M$ (cùng phụ với hai hai góc bằng nhau)

Xét $Δ D O B$ và $Δ D O M$ có:

$O D$ chung

$∠ D O B = ∠ D O M (c m t) O B = O M (= R)$

$\Rightarrow Δ D O B = Δ D O M (c - g - c) \Rightarrow ∠ O M D = ∠ O B D = 90 °$

Hay $O B ⊥ B D .$

$\Rightarrow B D$ là tiếp tuyến của đường tròn $(O) .$ (đpcm)

Câu 18:

Cho x,y thỏa mãn điều kiện: $3 (x \sqrt{y - 9} + y \sqrt{x - 9}) = x y .$ Tính giá trị của biểu thức: $S = {(x - 17)}^{2018} + {(y - 19)}^{2019}$

Xem đáp án

Phương pháp:

Áp dụng bất đẳng thức $a b \leq \frac{a^{2} + b^{2}}{2} \forall a, b$ để chứng minh $V T \geq V P .$

Khi đó dấu “=” xảy ra và ta tìm được x, y.

Cách giải

ĐKXĐ: $\{\begin{cases} x - 9 \geq 0 \\ y - 9 \geq 0 \end{cases} \Rightarrow \{\begin{cases} x \geq 9 \\ y \geq 9 \end{cases}$

Ta có:

$3 (x \sqrt{y - 9} + y \sqrt{x - 9}) = 3 x \sqrt{y - 9} + 3 y \sqrt{x - 9} = 3 \sqrt{x} . \sqrt{x} . \sqrt{y - 9} + 3 \sqrt{y} . \sqrt{y} . \sqrt{x - 9} = 3 \sqrt{x} . \sqrt{x y - 9 x} + 3 \sqrt{y} . \sqrt{x y - 9 y} = \sqrt{9 x} . \sqrt{x y - 9 x} + \sqrt{9 y} . \sqrt{x y - 9 y}$

Với mọi $a, b$ ta có: ${(a - b)}^{2} \geq 0 \Rightarrow a^{2} + b^{2} - 2 a b \geq 0 \Rightarrow 2 a b \leq a^{2} + b^{2} \Rightarrow a b \leq \frac{a^{2} + b^{2}}{2}$

Dấu “=” xảy ra khi và chỉ khi ${(a - b)}^{2} = 0 \Rightarrow a = b$

$\Rightarrow \{\begin{cases} \sqrt{9 x} . \sqrt{x y - 9 x} \leq \frac{9 x + x y - 9 x}{2} = \frac{x y}{2} \\ \sqrt{9 y} . \sqrt{x y - 9 y} \leq \frac{9 y + x y - 9 y}{2} = \frac{x y}{2} \end{cases} \Rightarrow \sqrt{9 x} . \sqrt{x y - 9 x} + \sqrt{9 y} . \sqrt{x y - 9 y} \leq \frac{x y}{2} + \frac{x y}{2} = x y \Rightarrow V T \leq V P$

Mà theo đề bài $V T = V P$ nên dấu “=” xảy ra

$\Rightarrow \{\begin{cases} \sqrt{9 x} = \sqrt{x y - 9 x} \\ \sqrt{9 y} = \sqrt{x y - 9 y} \end{cases} \Rightarrow \{\begin{cases} 9 x = x y - 9 x \\ 9 y = x y - 9 y \end{cases} \Rightarrow \{\begin{cases} x (y - 18) = 0 \\ y (x - 18) = 0 \end{cases} \Rightarrow x = y = 18 (d o x \geq 9, y \geq 9) \Rightarrow S = {(x - 17)}^{2018} + {(y - 19)}^{2019} = {(18 - 17)}^{2018} + {(18 - 19)}^{2019} = 1 - 1 = 0.$

Vậy $S = 0.$