Bộ 15 đề kiểm tra học kì 1 Toán 9 năm 2022-2023 có đáp án (Đề 12)
-
2214 lượt thi
-
12 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
Rút gọn căn bậc hai bằng công thức: .
Câu 2:
 Xem đáp án
Xem đáp án
Quy đồng mẫu số và rút gọn biểu thức.
Câu 6:
Tính giá trị biểu thức C khi .
 Xem đáp án
Xem đáp án
Điều kiện: .
Có: (tmđk)
Thay vào ta được: .
Vậy khi thì .
Câu 7:
Tìm các giá trị của a sao cho C<0.
 Xem đáp án
Xem đáp án
Điều kiện xác định: .
(do )
Kết hợp điều kiện xác định .
Vậy thì .
Câu 8:
Cho hai đường thẳng và .
Tìm điều kiện của m để hàm số có đồ thị luôn nghịch biến và điều kiện của n để hàm số có đồ thị luôn đồng biến.
 Xem đáp án
Xem đáp án
Hàm số có đồ thị luôn nghịch biến .
Hàm số có đồ thị luôn đồng biến .
Vậy thì hàm số có đồ thị luôn nghịch biến.
thì hàm số có đồ thị luôn đồng biến.
Câu 9:
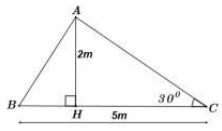
Để lợp một mái nhà bằng tôn, thợ sắt hàn khung sắt hình tam giác ABC (xem hình vẽ), biết một kích thước của khung sắt là , chiều cao khung sắt là và độ dốc mái tôn phía sau là . Tìm độ dài AB của khung sắt phía trước.
(Kết quả cuối cùng làm tròn đến 2 chữ số thập phân).
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng công thức tính tan 1 góc để tính cạnh AH và định lý Pytago trong vuông tại H để tính cạnh AB.
Cách giải:
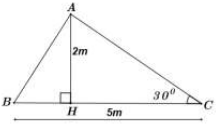
Xét vuông tại H ta có:
Xét vuông tại H, theo định lý Pytago ta có:
Vậy .
Câu 10:
Cho đường tròn tâm O đường kính BC, lấy điểm A bất kỳ trên đường tròn (O) (A khác B và C). Kẻ tại E và kẻ tại F, tiếp tuyến tại B của đường tròn cắt CA tại D. Tia OE cắt BD tại M. Gọi I là giao điểm của BF và AO, gọi K là giao điểm của IC và OF.
Chứng minh tứ giác OEAF là hình chữ nhật và .
 Xem đáp án
Xem đáp án
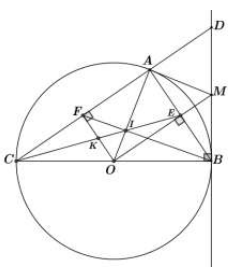
Xét có:
và O là trung điểm của BC (gt)
vuông tại A.
Xét tứ giác OEAF ta có:
là hình chữ nhật. (dhnb).
Ta có BD là tiếp tuyến của đường tròn (O)
hay
Xét vuông tại B có (do ), theo hệ thức lượng tròn tam giác vuông, ta có:
(đpcm).
Câu 11:
Chứng minh MA là tiếp tuyến của đường tròn (O).
 Xem đáp án
Xem đáp án
Xét có: .
là đường cao đồng thời là đường phân giác của cân tại O.(tính chất).
hay .
Xét và ta có:
(cmt)
OM chung.
(c.g.c)
MA là tiếp tuyến của đường tròn (O). (đpcm)
Câu 12:
Chứng minh K là trung điểm của OF.
 Xem đáp án
Xem đáp án
Ta dễ dàng chứng minh được E, F là trung điểm của AB và AC (do và cân tại O)
Xét có hai đường trung tuyến BF và AO cắt nhau tại I (gt)
I là trọng tâm của .
C, K, I, E thẳng hàng.
Ta có: OF là đường trung tuyến của .
(1)
Mặt khác trong có:
O là trung điểm của BC
(do )
chính là đường trung bình của (định lý đảo).
K là trung điểm của OF. (đpcm).
