23 câu hỏi trắc nghiệm thuộc Bộ 15 đề kiểm tra học kì 1 Toán 9 năm 2022-2023 có đáp án (Đề 11)

Câu 1:

x < 0

hãy rút gọn biểu thức :

N = \sqrt{x^{2}} + \sqrt[3]{x^{3}}

A. $N = 2 x .$

B.

N = 0.

C.

N = x .

D. $N = - 2 x .$

Xem đáp án

Đáp án B

Phương pháp

Áp dụng công thức $\sqrt{A^{2}} = [\begin{array}{l} A k h i A \geq 0 \\ - A k h i A < 0 \end{array}$ .

Cách giải

Với $x < 0$ thì $N = \sqrt{x^{2}} + \sqrt[3]{x^{3}} = |x| + x = - x + x = 0$ .

Câu 2:

Cho đường tròn (O, 6cm), khoảng cách từ tâm O đến dây cung bằng 4cm. Độ dài dây cung là:

A. $4 \sqrt{2} c m$ .

B.

2 \sqrt{13} c m

.

C.

4 \sqrt{5} c m

.

D.

2 \sqrt{5} c m

.

Xem đáp án

Đáp án C

Phương pháp

Định lý: Đường kính vuông góc với dây cung thì đi qua trung điểm của dây ấy.

Áp dụng công thức tính độ dài dây cung: $l = 2 \sqrt{R^{2} - d^{2}}$ (với d là khoảng cách từ tâm đến dây cung).

Cách giải

Áp dụng công thức ta có độ dài dây cung là:

$l = 2 \sqrt{R^{2} - d^{2}} = 2 \sqrt{6^{2} - 4^{2}} = 2 \sqrt{36 - 16} = 2 \sqrt{20} = 2.2 \sqrt{5} = 4 \sqrt{5} (c m)$ .

Câu 3:

Với $x \neq 0$ và $y < 0$ . Tính giá trị của biểu thức $M = \frac{3}{2 x^{2} y} . \sqrt{4 x^{4} y^{2}}$ .

A. $M = 3.$

B.

M = 6.

C.

M = - 3.

D.

M = - 6.

Xem đáp án

Đáp án C

Phương pháp

Áp dụng công thức $\sqrt{A^{2}} = [\begin{array}{l} A k h i A \geq 0 \\ - A k h i A < 0 \end{array}$ .

Cách giải

Với $x \neq 0; y < 0$ thì $M = \frac{3}{2 x^{2} y} . \sqrt{4 x^{4} y^{2}} = \frac{3}{2 x^{2} y} . |2 x^{2} y| = \frac{3}{2 x^{2} y} .2 x^{2} . (- y) = - 3$ .

Câu 4:

Tìm x biết $5 \sqrt{x} = 10$ .

A. $x = 4.$

B.

x = \pm 4.

C.

x = 2.

D.

x = \pm 2.

Xem đáp án

Đáp án A

Phương pháp

Áp dụng quy tắc: $\sqrt{A} = B (B \geq 0) \Leftrightarrow A = B^{2}$ .

Cách giải

Điều kiện: $x \geq 0$ .

$5 \sqrt{x} = 10 \Leftrightarrow \sqrt{x} = 2 \Leftrightarrow x = 4 (t m)$

Câu 5:

Điều kiện của x để biểu thức $\sqrt{3 - x}$ có nghĩa là:

A. $x \leq 3.$

B.

x > 3.

C.

x < 3.

D. $x \geq 3.$

Xem đáp án

Đáp án A

Phương pháp

Điều kiện để $\sqrt{A}$ có nghĩa là $A \geq 0$ .

Cách giải

$\sqrt{3 - x}$ có nghĩa $\Leftrightarrow 3 - x \geq 0 \Leftrightarrow x \leq 3$ .

Câu 6:

Trong các hàm số sau, đồ thị hàm số nào là đường thẳng tạo với trục hoành một góc

45 °

.

A. $y = 45 x - 1$ .

B.

y = - 45 x - 1

.

C.

y = x - 45

.

D.

y = 2 x + 45

.

Xem đáp án

Đáp án C

Phương pháp

Gọi $α$ là góc tạo bởi đường thẳng $y = a x + b (a \neq 0)$ với trục hoành.

Ta có: $\tan α = a \Rightarrow α$ là góc nhọn nếu $a > 0, α$ là góc tù nếu $a < 0$ .

Cách giải

Đường thẳng tạo với trục hoành góc $45 ° \Rightarrow \tan α = 1$ .

Câu 7:

Nếu đường thẳng y=kx-2 đi qua điểm A(-1,5) thì hệ số góc của nó bằng mấy?

A. 10.

B.

- 3.

C. 7.

D. -7

Xem đáp án

Đáp án D

Phương pháp

Thay tọa độ điểm A vào phương trình đường thẳng để tìm hệ số k.

Cách giải

Thay tọa độ điểm $A (- 1; 5)$ vào phương trình $y = k x - 2$ ta được: $5 = k . (- 1) - 2 \Rightarrow k = - 7$ .

Câu 8:

Tìm m để hàm số y=(1-2m)x+3 là hàm số đồng biến?

A. $m < \frac{1}{2} .$

B.

m > \frac{1}{2} .

C.

m \leq \frac{1}{2} .

D. $m \geq \frac{1}{2} .$

Xem đáp án

Đáp án A

Phương pháp

Hàm số $y = a x + b (a \neq 0)$ đồng biến $\Leftrightarrow a > 0$ , nghịch biến $\Leftrightarrow a < 0$ .

Cách giải

Hàm số $y = (1 - 2 m) x + 3$ đồng biến $\Leftrightarrow 1 - 2 m > 0 \Rightarrow m < \frac{1}{2}$ .

Câu 9:

Một tam giác vuông có một cạnh góc vuông gấp đôi cạnh góc vuông còn lại. Hỏi cạnh huyền gấp bao nhiêu lần cạnh góc vuông nhỏ nhất?

A. 5.

B. 3

C.

\sqrt{5}

D. $\sqrt{3}$

Xem đáp án

Đáp án C

Phương pháp

Áp dụng định lý Pytago trong tam giác vuông.

Cách giải

Gọi cạnh góc vuông nhỏ của tam giác vuông bài cho là $a (a > 0)$ .

Khi đó cạnh góc vuông còn lại là: 2a.

Áp dụng định lý Pytago ta có cạnh huyền là: $\sqrt{a^{2} + {(2 a)}^{2}} = \sqrt{5 a^{2}} = a \sqrt{5}$ .

Cạnh huyền gấp $\sqrt{5}$ lần cạnh góc vuông nhỏ nhất của tam giác đó.

Câu 10:

Cho hai đường tròn (O; 4cm) và (I, 6cm). Biết OI=2cm. Tìm vị trí tương đối của hai đường tròn.

A. Tiếp xúc ngoài.

B. Đựng nhau.

C. Tiếp xúc trong.

D. Cắt nhau.

Xem đáp án

Đáp án C

Phương pháp

Vị trí tương đối của hai đường tròn $(O_{1}; R_{1})$ và $(O_{2}; R_{2}), O_{1} O_{2} = d$ là:

+ Cắt nhau tại 2 điểm khi $R_{1} + R_{2} > d > 0$

+ Đựng nhau khi: $|R_{1} - R_{2}| > d$ .

+ Tiếp xúc ngoài khi: $R_{1} + R_{2} = d$ .

+ Tiếp xúc trong khi: $|R_{1} - R_{2}| = d$ .

Cách giải

Ta có: $R_{1} = 6 c m; R_{2} = 4 c m; d = 2 c m \Rightarrow R_{1} - R_{2} = d = 2 c m$ .

$\Rightarrow$ Hai đường tròn tiếp xúc trong.

Câu 11:

Cho tam giác ABC vuông tại A, đường cao AH. Hệ thức nào dưới đây SAI?

A. $A B . A C = B C . A H$ .

B.

\frac{1}{B C^{2}} = \frac{1}{A B^{2}} + \frac{1}{A C^{2}}

.

C.

A B^{2} = B H . B C

.

D.

A H^{2} = H B . H C

.

Xem đáp án

Đáp án B

Phương pháp

Áp dụng các hệ thức lượng trong tam giác.

Cách giải

Ý A: đúng.

Ý B: sai. Công thức đúng là theo định lý Pytago: $B C^{2} = A B^{2} + A C^{2}$ .

Ý C: đúng.

Ý D: đúng.

Câu 12:

Phương trình đường thẳng d có hệ số góc bằng 5 và đi qua điểm A(-1;1) là:

A. $y = 5 x - 6.$

B.

y = 5 x + 6.

C.

y = 5 x + 4.

D.

y = 5 x - 4.

Xem đáp án

Đáp án B

Phương pháp

Gọi phương trình đường thẳng cần tìm theo công thức chung và theo những dữ kiện đã cho của bài để giải.

Cách giải

Gọi phương trình đường thẳng cần tìm có dạng: $y = a x + b$ .

Theo bài ta có: $a = 5$ và đi qua điểm $A (- 1; 1)$ nên $1 = 5. (- 1) + b \Rightarrow b = 6$ .

Vậy phương trình cần tìm là $y = 5 x + 6$ .

Câu 13:

Khẳng định nào dưới đây là đúng?

A. $\sin α = \cos (90 ° - α) .$

B.

\sin α^{2} + \cos α^{2} = 1.

C.

\tan α = \tan (90 ° - α) .

D.

\cot α = \cot (90 ° - α) .

Xem đáp án

Đáp án A

Phương pháp

Áp dụng các công thức lượng giác cơ bản.

Cách giải

+ Đáp án A: đúng.

+ Đáp án B: sai, công thức đúng: $\sin^{2} α + \cos^{2} α = 1$ .

+ Đáp án C: sai, công thức đúng: $\tan α = \cot (90 ° - α)$ .

+ Đáp án D: sai, công thức đúng: $\cot α = \tan (90 ° - α)$ .

Câu 14:

Điểm $A (\frac{1}{2}; 1)$ thuộc đồ thị hàm số nào trong các hàm số dưới đây?

A. $y = 2 x - 1.$

B.

y = - 2 x + 2.

C.

y = 2 x + 1.

D.

y = - 2 x + 1.

Xem đáp án

Đáp án B

Phương pháp

Thay tọa độ điểm A vào lần lượt các đáp án.

Cách giải

Thay tọa độ điểm $A (\frac{1}{2}; 1)$ vào phương trình các đường thẳng ta được:

+ Ý A: $1 = 2. \frac{1}{2} - 1 \Leftrightarrow 1 = 0$ (loại).

+ Ý B: $1 = - 2. \frac{1}{2} + 2 \Rightarrow 1 = 1$ (đúng) chọn đáp án B.

Câu 15:

Tìm khẳng định đúng trong các khẳng định sau:

A. $\sqrt{\frac{6}{{(- 5)}^{2}}} = \frac{\sqrt{6}}{- 5}$ .

B.

\sqrt{\frac{2}{a^{2}}} = \frac{\sqrt{2}}{a}

, với

a \neq 0

.

C.

\sqrt{\frac{6}{5^{2}}} = \frac{\sqrt{6}}{5}

.

D.

\sqrt{\frac{16}{a^{2}}} = \frac{4}{a}

, với

a \neq 0

.

Xem đáp án

Đáp án C

Phương pháp

Áp dụng công thức: $\sqrt{A^{2}} = [\begin{array}{l} A k h i A \geq 0 \\ - A k h i A < 0 \end{array}$ .

Cách giải

+ Đáp án A: $\sqrt{\frac{6}{{(- 5)}^{2}}} = \frac{\sqrt{6}}{- 5} = \frac{\sqrt{6}}{5} \Rightarrow$ A sai.

+ Đáp án B: $\sqrt{\frac{2}{a}} = \frac{\sqrt{2}}{|a|} = [\begin{array}{l} \frac{\sqrt{2}}{a} k h i a > 0 \\ \frac{\sqrt{2}}{- a} k h i a < 0 \end{array} \Rightarrow$ B sai.

+ Đáp án C: Đúng.

+ Đáp án D: $\sqrt{\frac{16}{a^{2}}} = \frac{4}{|a|} = [\begin{array}{l} \frac{4}{a} k h i a > 0 \\ \frac{4}{- a} k h i a < 0 \end{array} \Rightarrow$ D sai.

Câu 16:

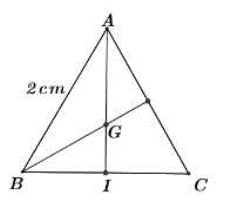
Cho tam giác đều ABC cạnh bằng 2cm. Tính bán kính R của đường tròn ngoại tiếp tam giác ABC.

A. $R = 3 c m .$

B.

R = \frac{2 \sqrt{5}}{5} c m .

C.

R = \frac{2 \sqrt{3}}{3} c m .

D.

R = \sqrt{3} c m .

Xem đáp án

Đáp án C

Phương pháp

Tam giác đều thì tâm đường tròn ngoại tiếp tam giác trùng với trọng tâm, từ đó áp dụng định lý Pytago.

Cách giải

Gọi I là trung điểm của BC, G là trọng tâm tam giác ABC và R là bán kính đường tròn ngoại tiếp tam giác ABC thì $R = A G = \frac{2}{3} . A I$ .

Trong tam giác ABI vuông tại I có:

$A I^{2} = A B^{2} - I B^{2} = 2^{2} - 1 = 3 \Rightarrow A I = \sqrt{3} (c m)$

Khi đó: $R = \frac{2}{3} . A I = \frac{2 \sqrt{3}}{3} c m$ .

Câu 17:

Tìm x biết $\sqrt{2} x - \sqrt{50} = 0$ .

Xem đáp án

ĐKXĐ: $x \geq 0$ .

$\sqrt{2 x} - \sqrt{50} = 0 \Leftrightarrow \sqrt{2 x} = \sqrt{50} \Leftrightarrow 2 x = 50 \Leftrightarrow x = 25 (t m d k)$

Vậy $x = 25$ .

Câu 18:

Tìm giá trị của biểu thức

A = \frac{1}{\sqrt{3} - 2} - \frac{1}{\sqrt{3} + 2}

.

Xem đáp án

$A = \frac{1}{\sqrt{3} - 2} - \frac{1}{\sqrt{3} + 2} = \frac{(\sqrt{3} + 2) - (\sqrt{3} - 2)}{(\sqrt{3} + 2) (\sqrt{3} - 2)} = \frac{\sqrt{3} + 2 - \sqrt{3} + 2}{{(\sqrt{3})}^{2} - 2^{2}} = \frac{4}{3 - 4} = - 4$

Vậy $A = - 4$ .

Câu 19:

Trên mặt phẳng tọa độ Oxy cho hai điểm A, B như hình bên.

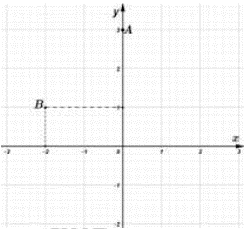
Media VietJack

Hãy xác định tọa độ của hai điểm A, B.

Xem đáp án

Dựa vào đồ thị hàm số ta xác định được: $A (0; 3)$ và $B (- 2; 1)$ .

Câu 20:

Trên mặt phẳng tọa độ Oxy cho hai điểm A, B như hình bên.

Viết phương trình đường thẳng d đi qua hai điểm A, B.

Xem đáp án

Gọi phương trình đường thẳng $(d)$ đi qua hai điểm A và B có dạng: $y = a x + b$ .

Do $A \in (d); B \in (d)$ nên thay tọa độ hai điểm vào phương trình, ta được:

$\{\begin{cases} 3 = a .0 + b \\ 1 = a . (- 2) + b \end{cases} \Rightarrow \{\begin{cases} b = 3 \\ - 2 a = 1 - b \end{cases} \Rightarrow \{\begin{cases} b = 3 \\ - 2 a = 1 - 3 = - 2 \end{cases} \Rightarrow \{\begin{cases} b = 3 \\ a = 1 \end{cases} \Rightarrow (d) : y = x + 3$

Vậy: $(d) : y = x + 3$ .

Câu 21:

Cho đường tròn tâm O bán kính 13cm và dây $A B = 24 c m$ của đường tròn. Gọi I là trung điểm của AB. Từ A và B vẽ hai tiếp tuyến với đường tròn, chúng cắt nhau tại C.

Vẽ hình và tính độ dài của OI.

Xem đáp án

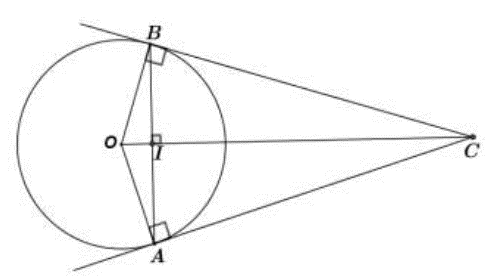
Do $A B < 2 R$ nên AB không đi qua O.

Xét $Δ O A B$ có: $O A = O B = R$ và I là trung điểm của AB.

$\Rightarrow$ OI là đường trung tuyến đồng thời là đường cao của $Δ O A B$ cân tại O (tính chất).

$\Rightarrow O I ⊥ A B = \{I\}$

Áp dụng định lý Pytago trong $Δ O I B$ vuông tại I có: $O I^{2} + I B^{2} = O B^{2}$ .

$\Rightarrow O I^{2} = O B^{2} - I B^{2} = 13^{2} - {(\frac{24}{2})}^{2} = 25 \Rightarrow O I = 5 (c m)$

Vậy: $O I = 5 c m$ .

Câu 22:

Cho đường tròn tâm O bán kính 13cm và dây

A B = 24 c m

của đường tròn. Gọi I là trung điểm của AB. Từ A và B vẽ hai tiếp tuyến với đường tròn, chúng cắt nhau tại C.

Chứng minh rằng OC đi qua điểm I và tính độ dài OC.

Xem đáp án

Ta có: CB và CA là hai tiếp tuyến của $(O)$ cắt nhau tại C.

$\Rightarrow A C = C B \Rightarrow C$ thuộc đường trung trực của AB.

Lại có: $O A = O B = R \Rightarrow O$ thuộc đường trung trực của AB.

Mà I là trung điểm của AB.

$\Rightarrow I \in O C$ (đpcm).

Áp dụng hệ thức lượng trong $Δ O B C$ vuông tại B có đường cao BI ta có:

$O B^{2} = O I . O C \Rightarrow O C = \frac{O B^{2}}{O I} = \frac{13^{2}}{5} = \frac{169}{5} = 33, 8 (c m)$

Vậy: $O C = 33, 8 c m$ .

Câu 23:

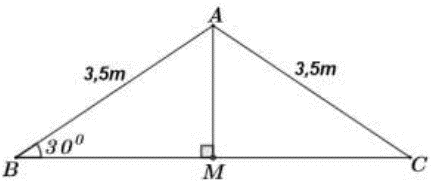
Bạn An đang học vẽ hình bằng phần mềm máy tính. An vẽ hình một ngôi nhà với phần mái có dạng hình tam giác cân (hình vẽ bên). Biết góc tạo bởi phần mái và mặt phẳng nằm ngang là $30 °$ , chiều dài mỗi bên dốc mái là 3,5m. Tính gần đúng bề rộng của mái nhà.

Xem đáp án

Phương pháp

Áp dụng phương pháp tính cạnh trong tam giác vuông khi biết 1 góc và cạnh huyền.

Cách giải

Ta vẽ lại mô hình mái nhà như hình vẽ bên.

Theo đề bài cho ta có: $Δ A B C$ cân tại A.

$A B = A C = 3, 5 m$ và $∠ B = ∠ C = 30 °$ .

Thì khi đó bề rộng mái nhà chính là độ dài cạnh BC.

Gọi M là trung điểm của BC.

$\Rightarrow$ AM là đường trung tuyến đồng thời là đường cao của (tính chất).

Xét $Δ A B M$ vuông tại M ta có:

$\begin{array}{l} \cos B = \frac{B M}{A B} \Rightarrow \cos 30 ° = \frac{B M}{3, 5} \Rightarrow B M = \cos 30 ° .3, 5 = \frac{\sqrt{3}}{2} .3, 5 = \frac{7 \sqrt{3}}{4} (m) \\ \Rightarrow B C = 2 B M = \frac{7 \sqrt{3}}{2} (m) \approx 6, 06 m \end{array}$

Vậy bề rộng mái nhà là 6,06m.