13 câu hỏi trắc nghiệm thuộc Bộ 15 đề kiểm tra học kì 1 Toán 9 năm 2022-2023 có đáp án (Đề 5)

Câu 1:

Rút gọn các biểu thức $A = 3 \sqrt{\frac{1}{3}} + \frac{1}{2} \sqrt{48} + \sqrt{75}$

Đưa thừa số ra ngoài dấu căn $\sqrt{A^{2} B} = |A| . \sqrt{B} .$

Ta có:

$A = 3 \sqrt{\frac{1}{3}} + \frac{1}{2} \sqrt{48} + \sqrt{75} = 3. \frac{\sqrt{3}}{3} + \frac{1}{2} .4 \sqrt{3} + 5 \sqrt{3} = \sqrt{3} + 2 \sqrt{3} + 5 \sqrt{3} = 8 \sqrt{3}$

Câu 2:

Rút gọn các biểu thức

B = 3 \sqrt{20} - 20 \sqrt{\frac{1}{5}} - \frac{4}{\sqrt{5} + \sqrt{3}}

Xem đáp án

Đưa thừa số ra ngoài dấu căn $\sqrt{A^{2} B} = |A| . \sqrt{B} .$

Trục căn thức ở mẫu $\frac{C}{\sqrt{A} + \sqrt{B}} = \frac{C (\sqrt{A} - \sqrt{B})}{A - B} .$

Ta có:

$B = 3 \sqrt{20} - 20 \sqrt{\frac{1}{5}} - \frac{4}{\sqrt{5} + \sqrt{3}} = 3.2 \sqrt{5} - 20. \frac{\sqrt{5}}{5} - \frac{4 (\sqrt{5} - \sqrt{3})}{(\sqrt{5} + \sqrt{3}) (\sqrt{5} - \sqrt{3})} B = 6 \sqrt{5} - 4 \sqrt{5} - \frac{4 (\sqrt{5} - \sqrt{3})}{5 - 3} = 2 \sqrt{5} - 2 \sqrt{5} + 2 \sqrt{3} = 2 \sqrt{3} .$

Câu 3:

Cho hai biểu thức $A = \frac{2 \sqrt{x} - 4}{\sqrt{x} - 1}$ và $B = \frac{\sqrt{x}}{\sqrt{x} - 1} + \frac{3}{\sqrt{x} + 1} + \frac{6 \sqrt{x} - 4}{1 - x} (x \geq 0; x \neq 1) .$

Tính giá trị của biểu thức A khi x=9.

Xem đáp án

Điều kiện: $x \geq 0, x \neq 1$ .

Thay $x = 9$ (tmđk) vào biểu thức A, ta có: $A = \frac{2 \sqrt{9} - 4}{\sqrt{9} - 1} = \frac{2.3 - 4}{3 - 1} = \frac{2}{2} = 1$ .

Vậy với $x = 9$ thì $A = 1$ .

Câu 4:

Cho hai biểu thức

A = \frac{2 \sqrt{x} - 4}{\sqrt{x} - 1}

và

B = \frac{\sqrt{x}}{\sqrt{x} - 1} + \frac{3}{\sqrt{x} + 1} + \frac{6 \sqrt{x} - 4}{1 - x} (x \geq 0; x \neq 1) .

Rút gọn B .

Xem đáp án

Điều kiện: $x \geq 0, x \neq 1$ .

$B = \frac{\sqrt{x}}{\sqrt{x} - 1} + \frac{3}{\sqrt{x} + 1} + \frac{6 \sqrt{x} - 4}{1 - x} = \frac{\sqrt{x}}{\sqrt{x} - 1} + \frac{3}{\sqrt{x} + 1} - \frac{6 \sqrt{x} - 4}{(\sqrt{x} - 1) (\sqrt{x} + 1)} = \frac{\sqrt{x} (\sqrt{x} + 1) + 3 (\sqrt{x} - 1) - 6 \sqrt{x} + 4}{(\sqrt{x} - 1) (\sqrt{x} + 1)} = = \frac{x + \sqrt{x} + 3 \sqrt{x} - 3 - 6 \sqrt{x} + 4}{(\sqrt{x} - 1) (\sqrt{x} + 1)} = \frac{x - 2 \sqrt{x} + 1}{(\sqrt{x} - 1) (\sqrt{x} + 1)} = \frac{{(\sqrt{x} - 1)}^{2}}{(\sqrt{x} - 1) (\sqrt{x} + 1)} = \frac{\sqrt{x} - 1}{\sqrt{x} + 1}$

Vậy $B = \frac{\sqrt{x} - 1}{\sqrt{x} + 1}$ với $x \geq 0, x \neq 1$ .

Câu 5:

Cho hai biểu thức

A = \frac{2 \sqrt{x} - 4}{\sqrt{x} - 1}

và

B = \frac{\sqrt{x}}{\sqrt{x} - 1} + \frac{3}{\sqrt{x} + 1} + \frac{6 \sqrt{x} - 4}{1 - x} (x \geq 0; x \neq 1) .

Đặt P=A.B. So sánh giá trị của P với 2.

Xem đáp án

Điều kiện: $x \geq 0, x \neq 1$ .

Có $P = A . B = \frac{2 \sqrt{x} - 4}{\sqrt{x} - 1} . \frac{\sqrt{x} - 1}{\sqrt{x} + 1} = \frac{2 \sqrt{x} - 4}{\sqrt{x} + 1}$

Xét $P - 2 = \frac{2 \sqrt{x} - 4}{\sqrt{x} + 1} - 2 = \frac{2 \sqrt{x} - 4 - 2 \sqrt{x} - 2}{\sqrt{x} + 1} = \frac{- 6}{\sqrt{x} + 1}$

Vì $- 6 < 0; \sqrt{x} + 1 \geq 0$ với mọi $x \geq 0, x \neq 1$

$\Rightarrow \frac{- 6}{\sqrt{x} + 1} < 0 \Rightarrow P - 2 < 0 \Rightarrow P < 2$

Vậy $P < 2$

Câu 6:

Cho hàm số $y = (m - 1) x - 4$ có đồ thị là đường thẳng (d).

Tìm m để đường thẳng (d) song song vớ đường thẳng y=2x+5.

Xem đáp án

Đường thẳng (d) song song với đường thẳng $y = 2 x + 5$

$\Leftrightarrow \{\begin{cases} a = a^{'} \\ b \neq b^{'} \end{cases} \Leftrightarrow \{\begin{cases} m - 1 = 2 \\ - 4 \neq 5 \end{cases} \Leftrightarrow m = 3.$

Vậy $m = 3$ thì thỏa mãn bài toán.

Câu 7:

Cho hàm số

y = (m - 1) x - 4

có đồ thị là đường thẳng (d).

Vẽ đồ thị hàm số trên với m tìm được ở câu a.

Xem đáp án

Với $m = 3$ , ta có: $(d) : y = 2 x - 4$ .

Cho $x = 0$ ta được $y = 2.0 - 4 = - 4$ nên $M (0; - 4)$

Cho $y = 0 \Rightarrow 0 = 2 x - 4 \Leftrightarrow x = 2$ nên $N (2; 0)$

Đồ thị hàm số là đường thẳng $(d)$ đi qua hai điểm $(0; - 4)$ và $(2; 0)$

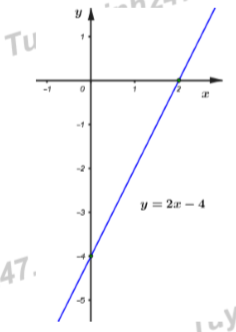
Câu 8:

Cho hàm số

y = (m - 1) x - 4

có đồ thị là đường thẳng (d).

Đường thẳng (d) cắt trục Ox tại A, cắt trục Oy tại B. Tìm m để tam giác OAB vuông cân.

Xem đáp án

$(d)$ cắt hai trục $O x; O y$ tại $A, B$ thì $m - 1 \neq 0 \Leftrightarrow m \neq 1.$

Cho $x = 0 \Rightarrow y = - 4 \Rightarrow B (0; - 4) \Rightarrow O B = |- 4| = 4$ .

Cho $y = 0 \Rightarrow x = \frac{4}{m - 1} \Rightarrow A (\frac{4}{m - 1}; 0) \Rightarrow O A = \frac{4}{|m - 1|}$

Để $Δ O A B$ vuông cân tại $O \Rightarrow O A = O B$

$\Leftrightarrow \frac{4}{|m - 1|} = 4 \Leftrightarrow |m - 1| = 1 \Leftrightarrow [\begin{array}{l} m = 0 \\ m = 2 \end{array} (t m)$

Vậy $m \in \{0; 2\} .$

Câu 9:

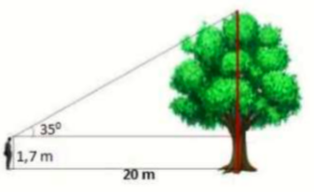
Tính chiều cao của cây trong hình vẽ bên (Làm tròn đến chữ số thập phân thứ nhất)

Xem đáp án

Phương pháp

Sử dụng giá trị lượng giác của một góc nhọn trong tam giác vuông để giải tam giác.

Cách giải

Tính chiều cao của cây trong hình vẽ bên (Làm tròn đến chữ số thập phân thứ nhất)

Chiều cao của cây là: $h = 1, 7 + 20. \tan 35^{°} \approx 15, 7 m .$

Câu 10:

Cho đường tròn $(O)$ và một điểm M nằm ngoài đường tròn. Từ M kẻ hai tiếp tuyến MA, MB với đường tròn $(O)$ (A và B là hai tiếp điểm). Gọi I là giao điểm của OM và AB. Kẻ đường kính BC của $(O)$ .

Chứng minh 4 điểm M,O,A,B cùng thuộc một đường tròn.

Xem đáp án

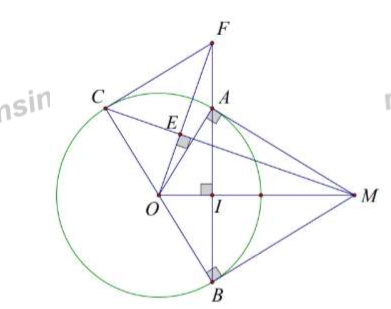
Gọi K là trung điểm $O M \Rightarrow O K = K M$ .

Tam giác OMA vuông tại A nên $A K = K M = K O = \frac{1}{2} O M$ (tính chất trung tuyến tam giác vuông).

Tam giác OBM vuông tại B nên $B K = K M = K O = \frac{1}{2} O M$ (tính chất trung tuyến tam giác vuông).

Do đó $O K = K M = K A = K B$ .

Suy ra 4 điểm $O, A, M, B$ nằm trên đường tròn tâm K, đường kính OM.

Câu 11:

Cho đường tròn

(O)

và một điểm M nằm ngoài đường tròn. Từ M kẻ hai tiếp tuyến MA, MB với đường tròn

(O)

(A và B là hai tiếp điểm). Gọi I là giao điểm của OM và AB. Kẻ đường kính BC của

(O)

.

Chứng minh

O I . O M = O A^{2}

.

Xem đáp án

Ta có: $O A = O B$ (bán kính)

$M A = M B$ (tính chất hai tiếp tuyến cắt nhau)

$\Rightarrow O M$ là trung trực của $A B \Rightarrow O M ⊥ A B$ tại I.

$Δ O A M$ vuông tại A đường cao $A I \Rightarrow O I . O M = O A^{2}$ (hệ thức giữa cạnh và đường cao).

Câu 12:

Cho đường tròn

(O)

và một điểm M nằm ngoài đường tròn. Từ M kẻ hai tiếp tuyến MA, MB với đường tròn

(O)

(A và B là hai tiếp điểm). Gọi I là giao điểm của OM và AB. Kẻ đường kính BC của

(O)

.

Qua (O) vẽ đường thẳng vuông góc với MC tại E cắt đường thẳng BA tại F.

Xem đáp án

Xét $Δ O F I$ và $Δ O M E$ có:

$∠ O$ chung

$∠ O I F = ∠ O E M = 90^{°}$

$\Rightarrow Δ O F I ~ Δ OME (g - g) \Rightarrow \frac{O F}{O M} = \frac{O I}{O E}$ (các cặp cạnh tương ứng tỉ lệ)

$\Rightarrow O F . O E = O I . O M = O A^{2} = O C^{2} \Rightarrow \frac{O F}{O C} = \frac{O C}{O E}$

Xét $Δ O C E$ và $Δ O F C$ có:

$∠ O$ chung

$\frac{O F}{O C} = \frac{O C}{O E} (c m t) \Rightarrow Δ O C E ~ Δ O F C (c - g - c)$

Nên $∠ O C F = ∠ O E C = 90^{°}$ (góc tương ứng)

$\Rightarrow F C$ là tiếp tuyến của $(O)$ (đpcm).

Câu 13:

Cho ba số dương x, y, z thay đổi nhưng luôn thỏa mãn điều kiện $x + y + z = 1$ . Tìm giá trị lớn nhất của biểu thức: $P = \frac{x}{x + 1} + \frac{y}{y + 1} + \frac{z}{z + 1} .$

Xem đáp án

Phương pháp

Nhận xét: $P = 3 - (\frac{1}{x + 1} + \frac{1}{y + 1} + \frac{1}{z + 1})$

Sử dụng bất đẳng thức $\frac{1}{a} + \frac{1}{b} + \frac{1}{c} \geq \frac{9}{a + b + c}$ để đánh giá.

Cách giải:

Ta có: $P = 3 - (\frac{1}{x + 1} + \frac{1}{y + 1} + \frac{1}{z + 1})$

Mà $\frac{1}{x + 1} + \frac{1}{y + 1} + \frac{1}{z + 1} \geq \frac{9}{x + y + z + 3} = \frac{9}{4}$

$\Rightarrow P \leq 3 - \frac{9}{4} = \frac{3}{4}$

Dấu $" = "$ xảy ra khi $x = y = z = \frac{1}{3}$ .

Vậy $\max P = \frac{3}{4} \Leftrightarrow x = y = z = \frac{1}{3} .$