41 câu hỏi trắc nghiệm thuộc Chủ đề 17: Đề kiểm tra có đáp án

Câu 1:

Hai bến sông cách nhau 15km. Thời gian một ca nô xuôi dòng từ bến A đến bến B, tại bến B nghỉ 20 phút rồi ngược dòng từ bến B trở về bến A tổng cộng là 3 giờ. Tính vận tốc của ca nô khi nước yên lặng, biết vận tốc của dòng nước là 3 km/h

Xem đáp án

Đổi 20 phút $\frac{1}{3}$ giờ.

Gọi vận tốc của ca nô khi nước yên lặng là x (km/h) (Điều kiện x > 3).

Vận tốc ca nô lúc xuôi dòng là: x + 3 (km/h).

Vận tốc ca nô lúc ngược dòng là: x - 3 (km/h).

Thời gian ca nô ngược dòng từ A đến B là: 15 : ( x - 3) = $\frac{15}{x - 3}$ (h).

Vì thời gian ca nô xuôi dòng, ngược dòng và nghỉ là 3 giờ. Ta có phương trình:

$\frac{15}{x + 3} + \frac{15}{x - 3} + \frac{1}{3} = 3 \Leftrightarrow \frac{15}{x + 3} + \frac{15}{x - 3} = \frac{8}{3}$

$\Leftrightarrow 45 (x + 3) + 45 (x - 3) = 8 (x + 3) (x - 3)$

$\Leftrightarrow 45 x + 135 + 45 x - 135 = 8 (x^{2} - 9)$

$\Leftrightarrow 8 x^{2} - 90 x - 72 = 0 \Leftrightarrow 4 x^{2} - 45 x - 36 = 0$ .

$△ = 2025 + 576 = 2610, \sqrt{△} = 51$ .

Vậy $x_{1} = \frac{45 + 51}{2.4} = 12; x_{2} = \frac{45 - 51}{2.4} = \frac{- 3}{4}$ (loại).

Vậy vận tốc của ca nô khi nước yên lặng là 12 km/h.

Câu 2:

Một đội xe theo kể hoạch chở hết 140 tấn hàng trong một số ngày quy định. Do mỗi ngày đội đó chử vượt mức 5 tấn nên đội đã hoàn thành kế hoạch sớm hơn thời gian quy định 1 ngày và chở thêm được 10 tấn. Hỏi theo kế hoạch đội xe chở hàng hết bao nhiêu ngày?

Xem đáp án

Gọi số ngày theo kế hoạch đội xe chở hết hàng là x (ngày) (Điều kiện $x \in N *$ )

Theo kế hoạch mỗi ngày đội xe chở là: 140 : x = $\frac{140}{x}$ (tấn hàng).

Số ngày thực tế đội xe chở hàng là: x - 1 (ngày)

Thực tế đội xe chở được là: 140 + 10 = 150 (tấn hàng).

Theo thực tế mỗi ngày đội xe chở là:

$150 : (x - 1) = \frac{150}{x - 1}$ (tấn hàng).

Theo giả thiết, ta có phương trình:

$\frac{150}{x - 1} - \frac{140}{x} = 5 \Leftrightarrow \frac{30}{x - 1} - \frac{28}{x} = 1$

$\Leftrightarrow 30 x - 28 x + 28 = x^{2} - x \Leftrightarrow x^{2} - 3 x - 28 = 0$

$△ = 9 + 112 = 121, \sqrt{△} = 11$ .

Suy ra $x_{1} = \frac{3 + 11}{2} = 7$ (nhận); $x_{2} = \frac{3 - 11}{2} = - 4$ (loại).

Vậy theo kế hoạch đội xe chở hết hàng trong 7 ngày

Câu 3:

Một người đi xe đạp từ địa điểm A đến địa điểm B dài 30km. Khi đi ngược trở lại từ B về A người đó tăng vận tốc thêm 3 km/h nên thời gian về ngắn hơn thời gian đi là 30 phút. Tính vận tốc của người đi xe đạp lúc đi từ A đến B.

Xem đáp án

Gọi vận tốc của người đi xe đạp khi đi từ A đến B là x (km/h) (Điều kiện x > 0).

Thời gian đi từ A đến B là: 30 : x = $\frac{30}{x}$ (h).

Vận tốc của người đi từ B đến A là: x + 3 (km/h).

Thời gian đi từ B về A là: 30 : (x + 3) = $\frac{30}{x + 3}$ (h).

Thời gian về ít hơn thời gian đi là 30 phút = $\frac{1}{2}$ h nên ta có phương trình:

$\frac{30}{x} - \frac{30}{x + 3} = \frac{1}{2} \Leftrightarrow 60 (x + 3) - 60 x = x (x + 3)$

$\Leftrightarrow 60 x + 180 - 60 x = x^{2} + 3 x \Leftrightarrow x^{2} + 3 x - 180 = 0$

$△ = 9 + 720 = 729, \sqrt{△} = 27$ .

Vậy $x_{1} = \frac{- 3 + 27}{2} = 12$ (nhận); $x_{2} = \frac{- 3 - 27}{2} = - 15$ (loại).

Vậy vận tốc của người đi xe đạp khi đi từ A đến B là 12 km/h.

Câu 4:

Một nhóm công nhân đặt kế hoạch sản xuất 200 sản phẩm. Trong 4 ngày đầu họ thực hiện đúng mức đề ra, những ngày còn lại họ đã làm vượt mức mỗi ngày 10 sản phẩm, nên đã hoàn thành kế hoạch sớm 2 ngày. Hỏi theo kế hoạch mỗi ngày nhóm công nhân cần sản xuất bao nhiêu sản phẩm?

Xem đáp án

Thời gian hoàn thành theo kế hoạch là $\frac{200}{x}$ (ngày).

Sản phẩm làm trong 4 ngày đầu là 4x (sản phẩm).

Số sản phẩm những ngày còn lại phải làm là: 200 - 4x (sản phẩm).

Số sản phẩm mỗi ngày nhóm công nhân cần sản xuất trong những ngày còn lại là x + 10 (sản phẩm).

Thời gian hoàn thành số sản phẩm còn lại là: $\frac{200 - 4 x}{x + 10}$ (sản phẩm).

Theo giả thiết ta có phương trình:

$\frac{200}{x} - (\frac{200 - 4 x}{x + 10} + 4) = 2 \Leftrightarrow \frac{200}{x} - \frac{200 - 4 x}{x + 10} = 6$

$\Leftrightarrow \frac{100}{x} - \frac{100 - 2 x}{x + 10} = 3 \Leftrightarrow 100 x + 1000 - 100 x + 2 x^{2} = 3 x^{2} + 30 x$

$\Leftrightarrow x^{2} + 30 x - 1000 = 0$

$△' = 225 + 1000 = 1225, \sqrt{△'} = 35$ .

Vậy $x_{1} = \frac{- 15 + 35}{1} = 20$ (nhận); $x_{2} = \frac{- 15 - 35}{1} = - 50$ (loại).

Vậy theo kế hoạch mỗi ngày nhóm công nhân cần sản xuất 20 sản phẩm.

Câu 5:

Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình:

Hai người cùng làm chung một công việc trong $\frac{12}{5}$ giờ thì xong. Nếu mỗi người làm một mình thì người thứ nhất hoàn thành công việc trong ít hơn người thứ hai là 2 giờ. Hỏi nếu làm một mình thì mỗi người phải làm trong bao nhiêu thời gian để xong công việc?

Xem đáp án

Gọi thời gian người thứ nhất làm một mình xong công việc là x (giờ).

Điều kiện (x > $\frac{12}{5}$ ).

Thời gian người thứ hai làm một mình xong công việc là x + 2 (giờ).

Trong 1 giờ, người thứ nhất làm được: 1 : x = $\frac{1}{x}$ (công việc).

Trong 1 giờ, người thứ hai làm được: 1 : (x + 2) = $\frac{1}{x + 2}$ (công việc).

Trong 1 giờ, hai người làm chung được: $\frac{1}{x} + \frac{1}{x + 2}$ (công việc) hay $1 : \frac{12}{5} = \frac{5}{12}$ (công việc).

Ta có phương trình:

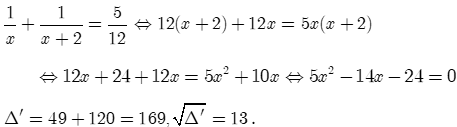
Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình: Hai người cùng làm chung một công (ảnh 1)

Ta có:

x_{1} = \frac{7 + 13}{5} = 4

(thích hợp),

x_{2} = \frac{7 - 13}{5} = \frac{- 6}{5}

(loại).

Vậy thời gian ngồi thứ nhất làm một mình xong công việc là 4 giờ.

Thời gian người thứ hai làm một mình xong công việc là: 4 + 2 = 6 (giờ).

Câu 6:

Hai ô tô đi từ A đến B dài 200km. Biết vận tốc xe thứ nhất nhanh hơn vận tốc xe thứ hai là 10km/h nên xe thứ nhất đến B sớm hơn xe thứ hai 1 giờ. Tính vận tốc mỗi xe

Xem đáp án

Gọi vận tốc xe thứ hai là x (km/h) (Điều kiện x > 0)

Vận tốc xe thứ nhất là x + 10 (km/h).

Thời gian xe thứ nhất đi từ A đến B là: 200 : (x + 10) = $\frac{200}{x + 10}$ (h)

Thời gian xe thứ hai đi từ A đến B là: 200 : x = $\frac{200}{x}$ (h)

Xe thứ nhất đến B sớm hơn xe thứ hai 1 giờ, nên ta có phương trình

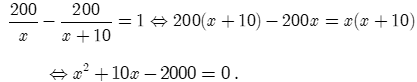Hai ô tô đi từ A đến B dài 200km. Biết vận tốc xe thứ nhất nhanh hơn vận tốc xe thứ (ảnh 1)

.

$△' = 25 + 2000 = 2025, \sqrt{△'} = 45$ .

Vậy $x_{1} = \frac{- 5 + 45}{1} = 40$ (nhận), $x_{2} = \frac{- 5 - 45}{1} = - 50$ (loại).

Vậy vận tốc xe thứ hai là 40km/h.

Vận tốc xe thứ nhất là 40 + 10 = 50 (km/h).

Câu 7:

Trên quãng đường AB dài 210km, tại cùng một thời điểm, một xe máy khởi hành từ A đi về B và một ô tô khởi hành từ B đi về A. Sau khi gặp nhau xe máy đi tiếp 4 giờ nữa thì đến B và ô tô đi tiếp 2 giờ 15 phút nữa thì đến A. Biết rằng xe máy và ô tô không thay đổi vận tốc trên suốt chặng đường. Tính vận tốc của xe máy và của ô tô.

Xem đáp án

Đổi 2 giờ 15 phút = $\frac{9}{4}$ giờ.

Gọi vận tốc của xe máy là x (km/h), vận tốc của ô tô là y (km/h) (Điều kiện x > 0, y > 0)

Xe máy đi trong 4 giờ được 4x (km), xe ô tô đi trong $\frac{9}{4}$ giờ được $\frac{9}{4}$ y (km).

Ta có phương trình $4 x + \frac{9}{4} y = 210$ (1)

Thời gian từ khi khởi hành đến lúc gặp nhau là

4x : y = $\frac{4 x}{y}$ (h) hay $\frac{9}{4} y : x = \frac{9 y}{4 x}$ (h).

Ta có phương trình: $\frac{4 x}{y} = \frac{9 y}{4 x}$ (2)

Từ (1) và (2), ta có hệ phương trình:

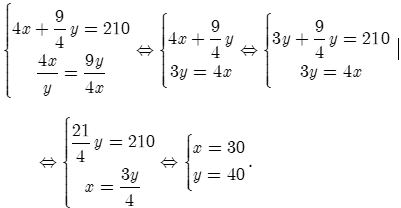
Trên quãng đường AB dài 210km, tại cùng một thời điểm, một xe máy khởi hành từ A đi về B và (ảnh 1)

Vậy vận tốc của xe máy là 30 km/h, vận tốc của ô tô là 40 km/h.

Câu 8:

Trong một giải bóng đá có 12 đội tham dư, thi đấu vòng tròn một lượt (hai đội bất kì thi đấu với nhau đúng một trận).

a) Chứng minh rằng sau 4 vòng đấu (mỗi đội thi đấu đúng 4 trận) luôn tìm được ba đội bóng đôi một chưa thi đấu với nhau.

Xem đáp án

Có 12 đội, mỗi đội thi đấu đúng 4 trận nên tìm được hai đội chưa thi đấu với nhau, gọi hai đội đó là A và B.

Mỗi đội A,B thi đấu đúng 4 trận, do vậy trong 10 đội còn lại có ít nhất 2 đội chưa thi đấu với cả A và B. Gọi một trong hai đội đó là C. A,B,C là ba đội bóng đôi một chưa thi đấu với nhau.

Câu 9:

b) Khẳng định trên còn đúng không nếu các đội đã thi đấu 5 trận?

Xem đáp án

Chẳng hạn: Chúng ta chia 12 đội thành hai nhóm, mỗi nhóm 6 đội, các đội trong mỗi nhóm đôi một đã thi đấu với nhau. Như vậy 12 đội bóng này, mỗi đội đã thi đấu đúng 5 lần.

Xét ba đội bóng tuỳ ý, luôn có 2 đội bóng ở cùng một nhóm. Như vậy ba đội bóng bất kì, có ít nhất hai đội đã thi đấu với nhau.

Câu 10:

Một phòng họp có 360 chỗ ngồi và được chia thành các dãy có số chỗ ngồi bằng nhau. Nếu thêm cho mỗi dãy 4 chỗ ngồi và bớt đi 3 dãy thì số chỗ ngồi trong phòng không thay đổi. Hỏi ban đầu số chỗ ngồi trong phòng họp được chia thành bao nhiêu dãy?

Xem đáp án

Gọi x (dãy) là số ghế lúc đầu được chia từ số chỗ ngồi trong phòng họp.

Điều kiện: $x \in N *$ và x > 3.

Số chỗ ngồi ở mỗi dãy lúc đầu: $\frac{360}{x}$ (chỗ).

Do thêm cho mỗi dãy 4 chỗ ngồi va bớt đi 3 dãy thì số chỗ ngồi trong phòng không thay đổi nên ta có phương trình:

Vậy lúc đầu số chỗ ngồi trong phòng họp được chia thành 18 dãy.

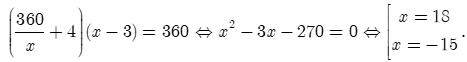
Câu 11:

Giải bài toán sau bằng cách lập phương trình:

Quãng đường từ A đến B dài 90km. Một người đi xe máy từ A đến B. Khi đến B, người đó nghỉ 30 phút rồi quay trở về A với vận tốc lớn hơn vận tốc lúc đi là 9km/h. Thời gian kể từ lúc bắt đầu đi từ A đến lúc trở về đến A là 5h. Tính vận tốc xe máy lúc đi từ A đến B.

Xem đáp án

Gọi vận tốc xe máy lúc đi từ A đến B là x (km/h).

Vận tốc xe máy đi từ B đến A là: x + 9 (km/h).

Thời gian xe máy đi từ B đến A là: 90 : x = $\frac{90}{x}$ (h).

Tổng thời gian xe máy đi từ A đến B, từ B về A (không kể thời gian nghỉ) là: 5 giờ - 30 phút = $\frac{9}{2}$ (giờ).

Ta có phương trình:

Vậy $x_{1} = \frac{31 + 41}{2} = 36$ (nhận), $x_{2} = \frac{31 - 41}{2} = - 5$ (loại).

Vậy vận tốc xe máy lúc đi từ A đến B là 36 km/h.

Câu 12:

Một tổ công nhân dự định làm xong 240 sản phẩm trong một thời gian nhất định. Nhưng khi thực hiện, nhờ cải tiến kĩ thuật nên mỗi ngày tổ đã làm tăng thêm 10 sản phẩm so với dự định. Do đó tổ đã hoàn thành sớm công việc sớm hơn dự định 2 ngày. Hỏi khi thực hiện, mỗi ngày tổ đã làm được bao nhiêu sản phẩm?

Xem đáp án

Gọi số sản phẩm mỗi ngày tổ đã làm là x (sản phẩm) (Điều kiện x > 0, x $\in N$ ).

Số sản phẩm mỗi ngày tổ dự định làm là x - 10 (sản phẩm)

Thời gian tổ hoàn thành công việc theo dự định là:

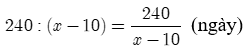
Một tổ công nhân dự định làm xong 240 sản phẩm trong một thời gian nhất định. Nhưng khi (ảnh 1)

Thời gian tổ hoàn thành công việc theo thực tế là: 240 : x = $\frac{240}{x}$ (ngày).

Theo giả thiết, ta có phương trình:

$△' = 25 + 1200 = 1225, \sqrt{△'} = 35$

Vậy $x_{1} = \frac{5 + 35}{1} = 40$ (sản phẩm), $x_{2} = \frac{5 - 35}{1} = - 30$ (loại).

Vậy số sản phẩm mỗi ngày tổ đã làm là 40 sản phẩm.

Câu 13:

Một mảnh vườn hình chữ nhật có chu vi 100m. Nếu tăng chiều rộng 3m và giảm chiều dài 4m thì diện tích mảnh vườn giảm xuống 2. Tính diện tích của mảnh vườn.

Xem đáp án

Gọi chiều rộng của mảnh vườn là x (m) (điều kiện 0 < x < 25)

Chiều dài của mảnh vườn là: 100 : 2 - x = 50 - x (m).

Diện tích của mảnh vườn là: x(50 - x) ( $m^{2}$ ).

Chiều rộng của mảnh vườn nếu tăng thêm 3m là: x + 3 (m).

Chiều dài của mảnh vườn nếu giảm 4m là: 50 - x - 4 = 46 - x (m).

Diện tích mới của mảnh vườn là: (x + 3)(46 - x) ( $m^{2}$ )

Theo giả thiết ta có phương trình:

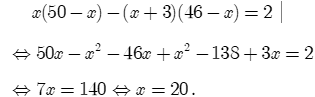
x = 20 thỏa mãn điều kiện. Vậy chiều rộng của mảnh vườn là 20 (m).

Chiều dài của mảnh vườn là: 50 - 20 = 30 (m).

Diện tích của mảnh vườn là: 20.30 = 600 ( $m^{2}$ ).

Câu 14:

Có hai vòi nước A, B cùng cung cấp cho một hồ cạn nước và vòi C (đặt sát đáy hồ) lấy nước từ hồ cung cấp cho hệ thống tưới cây. Đúng 6 giờ vòi A và B được mở; đến 7 giờ vòi C được mở; đến 9 giờ thì sống vòi B và vòi C; đến 10 giờ 45 phút thì hồ đầy nước. Người ta thấy rằng nếu đóng vòi B ngay từ đầu thì phải đến đúng 13 giờ hồ mới đầy. Biết lưu lượng vòi B là trung bình cộng của vòi A và vòi C, hỏi một mình vòi C tháo cạn hồ nước đầy trong bao lâu?

Xem đáp án

10 giờ 45 phút = $\frac{43}{4}$ (giờ)

Gọi thời gian để vòi A,B chảy riêng vào đầy bể lần lượt là x (giờ), y (giờ), thời gian để vòi C tháo cạn hồ nước đầy là z (giờ). (Điều kiện x,y,z > 0).

Trong 1 giờ vòi A chảy vào được $\frac{1}{x}$ (hồ), vòi B chảy vào được $\frac{1}{y}$ (hồ), vòi C tháo ra $\frac{1}{z}$ (hồ).

Đúng 6 giờ, A và B mở, đến 7 giờ C mở, đến 9 giờ thì đóng B,C , đến 10 giờ 45 phút thì hồ đầy. Ta có:

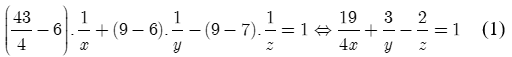
Có hai vòi nước A, B cùng cung cấp cho một hồ cạn nước và vòi C (đặt sát đáy hồ) lấy nước (ảnh 1)

Nếu đóng B ngay từ đầu đến 13 (h) hồ đầy nên

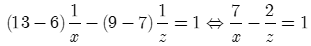Có hai vòi nước A, B cùng cung cấp cho một hồ cạn nước và vòi C (đặt sát đáy hồ) lấy nước (ảnh 2)

(2)

Lưu lượng vòi B là trung bình cộng của lưu lượng vòi A và vòi C nên:

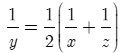(3)

Từ (1), (2), (3) ta có:

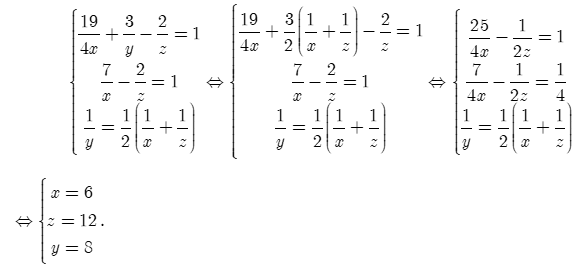
Có hai vòi nước A, B cùng cung cấp cho một hồ cạn nước và vòi C (đặt sát đáy hồ) lấy nước (ảnh 4)

Vậy một mình vòi C tháo cạn hồ nước đầy trong 12 giờ.

Câu 15:

Một người đi xe đạp từ A đến B cách nhau 36 km. Khi đi từ B trở về A, người đó tăng vận tốc thêm 3km/h, vì vậy thời gian về ít hơn thời gian đi là 36 phút. Tính vận tốc của người đi xe đạp khi đi từ A đến B.

Xem đáp án

Gọi x (km/h) là vận tốc của người đi xe đạp khi đi từ A đến B (x > 0).

Thời gian của người đi xe đạp khi đi từ A đến B là $\frac{36}{x}$ .

Vận tốc của người đi xe đạp khi đi từ A đến B là x + 3.

Thời gian của người đi xe đạp khi đi từ B đến A là $\frac{36}{x + 3}$ .

Theo giả thiết ta có phương trình: $\frac{36}{x} - \frac{36}{x + 3} = \frac{36}{60}$ .

Giải phương trình ta được hai nghiệm $\{\begin{cases} x = 12 \\ x = - 15 & (l o a i) \end{cases}$

Vậy vận tốc của người đi xe đạp khi đi từ A đến B là 12 (km/h).

Câu 16:

Trên quãng đường AB dài 60km, người thứ nhất đi xe máy từ A đến B, người thứ hai đi xe đạp từ B đến A. Họ khởi hành cùng một lúc và gặp nhau tại C sau khi khởi hành được 1 giờ 20 phút. Từ C người thứ nhất đi tiếp đến B và người thứ hai đi tiếp đến A. Kết quả người thứ nhất đến nơi sớm hơn người thứ hai là 2 giờ. Tính vận tốc của mỗi người, biết rằng trên suốt quãng đường cả hai người đều đi với vận tốc không đổi

Xem đáp án

Gọi vận tốc của người thứ nhất là x km/h, (x > 0).

Gọi vận tốc của người thứ hai là y km/h, (y > 0).

Đổi 1 giờ 20 phút = $\frac{4}{3}$ giờ $\Rightarrow \frac{4}{3} (x + y) = 60 \Rightarrow x + y = 45$ .

Theo giả thiết ta có hệ phương trình: $\{\begin{cases} x + y = 45 \\ \frac{60}{x} + 2 = \frac{60}{y} \end{cases}$

Giải hệ phương trình ta được: x = 30, y = 15.

Vậy vận tốc của người thứ nhất là 30 (km/h), vận tốc người thứ hai là 15 (km/h).

Câu 17:

Trong một kì thi, 60 thí sinh phải giải 3 bài toán. Khi kết thúc kì thi, người ta nhận thấy rằng: với hai thí sinh bất kì luôn có ít nhất một bài toán mà cả hai thí sinh đó đều giải được. Chứng minh rằng:

a) Nếu có một bài toán mà mọi thí sinh đều không đạt giải được thì phải có một bài toán khác mà mọi thí sinh đều giải được

Xem đáp án

Không mất tính tổng quát, giả sử mọi thí sinh đều không giải được bài toán A.

- Nếu mọi thí sinh đều không giải được bài toán B thì từ giả thiết ta có mọi thí sinh đều giải được bài toán C.

- Nếu mọi thí sinh đều giải được bài toán B và bài toán C thì ta có mọi thí sinh đều giải được bài toán B, bài toán C.

- Nếu có một thí sinh chỉ giải được một bài toán, giả sử giải được bài toán B. Xét học sinh này với tất cả các học sinh còn lại. Theo giả thiết, có mọi thí sinh đều giải được bài toán B.

Vậy nếu có một bài toán mà mọi thí sinh đều không giải được thì phải có một bài toán khác mà mọi thí sinh đều giải được.

Câu 18:

b) Có một bài toán mà có ít nhất 40 thí sinh giải được.

Gọi ba bài toán là A,B,C.

Xem đáp án

Theo giả thiết ta có mọi thí sinh đều giải được ít nhất một bài toán. Nếu có một thí sinh chỉ giải đúng một bài toán, xét học sinh này với tất cả các học sinh còn lại, ta có mọi thí sinh đều giải được bài toán đó. Ta chỉ còn xét trường hợp mà mọi thí sinh giải được ít nhất hai bài toán.

Gọi số thí sinh giải được A,B mà không giải được C là x, số thí sinh giải được B,C mà không giải được A là y, số thí sinh giải được A,C mà không giải được B là z, số thí sinh giải được cả A,B,C là t.

Ta có: x + y + z + t = 60 (1)

Cách 1

Giả sử có điều trái với kết luận của bài toán.

Ta có: x + z + t < 40; x + y + t < 40; y + z + t < 40.

Do đó: x + z + t + x + y + t + y + z + t < 40 + 40 + 40

2(x + y + z + t) + t < 120

Kết hợp (1) có t <0. Điều này vô lí! Điều giả sử trên là sai.

Vậy có một bài toán mà có ít nhất 40 thí sinh giải được.

Cách 2

Ta có số học sinh không giải được A là y, không giải được B là z, không giải được C là x.

Nếu x > 20, y > 20, z > 20 thì x + y + z > 60. Mâu thuẫn (1).

Do đó trong ba số x, y, z phải có một số không vượt quá 20.

Như vậy có một bài toán mà có nhiều nhất 20 thí sinh không giải được. Do đó bài toán này có ít nhất 40 thí sinh giải được.

Vậy có một bài toán mà có ít nhất 40 thí sinh giải được.

Câu 19:

Một ô tô và một xe máy ở hai địa điểm A và B cách nhau 180 km, khởi hành cùng một lúc đi ngược chiều nhau và gặp nhau sau 2 giờ. Biết vận tốc của ô tô lớn hơn vận tốc của xe máy 10km/h. Tính vận tốc của mỗi xe.

Xem đáp án

Gọi vận tốc của ô tô là x (km/h).

Vận tốc của xe máy là y (km/h) (Điều kiện: x > y > 0, x > 10).

Ta có phương trình: x - y = 10 (1)

Sau 2 giờ ô tô đi được quãng đường là 2x (km).

Sau 2 giờ xe máy đi được quãng đường là 2y (km) thì chúng gặp nhau, ta có phương trình: 2x + 2y = 180 hay x + y = 90 (2)

Từ (1) và (2) ta có hệ phương trình:

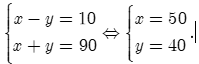
Một ô tô và một xe máy ở hai địa điểm A và B cách nhau 180 km, khởi hành cùng một lúc đi (ảnh 1)

.Vậy vận tốc của ô tô là 50 km/h và vận tốc của xe máy là: 40 km/h.

Câu 20:

Một phân xưởng theo kế hoạch cần phải sản xuất 1100 sản phẩm trong một số ngày quy định. Do mỗi ngày phân xưởng đó sản xuất vượt mức 5 sản phẩm trên phân xưởng đã hoàn thành kế hoạch sớm hơn thời gian quy định 2 ngày. Hỏi theo kế hoạch, mỗi ngày phân xưởng phải sản xuất bao nhiêu sản phẩm?

Xem đáp án

Gọi số sản phẩm phân xưởng làm một ngày theo kế hoạch là x (sản phẩm) (Điều kiện: $x \in N *$ )

Số sản phẩm phân xưởng làm mỗi ngày theo thực tế là x + 5 (sản phẩm).

Theo kế hoạch phân xưởng sản xuất 1100 sản phẩm trong

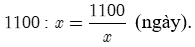
Thực tế phân xưởng hoàn thành kế hoạch trong:

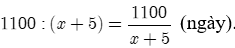
Theo giả thiết, ta có phương trình:

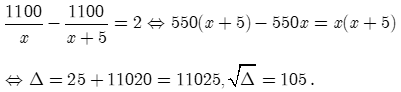
Giải phương trình ta được:

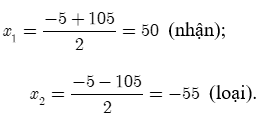
Một phân xưởng theo kế hoạch cần phải sản xuất 1100 sản phẩm trong một số ngày quy định (ảnh 4)

Vậy theo kế hoạch mỗi ngày phân xưởng làm được 50 sản phẩm.

Câu 21:

Cho mảnh vườn hình chữ nhật có diện tích 360( $m^{2}$ ). Nếu tăng chiều rộng 2m và giảm chiều dài 6m thì diện tích không thay đổi. Tính chu vi của mảnh vườn lúc ban đầu.

Xem đáp án

Gọi chiều rộng của mảnh vườn là x (m) (điều kiện x > 0)

Chiều dài của mảnh vườn là: 360 : x = $\frac{360}{x}$ (m)

Chiều rộng mảnh vườn sau khi tăng 2m là: x + 2(m)

Chiều dài mảnh vườn sau khi giảm 6m là: $\frac{360}{x} - 6$ (m)

Diện tích mảnh vườn nếu tăng chiều rộng 2m và giảm chiều dài đi 6m là: $(x + 2) (\frac{360}{x} - 6) (m^{2})$ .

Theo giả thiết ta có phương trình:

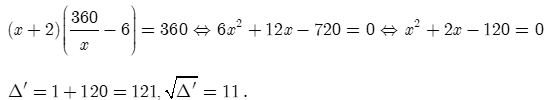
Vậy $x_{1} = \frac{- 1 + 11}{1} = 10$ (nhận), $x_{2} = \frac{- 1 - 11}{1} = - 12$ (loại).

Chiều rộng của mảnh vườn là 10m

Chiều dài của mảnh vườn là $\frac{360}{10} = 36$ (m)

Chu vi của mảnh vườn là: (10 + 36).2 = 92 (m).

Câu 22:

Cho quãng đường AB dài 120km. Lúc 7 giờ sáng, một xe máy đi từ A đến B Đi được $\frac{3}{4}$ quãng đường xe bị hỏng phải dừng lại sửa mất 10 phút rồi đi tiếp đến B với vận tốc nhỏ hơn vận tốc lúc đầu 10km/h. Biết xe máy đến B lúc 11 giờ 40 phút trưa cùng ngày. Giả sử vận tốc của xe máy trên $\frac{3}{4}$ quãng đường ban đầu không thay đổi và vận tốc của xe máy trên $\frac{1}{4}$ quãng đường còn lại cũng không thay đổi. Hỏi xe máy bị hỏng lúc mấy giờ?

Xem đáp án

Gọi C là vị trí xe máy bị hỏng.

Quãng đường AC dài là: 120. $\frac{3}{4}$ = 90 (km).

Quãng đường CB dài là: 120 - 90 = 30 (km).

Gọi vận tốc xe máy đi trên quãng đường AC là: x (km/h) (Điều kiện x > 10)

Vận tốc xe máy đi trên quãng đường CB là x -10 (km).

Thời gian xe máy đi trên quãng đường AC là: 90 : x = $\frac{90}{x}$

Thời gian xe máy đi trên quãng đường CB là

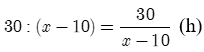
Đổi 10 phút = $\frac{1}{6}$ (h)

Thời gian xe máy đi từ A đến B (kể cả thời gian sửa xe) là:

11 giờ 40 phút - 7giờ = $\frac{14}{3}$ (h)

Theo giả thiết, ta có phương trình:

$x_{1} = \frac{55 + 35}{3} = 30$ (nhận), $x_{2} = \frac{55 - 35}{3} = \frac{20}{3}$ (loại).

Vận tốc xe máy đi trên quãng đường AC là 30 (km/h).

Thời gian xe máy đi từ A đến C là $\frac{90}{30}$ (h).

Vậy xe máy bị hỏng lúc: 7 + 3 = 10 (h) (trưa cùng ngày).

Câu 23:

Tổng kết học kì II, trường trung học cơ sở N có 60 học sinh không đạt học sinh giỏi, trong đó có 6 em từng đạt học sinh giỏi trong học kì I; số học sinh giỏi học kì II bằng $\frac{40}{37}$ số học sinh giỏi học kì I và có 8% số học sinh của trường không đạt học sinh giỏi học kì I nhưng đạt học sinh giỏi học kì II. Tìm số học sinh giỏi học kì II của trường biết rằng số học sinh của trường không thay đổi trong suốt năm học.

Xem đáp án

Gọi x là số học sinh của trường (x $\in N, x > 60$ ).

Khi đó, số học sinh giỏi ở học kì II là x - 60.

Số học sinh giỏi ở học kì I là x - 60 + 6 - 8%x = $\frac{23}{25} x - 54$ .

Theo giả thiết, ta có phương trình:

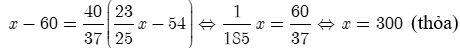
Vậy số học sinh giỏi học kì II là: 300 - 60 = 240 (học sinh).

Câu 24:

Kì thi tuyển sinh vào trường THPT chuyên Long An năm nay có 529 học sinh đến từ 16 địa phương khác nhau tham dự. Gỉa sử điểm bài thi môn Toán của mỗi học sinh đều là số nguyên dương lớn hơn 4 và bé hơn hoặc bằng 10. Chứng minh rằng luôn tìm được 6 học sinh có điểm môn Toán giống nhau và cùng đến từ một địa phương.

Xem đáp án

Ta có 529 học sinh có điểm bài thi 5 điểm đến 10 điểm. Theo nguyên lí Dirichlet ta có 89 học sinh có điểm bài thi như nhau (từ 5 điểm đến 10 điểm).

Ta có 89 học sinh có điểm bài thi như nhau và đến từ 16 địa phương. Theo nguyên lí Dirichlet tìm được 6 em có cùng điểm thi môn toán và đến từ cùng một địa phương

Câu 25:

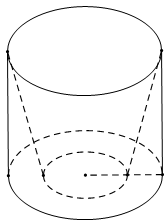
Một cái xô bằng I - nốc có dạng hình nón cụt (độ dày của thành xô nhỏ không đáng kể) đựng hóa chất được đặt vào bên trong một cái thùng hình trụ, có miệng xô trùng khít với miệng thùng. Đáy xô dát với đáy thùng và có bán kính bằng $\frac{1}{2}$ bán kính đáy thùng.
Biết rằng, thùng có nhiều cao bằng đường kính đáy và diện tích xung quanh bằng $8 π ({dm}^{2})$ . Hỏi khi xô chứa đầy hóa chất thì dung tích của nó là bao nhiêu lít? (cho p $\approx$ 3,14 và kết quả làm tròn đến chữ số thập phân thứ nhất).

Một cái xô bằng I - nốc có dạng hình nón cụt (độ dày của thành xô nhỏ không đáng kể) đựng (ảnh 1)

Xem đáp án

Gọi R (dm) là bán kính của đáy thùng.

Thùng hình trụ có bán kính đáy bằng R và chiều cao h = 2R nên
diện tích xung quanh của nó là:

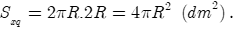
Nên $4 {πR}^{2} = 8 π \Leftrightarrow R^{2} = 2 \Rightarrow \sqrt{R} = 2 (dm)$ (dm).

Xô có đáy hình nón cụt có hai đáy lần lượt là:

$R_{1} = R = \sqrt{2}$ (dm) và $R_{2} = \frac{1}{2} R = \frac{\sqrt{2}}{2}$ (dm).

Từ đó ta có chiều cao của xô là: h = 2R = 2 $\sqrt{2}$ (dm).

Nên

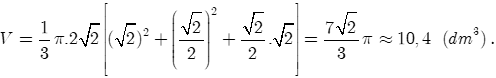
Vậy khi xô chứa đầy hóa chất thì dung tích của nó là 10,4 (lít).

Câu 26:

Một đội xe cần chở 36 tấn hàng. Trước khi làm việc, đội được bổ sung thêm 3 chiếc nữa nên mỗi xe chở ít hơn 1 tấn hàng so với dự định. Hỏi lúc đầu đội có bao nhiêu xe, biết khối lượng hàng chở trên mỗi xe như nhau

Xem đáp án

Gọi số xe ban đầu của mỗi xe có là x (xe) (Điều kiện $x \in N *$ ).

Số xe lúc sau có là x + 3 (xe).

Lúc đầu mỗi xe dự định chở là: 36 : 6 = $\frac{36}{6}$ (tấn).

Lúc sau mỗi xe chở là: 36 : (x + 3) = $\frac{36}{x + 3}$ (tấn).

Theo giả thiết ta có phương trình: $\frac{36}{x} - \frac{36}{x + 3} = 1$ .

Phương trình tương đương với

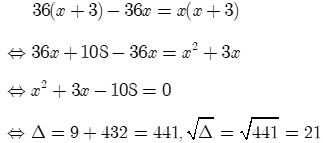
Vậy $x_{1} = \frac{- 3 + 21}{2} = 9$ (nhận); $x_{1} = \frac{- 3 - 21}{2} = - 12$ (loại).

Câu 27:

Với sự phát triển của khoa học kỹ thuật hiện nay, người ta tạo ra nhiều mẫu xe lăn đẹp và tiện dụng cho người khuyết tật. Công ty A đã sản xuất ra những chiếc xe lăn cho người khuyết tật với số vốn ban đầu là 500 triệu đồng. Chi phí sản để sản xuất ra một chiếc xe lăn là 2.500.000 đồng. Gía bán ra mỗi chiếc là 3.000.000 đồng.

a) Viết hàm số biểu diễn tổng số tiền đã đầu tư đến khi sản xuất ra được x chiếc xe lăn (gồm vốn ban đầu và chi phí sản xuất) và hàm số biểu diễn số tiền thu được khi bán ra x chiếc xe lăn.

Xem đáp án

Tổng chi phí vốn cố định và vốn sản xuất ra x chiếc xe lăn (đơn vị triệu đồng): y = 500 + 2.5x.

Hàm số biểu diễn số tiền thu được khi bán ra x chiếc xe lăn là: y = 3x.

Câu 28:

b) Công ty A phải bán bao nhiêu chiếc xe mới có thể thu hồi được vốn ban đầu

Xem đáp án

Để số tiền bán được và số vốn đầu tư ban đầu bằng nhau, ta có:

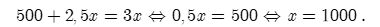
Vậy công ty A phải bán 1000 chiếc xe lăn mới thu hồi được vốn ban đầu.

Câu 29:

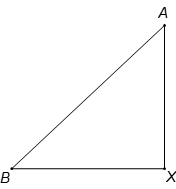
Trên một vùng biên được xem như bằng thẳng và không có chướng ngại vật. Vào lúc 6 giờ có một tàu cá đi thẳng hàng qua tọa độ X theo hướng từ Nam tới Bắc với vận tốc không đổi. Đến 7 giờ một tàu du lịch cũng đi thẳng qua tọa độ X theo hướng từ Đông sang Tây với vận tốc lớn hơn vận tốc tàu cá 12 km/h. Đến 8 giờ khoảng cách giữa hai tàu là 60 km/h. Tính vận tốc của mỗi tàu

Trên một vùng biên được xem như bằng thẳng và không có chướng ngại vật. Vào lúc 6 giờ có (ảnh 1)

Xem đáp án

Gọi vận tốc của tàu đánh cá là x (km/h). (Điều kiện x > 0).

Vận tốc của tàu du lịch là x + 12 (km/h).

Giả sử tàu đánh cá đến điểm A, tàu du lịch đến điểm B. Theo giả thiết, khoảng cách AB là 60km.

Tàu đánh cá đã đi: 8 - 6 = 2 (giờ).

Khoảng cách XA dài 2x (km).

Tàu du lịch đã đi: 8 - 7 = 1 (giờ).

Khoảng cách XB dài là: (x + 12).1 = x + 12 (km).

Theo giả thiết, ta có tam giác XAB vuông tại X.

Do đó $X A^{2} + X B^{2} = A B$ (định lí Pythagore).

Ta có phương trình:

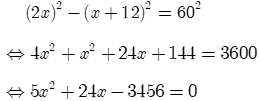
Xét biệt thức $△' = 144 + 17280 = 17424$ , $\sqrt{△'} = 132$ .

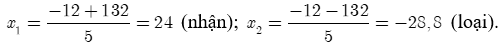
Vậy vận tốc của tàu đánh cá là 24 (km/h).

Vận tốc của tàu du lịch là: 24 + 12 = 36(km/h).

Câu 30:

Hai công nhân cùng làm chung trong 4 giờ thì xong một con đường. Nếu mỗi đội làm riêng để xong con đường thì thời gian đội thứ nhất ít hơn đội thứ hai là 6 giờ. Hỏi nếu làm riêng thì mỗi đội làm xong con đường trong thời gian bao lâu?

Xem đáp án

Gọi thời gian đội thứ nhất làm riêng xong công việc là x (giờ) (Điều kiện x > 0).

Thời gian đội thứ hai làm riêng xong công việc là x + 6 (giờ).

Trong 1 giờ:

Đội thứ nhất làm riêng được: 1 : x = $\frac{1}{x}$ (công việc)

Đội thứ hai làm riêng được: 1 : (x + 6) = $\frac{1}{x + 6}$ (công việc)

Hai đội làm chung được: 1 : 4 = $\frac{1}{4}$ (công việc).

Ta có phương trình:

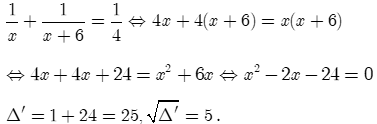
Vậy $x_{1} = 1 + 5 = 6$ (nhận); $x_{2} = 1 - 5 = - 4$ (loại).

Thời gian đội thứ nhất làm riêng xong công việc là 6 giờ.

Thời gian đội thứ hai làm riêng xong công việc là: 6 + 6 = 12 (giờ).

Câu 31:

Một tàu tuần tra chạy ngược dòng 60 km, sau đó chạy xuôi dòng 48 km trên cùng một dòng sông có vận tốc của dòng nước là 2 km/giờ. Tính vận tốc của tàu tuần tra khi nước yên lặng, biết thời gian xuôi dòng ít hơn thời gian ngược dòng 1 giờ

Xem đáp án

Gọi vận tốc của tàu tuần tra khi nước yên lặng là x (km/giờ) (Điều kiện x > 2).

Tàu tuần tra xuôi dòng với vận tốc x + 2 (km/giờ) và ngược dòng với vận tốc x - 2 (km/giờ).

Thời gian tàu tuần tra chạy xuôi dòng là:

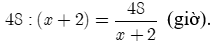
Thời gian tàu tuần tra chạy ngược dòng là:

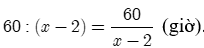
Theo giả thiết, ta có phương trình:

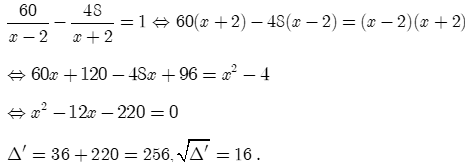
Ta có $x_{1} = \frac{6 + 16}{1} = 22$ (nhận), $x_{2} = \frac{6 - 16}{1} = - 10$ (loại).

Vậy vận tốc của tàu tuần tra khi nước yên lặng là 22 km/giờ.

Câu 32:

Số tiền mua 1 quả dừa và một quả thanh long là 25 nghìn đồng. Số tiền mua 5 quả dừa và 4 quả thanh long là 120 nghìn đồng. Hỏi giá mỗi quả dừa và mỗi quả thanh long là bao nhiêu? Biết rằng mỗi quả dừa có giá như nhau và mỗi quả thanh long có giá như nhau.

Xem đáp án

Gọi giá tiền mua 1 quả dừa là x (nghìn đồng), giá tiền mua 1 quả thanh long là y (nghìn đồng) (Điều kiện: x,y > 0).

Mua 1 quả dừa và 1 quả thanh long hết 25 nghìn đồng, ta có phương trình: x + y = 25 (1)

Mua 5 quả dừa và 4 quả thanh long hết 120 nghìn đồng, ta có phương trình: 5x + 4y = 120 (2)

Từ (1) và (2) ta có hệ phương trình:

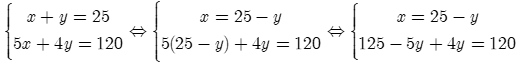
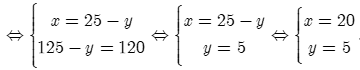
Vậy giá tiền mỗi quả dừa là 20 nghìn đồng, giá tiền mỗi quả thanh long là 5 nghìn đồng.

Câu 33:

Một mảnh vườn hình chữ nhật có diện tích là 168 $m^{2}$ . Nếu giảm chiều dài đi 1m và tăng chiều rộng thêm 1m thì mảnh vườn trở thành hình vuông. Tính chiều dài, chiều rộng của mảnh vườn.

Xem đáp án

Gọi chiều rộng mảnh vườn là x (m) (Điều kiện x > 0)

Chiều dài mảnh vườn là $\frac{168}{x}$ (m).

Nếu giảm chiều dài đi 1m thì cạnh đó còn là $\frac{168}{x} - 1$ (m), tăng chiều rộng thêm 1m thì cạnh đó là x + 1 (m), mảnh vườn trở thành hình vuông nên ta có phương trình: $\frac{168}{x} - 1 = x + 1$ .

Do đó ta có:

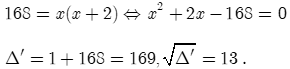
Vậy $x_{1} = \frac{- 1 + 13}{1} = 12$ (nhận), $x_{2} = \frac{- 1 - 13}{1} = - 14$ (loại).

Vậy mảnh vườn có chiều rộng là 12 m, chiều dài là

\frac{168}{12} = 14

(m).

Câu 34:

Một người vận động viên tham gia cuộc thi đấu quần vợt. Cứ hai người trong họ chơi với nhau đúng một trận. Người thứ nhất thắng $x_{1}$ trận và thua $y_{1}$ trận, người thứ hai thắng $x_{2}$ trận và thua $y_{2}$ trận, ..., người thứ mười thắng $x_{10}$ trận và thua $y_{10}$ trận. Biết rằng trong một trận đấu quần vợt không có kết quả hòa. Chứng minh rằng:

Xem đáp án

Mỗi người đều chơi 9 trận với 9 người khác và không có trận hòa. Do đó:

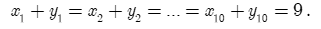
Mà tổng số trận thắng bằng tổng số trận thua, do đó:

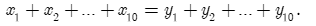
Ta có:

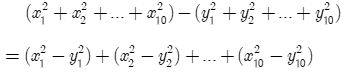
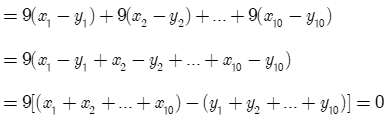
Vậy

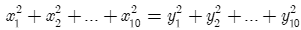
Câu 35:

Một xe tải đi từ A đến B với vận tốc 40 km/h. Sau khi xe tải xuất phát một thời gian thì một xe khách cũng xuất phát từ A với vận tốc 50 km/h và nếu không có gì thay đổi thì sẽ đuổi kịp xe tải tại B. Nhưng sau khi đi được một nửa quãng đường AB, xe khách tăng vận tốc lên 60 km/h nên đến B sớm hơn xe tải 16 phút. Tính quãng đường AB.

Xem đáp án

Gọi quãng đường AB dài là x (km), thời gian từ lúc xe tải xuất phát đến lúc xe khách xuất phát là y (giờ) (Điều kiện x,y > 0).

Đổi 16 phút $\frac{4}{15}$ giờ.

Thời gian xe tải đi từ A đến B là $\frac{x}{40}$ (h), thời gian xe khách đi từ A đến B với vận tốc 50 km/h là $\frac{x}{50}$ (h), ta có phương trình:

$\frac{x}{40} = y + \frac{x}{50}$ (1)

Thời gian thực tế xe khách đi $\frac{1}{2} . \frac{x}{5} + \frac{1}{2} . \frac{x}{60}$ (h), ta có phương trình:

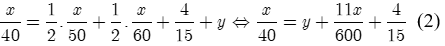
Một xe tải đi từ A đến B với vận tốc 40 km/h. Sau khi xe tải xuất phát một thời gian thì (ảnh 1)

Từ (1), (2) ta có hệ phương trình:

Vậy quãng đường AB dài 160 km

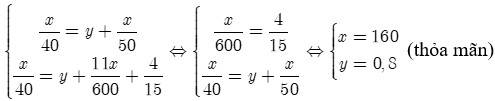
Câu 36:

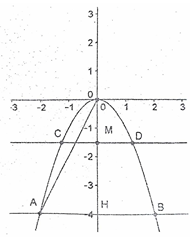
Một xe tải có chiều rộng 2,4m và chiều cao 2,5m muốn đi qua một cái cổng có hình parabol. Biết khoảng cách giữa hai chân cổng là 4m và khoảng cách từ đỉnh cổng (đỉnh parabol) tới mỗi chân cổng là 2 $\sqrt{5}$ m (bỏ qua độ dày của cổng).

1) Trong mặt phẳng tọa độ Oxy gọi parabol (P) y = ax² với a < 0 hình biểu diễn cổng mà xe tải muốn đi qua. Chứng minh a = -1.

Một xe tải có chiều rộng 2,4m và chiều cao 2,5m muốn đi qua một cái cổng có hình parabol (ảnh 1)

Xem đáp án

Đỉnh cổng là đỉnh của parabol y = ax² (a < 0), đỉnh cổng là O(0,0).

Gọi hai chân cổng là A,B. AB cắt Oy tại H.

Ta có:

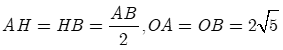
(A, B, H nằm dưới trục hoành).

$△$ HOA vuông tại H.

Suy ra OH² + AH² = OA² (định lí Pythagore)

$O H^{2} = {(2 \sqrt{5})}^{2} - 2^{2} = 16 \Rightarrow O H = 4$ .

Do đó H(0; -4). Nên A(-2; 4), B(2; -4).

A $\in (P)$ nên $- 4 = a {(- 2)}^{2} \Leftrightarrow a = - 1$ .

Câu 37:

2) Hỏi xe tải có thể đi qua cổng có được không? Tại sao?

Xem đáp án

Gọi giao điểm của đường thẳng đi qua điểm cao nhất của xe tải, song song với trục hoành với (P) là C, D, CD cắt Oy tại M.

Phương trình đường thẳng CD là y = 1,5.

Phương trình hoành độ giao điểm của (P) và CD.

$- x^{2} = 1, 5 \Leftrightarrow x = \pm \frac{\sqrt{6}}{2}$ .

Do đó CD = $\sqrt{6}$ . Mà $\sqrt{6}$ > 2,4.

Tại độ cao 2,5m thì chiều rộng của cổng là $\sqrt{6}$ lớn hơn 2,4m là chiều rộng của xe tải. Như vậy xe tải có thể qua cổng được.

Câu 38:

Bạn An dự định trong khoảng thời gian từ ngày 1/3 đến ngày 30/4 sẽ giải mỗi ngày 3 bài toán. Thực hiện đúng kế hoạch được một thời gian, vào khoảng cuối tháng 3 (tháng 3 có 31 ngày) thì An bị bênh, phải nghĩ giải toán nhiều ngày liên tiếp. Khi hồi phục, trong tuần đầu An chỉ giải được 16 bài; sau đó An cố gắng giải 4 bài mỗi ngày và đến 30/4 thì An cũng hoàn thành kế hoạch đã định. Hỏi bạn An phải nghỉ giải toán ít nhất bao nhiêu ngày?

Xem đáp án

Gọi số ngày An giải toán trước khi bệnh là x (ngày) (Điều kiện x $\in N *$ , x < 31) và số ngày An nghỉ giải toán là y (ngày) (Điều kiện y $\in$ N)

Thời gian từ ngày 1/3 đến ngày 30/4 là 31 + 30 = 61 (ngày).

Do vậy số bài toán An dự định giải là 3.61 = 183 (bài toán).

Theo giả thiết, ta có phương trình:

3x + 16 + 4.(61 - x - y - 7) = 183 $\Leftrightarrow$ -x - 4y + 232 = 183

$\Leftrightarrow 4 y = 49 - x \Leftrightarrow y = \frac{49 - x}{4}$

Mà x < 31. Do đó y > $\frac{49 - x}{4}$ = 4,5. Khi đó x = 49 - 4y = 29.

Vậy bạn An phải nghỉ giải toán ít nhất 5 ngày.

Câu 39:

Để khuyến khích phong trào học tập, một trường THCS đã tổ chức 8 đợt thi cho các học sinh. Ở mỗi đợt thi, có đúng 3 học sinh được chọn để trao giải. Sau khi tổ chức xong 8 đợt thi, người ta nhận thấy rằng với hai đợt thi bất kì luôn có đúng 1 học sinh được trao giải ở cả hai đợt thi đó. Chứng minh rằng:

a) Có ít nhất một học sinh được trao giải ít nhất bốn lần.

Xem đáp án

Xét đợt thi thứ nhất. Theo giả thiết có đúng 1 học sinh được trao giải trong hai đợt thi bất kì, vì vậy trong 7 đợt thi còn lại, trong ba học sinh được trao giải đợt thi thứ nhất có một học sinh được trao giải ít nhất 3 lần (vì 7 : 3 = 2 (dư ))

Vậy có một học sinh được trao giải ít nhất bốn lần.

Câu 40:

b) Có đúng một học sinh được trao giải ở tất cả 8 đợt thi.

Xem đáp án

Từ a) giả sử A là học sinh được trao giải ở bốn đợt thi. Xét một đợt thi bất kì trong bốn đợt thi còn lại. Vì có đúng một học sinh được trao giải trong hai đợt thi bất kì. Do vậy đợt thi này, bốn đợt thi mỗi đợt thi có một học sinh trao giải. Như vậy học sinh đó phải là A (nếu không là A thì đợt này có đến bốn học sinh được trao giải). Vì xét đợt thi bất kì nên A được trao giải trong bốn đợt thi còn lại.

A được trao giải ở tất cả 8 đợt thi.

Vậy có đúng một học sinh được trao giải ở tất cả 8 đợt thi.

Câu 41:

Trong một phòng có 80 người họp, được sắp xếp ngồi trên các dãy ghế có chỗ ngồi bằng nhau. Nếu ta bớt đi 2 dãy ghế thì mỗi dãy ghế còn lại phải xếp thêm 2 người thì vừa đủ chỗ. Hỏi lúc đầu có mấy dãy ghế và mỗi dãy ghế được xếp bao nhiêu chỗ ngồi

Xem đáp án

Gọi số dãy ghế lúc đầu là x (dãy ghế) (Điều kiện x $\in N *$ , x > 2)

Mỗi dãy ghế được xếp số chỗ ngồi là $\frac{80}{x}$ (chỗ ngồi).

Nếu bớt đi 2 dãy ghế thì còn x - 2 (dãy ghế) mỗi dãy ghế được xếp chỗ ngồi là $\frac{80}{x - 2}$ (chỗ ngồi).

Theo giả thiết, ta có phương trình $\frac{80}{x - 2} - \frac{80}{x} = 2$ .

Ta có

v

Vậy $x_{1} = \frac{1 + 9}{1} = 10$ (nhận), $x_{2} = \frac{1 - 9}{1} = - 8$ (loại).

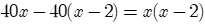
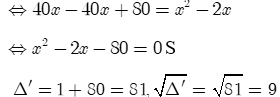Vậy số dãy ghế lúc đầu là 10 dãy.

Mỗi dãy ghế được xếp số chỗ ngồi là

\frac{80}{10} = 8

(chỗ ngồi).