6 câu hỏi trắc nghiệm thuộc Chủ đề 9: Dạng toán liên quan đến thửa ruộng và khu vườn

Câu 1:

Một khu vườn hình chữ nhật có chu vi 280m. Người ta làm một lối đi xung quanh vườn (thuộc đất của vườn) rộng 2m, diện tích còn lại là 4524m². Tính các kích thước của vườn.

Xem đáp án

Gọi x, y lần lượt là chiều rộng và chiều dài của mảnh đất.

Điều kiện: $\{\begin{matrix} x > 0 \\ y > 0 \end{matrix}$ .

Vì chu vi của khu vườn là 280m nên ta có phương trình:

$2 x + 2 y = 280 \Leftrightarrow x + y = 140$ (1)

Người ta làm một lối đi xung quanh vườn (thuộc đất của vườn) rộng 2m. Nên chiều rộng và chiều dài còn lại là: x-2 và y-2.

Diện tích mảnh đất khi đã làm lối đi là: $(x - 2) (y - 2) = 4524$ (2)

Từ (1) và (2) ta có hệ phương trình: $\{\begin{matrix} x + y = 140 \\ (x - 2) (y - 2) = 4524 \end{matrix}$

Giải hệ phương trình này và đối chiếu điều kiện của mảnh đất thấy nghiệm là: $\{\begin{matrix} x = 60 \\ y = 80 \end{matrix}$ .

Vậy chiều rộng của mảnh đất là 60m và chiều dài của mảnh đất là 80m.

Câu 2:

Một hình chữ nhật có chu vi 90m. Nếu tăng chiều rộng lên gấp đôi và giảm chiều dài đi 15m thì ta được hình chữ nhật mới có diện tích bằng diện tích hình chữ nhật ban đầu. Tính các cạnh của hình chữ nhật đã cho.

Xem đáp án

Gọi x, y lần lượt là chiều rộng và chiều dài của mảnh đất.

Điều kiện: $\{\begin{matrix} x > 0 \\ y > 0 \end{matrix}$ .

Hình chữ nhật có chu vi 90m nên có phương trình:

$2 x + 2 y = 90 \Leftrightarrow x + y = 45$ (1)

Diện tích hình chữ nhật ban đầu và giảm chiều dài đi 15m thì ta được hình chữ nhật mới có diện tích bằng diện tích ban đầu.

Diện tích hình chữ nhật lúc sau là: $2 x (2 y - 15)$

Theo giả thiết thì: $2 x (y - 15) = x y$ (2)

Từ (1) và (2) thì ta có hệ phương trình: $\{\begin{matrix} x + y = 45 \\ 2 x (y - 15) = x y \end{matrix}$

Giải hệ phương trình này và sau đó đối chiếu điều kiện ta được nghiệm của hệ phương trình là: $\{\begin{matrix} x = 15 \\ y = 30 \end{matrix}$ .

Vậy hình chữ nhật có chiều rộng là 15m và chiều dài hình chữ nhật là 30m.

Câu 3:

Một thửa ruộng hình tam giác có diện tích 180m². Tính chiều dài cạnh đáy thửa ruộng, biết rằng nếu tăng cạnh đáy thêm 4m và chiều cao giảm đi 1m thì diện tích không đổi.

Xem đáp án

Gọi x (m) là cạnh đáy hình tam giác của thửa ruộng.

y (m) là chiều cao của hình tam giác của thửa ruộng.

Điều kiện: $\{\begin{matrix} x > 0 \\ y > 0 \end{matrix}$ .

Diện tích thửa ruộng lúc chưa tăng là: $S = \frac{1}{2} x y (m^{2})$ .

Theo bài toán ta có: $\frac{1}{2} x y = 180 \Leftrightarrow x y = 360$ (1)

Nếu tăng cạnh đáy thêm 4m và chiều cao giảm đi 1m thì ta có diện tích của thửa ruộng lúc này là:

$S = \frac{1}{2} (x + 4) (y - 1) (m^{2})$

Do diện tích không đổi nên:

$\frac{1}{2} (x + 4) (y - 1) = 180 \Leftrightarrow (x + 4) (y - 1) = 360$ (2)

Từ (1) và (2) ta có hệ phương trình: $\{\begin{matrix} x y = 360 \\ (x + 4) (y - 1) = 360 \end{matrix}$

Giải hệ phương trình này và đối chiếu với điều kiện ta có nghiệm của hệ phương trình là: $\{\begin{matrix} x = 36 \\ y = 10 \end{matrix}$ .

Vậy cạnh đáy của thửa ruộng ban đầu là 36m và chiều cao cạnh đáy của thửa ruộng ban đầu: 10m.

Câu 4:

Một thửa ruộng hình chữ nhật. Nếu tăng chiều dài thêm 2m và chiều rộng 3m thì diện tích tăng 100m². Nếu cùng giảm chiều dài và chiều rộng 2m thì diện tích giảm 68m². Tính diện tích thửa ruộng đó.

Xem đáp án

Gọi x, y lần lượt là chiều rộng và chiều dài của thửa ruộng.

Điều kiện: $\{\begin{matrix} x > 0 \\ y > 0 \end{matrix}$ .

Diện tích thửa ruộng là $x y (m^{2})$ .

Nếu tăng chiều dài thêm 2m và chiều rộng 3m thì diện tích tăng 100m² nên ta có phương trình:

$(x + 3) (y + 2) = x y + 100$ (1)

Nếu cùng giảm chiều dài và chiều rộng 2m thì diện tích giảm 68m² nên ta có phương trình:

$(x - 2) (y - 2) = x y - 68$ (2)

Từ (1) và (2) ta có hệ phương trình: $\{\begin{matrix} (x + 3) (y + 2) = x y + 100 \\ (x - 2) (y - 2) = x y - 68 \end{matrix}$ .

Giải hệ phương trình này và đối chiếu điều kiện ta được $\{\begin{matrix} x = 14 \\ y = 22 \end{matrix}$ thoả mãn.

Vậy thửa ruộng có chiều rộng là 14m và chiều dài là 22m.

Câu 5:

Nếu giảm chiều dài 20m và tăng chiều rộng lên 20m của một hình chữ nhật thì diện tích của nó tăng 400m². Biết rằng chu vi của hình chữ nhật này bằng 200m. Tính diện tích hình chữ nhật.

Xem đáp án

Gọi $x (m)$ và $y (m)$ lần lượt là chiều dài và chiều rộng của hình chữ nhật. Điều kiện: x, y > 0.

Chu vi hình chữ nhật bằng 200m nên

$2 (x + y) = 200 \Leftrightarrow x + y = 100 \Leftrightarrow y = 100 - x$ .

Diện tích hình chữ nhật là xy.

Nếu giảm chiều dài 20m và tăng chiều rộng 20m của hình chữ nhật thì diện tích của nó tăng 400m² nên ta có:

$(x - 20) (y + 20) = x y + 400$

$\Leftrightarrow x y + 20 x - 20 y - 400 = x y + 400$

$\Leftrightarrow 20 x - 20 y = 800 \Leftrightarrow x - y = 40$

Mà $y = 100 - x$ nên

$x - (100 - x) = 40 \Leftrightarrow 2 x = 140 \Leftrightarrow x = 70 \Rightarrow y = 30$

Diện tích hình chữ nhật: $x y = 70.30 = 2100 (m^{2})$ .

Câu 6:

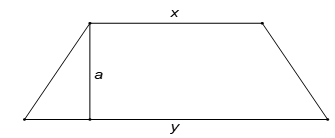
Một miếng đất hình thang cân có đáy nhỏ kém đáy lớn là 3m, và chiều cao của hình thang cân là 8m. Nếu gấp đôi đáy nhỏ và thêm đáy lớn 1m (giữ nguyên chiều cao) thì diện tích đám đất đó tăng thêm 36m² so với diện tích ban đầu. Tính số đo đáy lớn, đáy nhỏ và cạnh bên của mảnh đất đó.

Xem đáp án

Gọi $x (m)$ là đáy bé của hình thang cân,

$y (m)$ là đáy lớn của hình thang cân.

Điều kiện: x, y > 0.

Hình thang cân có đáy nhỏ kém đáy lớn là 3m nên ta có phương trình:

$y = x + 3 \Leftrightarrow x - y = - 3$

Khi đó diện tích của hình thang cân là:

$S = \frac{1}{2} (x + y) .8 = 4. (x + y) = 4 x + 4 y$

Khi gấp đôi đáy nhỏ và thêm đáy lớn 1m (giữ nguyên chiều cao) thì diện tích của miếng đất hình thang cân mới là:

$S = \frac{1}{2} (2 x + y + 1) .8 = 4 (2 x + y + 1) = 8 x + 4 y + 4$

Theo giả thiết thì diện tích đám đất có tăng thêm 36m² so với diện tích ban đầu nên ta có phương trình:

$8 x + 4 y + 4 - (4 x + 4 y) = 36$

$\Leftrightarrow 8 x + 4 y + 4 - 4 x - 4 y = 36$

$\Leftrightarrow 4 x = 32 \Leftrightarrow x = 8$

Vậy đáy nhỏ của miếng đất hình thang cân là 8m và đáy lớn của miếng đất hình thang cân là 11m.

Áp dụng công thức Pythagore (hình vẽ), ta được độ dài cạnh bên của miếng đất hình thang cân là: $\sqrt{8^{2} + {1,5}^{2}} \approx 8,14 (m)$ .