9 câu hỏi trắc nghiệm thuộc Chủ đề 7: Đối xứng trục và các bài toán thực tiễn

Câu 1:

Có hai điểm dân cư cùng phía bên cạnh một dòng sông. Người ta muốn xây dựng một trạm cung cấp nước lấy từ dòng sông và qua xử lí cung cấp cho hai điểm dân cư nói trên. Vậy phải đặt trạm xử lí nước tại điểm nào trên bờ sông để độ dài đường ống dẫn nước từ đó tới hai điểm dân cư là nhỏ nhất?

Xem đáp án

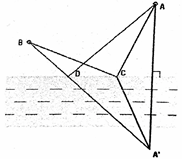
Có hai điểm dân cư cùng phía bên cạnh một dòng sông. Người ta muốn xây dựng một trạm (ảnh 1)

Trong thực tế đường ngắn nhất giữa hai điểm dân cư là đường thẳng nối hai điểm đó. Nhưng bài toán ra là đường ống nối hai điểm dân cư với một điểm xử lí nước trên bờ sông. Vậy đường ống phải là đường gấp khúc. Giả sử hai điểm dân cư ở hai phía khác nhau của bờ sông thì bài toán trở nên quá dễ, vì đường nối hai điểm có cắt dòng sông và điểm cắt đó chính là trạm xử lí nước. Bài toán của chúng ta là hai điểm dân cư cùng một phía bờ sông, nên chúng ta giả sử một điểm dân cư được chuyển sang bên kia bờ sông. Câu hỏi được đặt ra là điểm dân cư được chuyển sang bên kia sông ở vị trí nào là thích hợp nhất? Để đảm bảo tính chất của điểm dân cư ta chuyển sang phải có khoảng cách từ đó đến dòng sông là như nhau. Hay nói cách khác ta lấy điểm đối xứng của một điểm dân cư. Gọi A, B là hai điểm dân cư. Điểm A' đối xứng với B qua dòng sông. Đường nối A'B cắt bờ sông ở D. Điểm D chính là nơi đặt trạm xử lí nước.

Thật vậy với mọi điểm C khác D, ta có:

$C A + C B = C A^{'} + C B > A^{'} B = D A^{'} + D B = D A + D B$

Câu 2:

Đường quốc lộ và đường ống dân dầu cắt nhau một góc nhỏ hơn 45⁰, trong góc này có một bãi đỗ các ô tô của xí nghiệp vận tải. Xây trạm cung cấp xăng ở vị trí nào trên đường ống để các loại xe xuất phát từ bãi đỗ xe đến lấy xăng rồi ra đường quốc lộ với đường đi ngắn nhất.

Xem đáp án

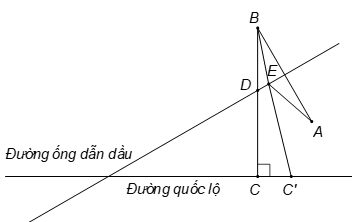
Đường quốc lộ và đường ống dân dầu cắt nhau một góc nhỏ hơn 45 độ, trong góc này có một (ảnh 1)

Ta thấy điểm dân cư A và điểm lối thoát ra đường quốc lộ nằm cùng một phía đường ống dẫn đầu. Tương tự như ví dụ 1, ta lấy điểm B đối xứng với điểm A qua đường ống dẫn dầu.

Từ điểm B hạ đường vuông góc xuống đường quốc lộ, đường ta vừa hạ sẽ cắt đường ống dẫn dầu tại D, có chân đường vuông góc tại C. Điểm D chính là nơi ta xây trạm cung cấp xăng và đoạn đường $A D + D C$ là đoạn đường ngắn nhất ta phải mở.

Thật vậy, gọi E là điểm bất kì trên đường ống dẫn dầu, C' là điểm bất kì trên đường quốc lộ. Ta có:

$A E + E C^{'} = B E + E C^{'} \geq B C^{'} \geq B C = B D + D C = A D + D C$

(do BC là đoạn đường ngắn nhất từ B đến đường quốc lộ).

Câu 3:

Một mảnh đất hình tam giác nhọn ABC nằm ở vị trí giao nhau của ba con sông. Trong mảnh đất này có hai nhà máy D và E. Tàu chở hàng thả hàng ở ba vị trí $M, K, L$ lần lượt nằm trên các cạnh $A C, A B, B C$ của tam giác ABC. Hãy tìm các vị trí bỏ hàng $M, K, L$ để quãng đường đi từ D đến M, đến K đến L rồi đến E là nhỏ nhất.

Xem đáp án

Gọi D₁ và E₁ lần lượt đối xứng với D và E qua AC và BC.

Gọi D₂ đối xứng với D₁ qua AB. Nối $D_{2} E_{1}$ và dựng đường gấp khúc $D M^{'} K^{'} L^{'} E$ (hình vẽ).

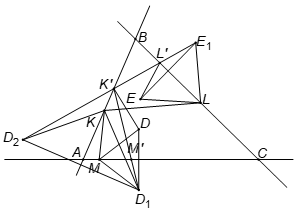
Một mảnh đất hình tam giác nhọn ABC nằm ở vị trí giao nhau của ba con sông. Trong mảnh (ảnh 1)

Ta thấy rằng mọi đường gấp khúc $D M K L E$ đều lớn hơn đường gấp khúc $D M^{'} K^{'} L^{'} E$ .

Thật vậy

$D M^{'} + M^{'} K^{'} + K^{'} L^{'} + L^{'} E = D_{1} M^{'} + M^{'} K^{'} + K^{'} L^{'} + L^{'} E = D_{2} K^{'} + K^{'} L^{'} + L^{'} E_{1} = D_{2} E_{1} \leq D_{2} K + K L$

$+ L E_{1} = D_{1} K + K L + L E \leq D_{1} M + M K + K L + L E = D M + M K + K L + L E$ .

Hay kết quả ta có: $D M^{'} + M^{'} K^{'} + K^{'} L^{'} + L^{'} E \leq D M + M K + K L + L E$ (đpcm).

Câu 4:

Trong lòng một con sông rộng có một hòn đảo hình tròn. Người ta muốn xây dựng những bến đỗ cho các tàu chở khách du lịch để chở khách từ đảo lên một bờ rồi nhận khách, đi sang ngay bờ bên kia nhận khách tiếp rồi chở về đảo hoặc ngược lại. Phải đặt các bến ở đâu để đường đi trên sông là ngắn nhất, biết rằng đường thẳng hai bờ sông kéo dài cắt nhau tại O tạo thành một góc nhọn.

Xem đáp án

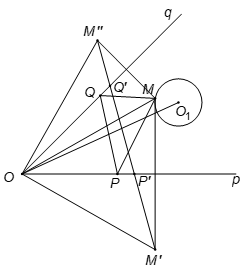
Trong lòng một con sông rộng có một hòn đảo hình tròn. Người ta muốn xây dựng những bến (ảnh 1)

Đặt hình tròn là hòn đảo trong góc nhọn Opq giới hạn bởi hai bờ sông. Bài toán đưa ra đi tìm tam giác MPQ sao cho M thuộc đường tròn, P thuộc Op và Q thuộc Oq sao cho chu vi tam giác MPQ nhỏ nhất.

Ta có định điểm bất kì M trên đường tròn và lấy M' và M'' là các điểm đối xứng với M qua Op và Oq. Tìm điểm P thuộc
Op và điểm Q thuộc Oq sao cho chu vi tam giác MPQ có chu vi nhỏ nhất. Từ ví dụ 1, ta có kết quả điểm P' và Q' là những giao điểm của M'M'' với Op và Oq tương ứng.

Trong trường hợp này chu vi tam giác MPQ trùng với M'M''. Nhưng M'M'' là cạnh đáy của tam giác cân $M^{'} M^{''} O$ với một góc cố định ở đỉnh. Suy ra M'M'' sẽ nhỏ nhất khi M phải là giao điểm của đường tròn với đoạn thẳng OO₁, ở đây O₁ là tâm đường tròn.

Câu 5:

Có hai kho chứa xăng hình tròn ở cùng một phía đối với đường quốc lộ. Người ta muốn xây dựng một trạm cung ứng và phân phối xăng bên đường quốc lộ nối với hai đường ống nối tới hai bồn xăng là ngắn nhất.

Xem đáp án

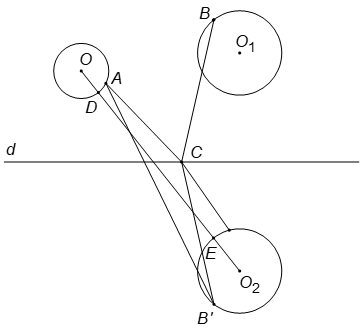
Gọi $(O_{2})$ , B' lần lượt là hình tròn và điểm đối xứng với $(O_{1})$ , B qua d (d biểu trưng cho đường

quốc lộ).

Nối $C A, C B, C B^{'}$ .

Ta có $C A + C B = C A + C B^{'}$ .

Do $C A + C B^{'} \geq A B^{'} \geq D E$ (D, E lần lượt là giao điểm của đoạn $O O_{2}$ với các đường tròn $(O), (O_{2})$ ).

Hãy các điểm D và E là các điểm cần tìm. Từ đây suy ra các điểm A, B và C cần tìm. Đó là, điểm A trùng với điểm D, điểm C là giao điểm của DE với d và điểm B'' là điểm đối xứng với điểm E qua d.

Câu 6:

Trên một mảnh đất hình thang vuông ABCD người ta xây dựng một sân vận động hình chữ nhật AEFD và 3 ngôi nhà. Nhà bảo vệ C, nhà ban quản lý sân B, nhà tạm nghỉ và thay trang phục P. Kèm theo đó người ta xây dựng hai cửa chính Q, H và cùng một cửa phụ K. Bạn hãy giúp người thiết kế sân tìm vị trí P, Q, H, K sao cho trước và sau mỗi trận thi đấu, người bảo vệ có thể đi theo con đường $C \to H \to K \to Q \to B \to P \to C$ ngắn nhất để làm nhiệm vụ. Theo đó người ta cho xây các cửa $P, H, Q, K$ và con đường BPC. Sơ đồ mảnh đất và vị trí cố định của B, C và các vị trí cần được xác định $P, Q, H, K$ có dạng như hình vẽ.

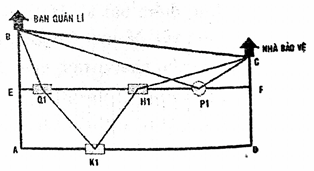
Trên một mảnh đất hình thang vuông ABCD người ta xây dựng một sân vận động hình chữ nhật (ảnh 1)

Xem đáp án

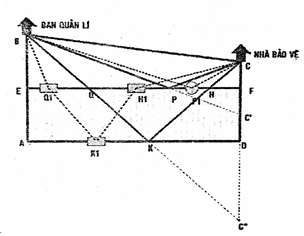
Trên một mảnh đất hình thang vuông ABCD người ta xây dựng một sân vận động hình chữ nhật (ảnh 2)

Ta giải bài toán này như sau: Con đường $C \to H \to K \to Q \to B \to P \to C$ , sẽ ngắn nhất nếu ta tìm được $P, Q, H, K$ mà $S_{1} = P B + P C$ nhỏ nhất và $S_{2} = C H + H K + K Q + Q B$ nhỏ nhất.

Ta xác định các vị trí $P, Q, H, K$ như sau:

- Gọi C' là điểm đối xứng với C qua EF; gọi C'' là điểm đối xứng với C qua AD.

- Gọi B là giao điểm của BC' và EF; K là giao điểm của BC'' và EF; H là giao điểm của CK và EF.

Việc chứng minh điểm P dựng như trên để S₁ nhỏ nhất đã trình bày trong ví dụ 1. Việc dựng điểm K như trên, cũng như theo ví dụ 1 đã nêu thì mới đảm bảo cho $S = B K + K C$ nhỏ nhất.

Ta sẽ chứng minh các điểm $K, Q, H$ dựng như vậy thoả mãn $S_{2} = C H + H K + K Q + Q B$ nhỏ nhất.

Thật vậy: xét các điểm $K_{1}, Q_{1}, H_{1}$ bất kỳ lần lượt thuộc $A D, E F$ . Ta nhận thấy:

$\{\begin{matrix} C H_{1} + H_{1} K_{1} \geq C K_{1} \\ K_{1} Q_{1} + Q_{1} B \geq K_{1} B \end{matrix} \Rightarrow C H_{1} + H_{1} K_{1} + K_{1} Q_{1} + Q_{1} B \geq C K_{1} + K_{1} B$

Theo cách dựng điểm K thì $C K_{1} + K_{1} B \geq K B + K C$

Từ đó suy ra: $C H_{1} + H_{1} K_{1} + K_{1} Q_{1} + Q_{1} B \geq K B + K C$

Dấu “=” trong $C H_{1} + H_{1} K_{1} + K_{1} Q_{1} + Q_{1} B \geq K B + K C$
xảy ra khi và chỉ khi các dấu “=” trong

$C H_{1} + H_{1} K_{1} \geq C K_{1}, K_{1} Q_{1} + Q_{1} B \geq K_{1} B, C H_{1} + H_{1} K_{1} + K_{1} Q_{1} + Q_{1} B \geq C K_{1} + K_{1} B,$

$C K_{1} + K_{1} B \geq K B + K C$ đồng thời xảy ra. Như vậy $K, Q, H$ dựng như hình trên đảm bảo cho ta S₂ là nhỏ nhất.

Tóm lại: $S_{1} + S_{2} = C H + H K + K Q + Q B + B P + P C$ , với cách dựng $P, Q, H, K$ như trên thì $S_{1} + S_{2}$ nhỏ nhất. Do các điểm P, K là duy nhất, nên vị trí các điểm P, Q, H, K như trên là duy nhất. Để ý là mảnh đất ABCD là hình thang vuông, sân vận động AEFD là hình chữ nhật nên ta chứng minh được các vị trí P, Q, H, K xác định như trên là thoả mãn các yêu cầu thực tế của bài toán. (Cụ thể là: $Q, P, H$ nằm trên cạnh EF; K nằm trên cạnh AD của hình chữ nhật ABCD và P nằm giữa Q và H).

Câu 7:

Cho hình vuông ABCD. Hãy xác định đường thẳng đi qua tam hình vuông cắt các cạnh đối AD và BC sao cho tổng khoảng cách từ bốn đỉnh của hình vuông đến đường thẳng đó là

a) Lớn nhất

Xem đáp án

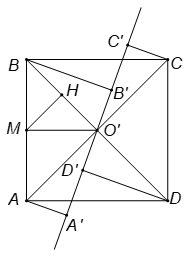
Cho hình vuông ABCD. Hãy xác định đường thẳng đi qua tam hình vuông cắt các cạnh đối AD và (ảnh 1)

Gọi d là đường thẳng qua tâm O' của hình vuông, m là tổng các khoảng cách từ bốn đỉnh của hình vuông đến d.

Xét trường hợp đường thẳng d cắt hai cạnh đối AD và BC. Kẻ $A A^{'}, B B^{'}, C C^{'}, D D^{'}$ vuông góc với d.

Ta thấy $m = A A^{'} + B B^{'} + C C^{'} + D D^{'} = 2 (A A^{'} + B B^{'})$ .

Gọi M là trung điểm của AB, N là trung điểm của A'B'. Ta có $M N ⊥ A^{'} B^{'}$ và MN là đường trung bình của hình thang ABB'A' nên $A A^{'} + B B^{'} = 2 M N$ .

Do đó: m lớn nhất $\Leftrightarrow M N$ lớn nhất.

m nhỏ nhất $\Leftrightarrow M N$ nhỏ nhất.

a) Ta có $M N \leq M O^{'}$ (không đổi) nên MN lớn nhất.

$\Leftrightarrow N \equiv O^{'} \Leftrightarrow d ∥ A B$ .

Câu 8:

b) Nhỏ nhất.

Xem đáp án

b) Kẻ $M H ⊥ O^{'} B$ , thì ta sẽ chứng minh được $M N \geq M H$ (không đổi) nên MN nhỏ nhất $M N \geq M H$ hay d trùng với BD (hoặc AC).

Tóm lại:

- Nếu d đi qua điểm O' và song song với một trong các cạnh của hình vuông thì tổng khoảng cách từ các đỉnh của hình vuông tới d là lớn nhất.

- Nếu d trùng với một trong các đường chéo của hình vuông thì tổng khoảng cách từ các đỉnh của hình vuông tới d là nhỏ nhất.

Câu 9:

Cho tam giác nhọn ABC. Hãy nội tiếp trong tam giác ABC một tam giác có chu vi bé nhất.

Xem đáp án

Cho tam giác nhọn ABC. Hãy nội tiếp trong tam giác ABC một tam giác có chu vi bé nhất. (ảnh 1)

Xét những tam giác nội tiếp PMN có đỉnh P cố định trên đáy BC.

Lấy $P_{1}, P_{2}$ đối xứng của P qua AB và AC, $P_{1}, P_{2}$ cắt AB, AC tại N và M. PMN là tam giác cần dựng vì chu vi tam giác PMN bằng $P N + N M + M P = P_{1} P_{2} < P_{1} N^{'} + N^{'} M^{'} + M^{'} P_{2}$ bằng
chu vi tam giác PM'N.

Như vậy, chúng ta cần phải tìm vị trí P để $P_{1} P_{2}$ là bé nhất.

Do $P_{1} P_{2}$ là đáy tam giác cân $A P_{1} P_{2}$ có $\hat{P_{1} A P_{2}} = 2 \hat{B A C}$ không đổi. Suy ra $P_{1} P_{2}$ đạt giá trị nhỏ nhất khi cạnh bên $A P_{1} = A P_{2} = A P$ bé nhất khi $A P ⊥ B C$ . Hay AP là đường cao của tam giác ABC.

Tương tự lập luận trên lấy điểm N thuộc AB cố định hay M thuộc AC cố định ta đi đến kết luận chu vi tam giác ABC bé nhất khi CN và BM là các đường cao của tam giác ABC.