Đề thi Học kì 1 Toán 9 có đáp án năm 2022-2023 (Đề 9)
-
4640 lượt thi
-
10 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 2:
b) 4x4 – 5x2 – 9 = 0
Xem đáp án
b) 4x4 – 5x2 – 9 = 0
Đặt ẩn số phụ , điều kiện
Lập được phương trình trung gian
Giải đúng phương trình trung gian
Tìm đúng tập nghiệm
Câu 3:
Cho hàm số y = 2x2 .
a) Vẽ đồ thị (P) của hàm số trên .
Xem đáp án
a) Vẽ đồ thị (P) của hàm số y = 2x2 .
Lập đúng bảng giá trị
Vẽ đúng các điểm theo bảng giá trị
Vẽ đồ thị chính xác
Câu 4:
b) Chứng tỏ rằng , trên cùng một mặt phẳng tọa độ Oxy , (P) và đường thẳng (d): y = 2013x -2014 có hai giao điểm nằm ở bên phải trục tung
Xem đáp án
b) Chứng tỏ được (P) và (d): y = 2013x -2014 có hai giao điểm
Phương trình hoành độ giao điểm x2 – 2013x + 2014 = 0 có > 0
x1.x2 > 0 => hai giao điểm nằm cùng một phía đối với trục tung
x1 + x2 > 0 => hai giao điểm nằm cùng phía phải đối với trục tung
Câu 5:
Cho phương trình bậc hai có ẩn x : x2 – 2mx + 2m – 1 = 0
a) Lập biệt thức ', suy ra phương trình luôn luôn có nghiệm với mọi m.
Xem đáp án
a) Lập đúng biệt thức '
Rút gọn ' = ( m – 1 )2
Câu 6:
b) Với giá trị nào của m, thì phương trình có hai nghiệm phân biệt x1,x2 thỏa mãn: x12 + x22 = 2 .
Xem đáp án
b) Tính đúng tổng và tích theo m
Tính đúng x12 + x22 theo m : x12 + x22 = 4m2 – 4m +2
x12 + x22 = 2 4m2 – 4m = 0
Tính được m = 0 ; m = 1
Chỉ chọn m = 0
Câu 7:
Một chiếc ô che nắng hình nón có vành là một đường tròn đường kính 1,6m và chiều cao 0,6m.Tính diện tích vải để làm ô.
Xem đáp án
Ta có bán kính R = 0,8 m
Diện tích cần tìm là
Câu 8:
Cho tam giác nhọn ABC nội tiếp đường tròn tâm O, đường cao BH và CK lần lượt cắt đường tròn tại E và F.
a) Chứng minh tứ giác BKHC nội tiếp. Xem đáp án
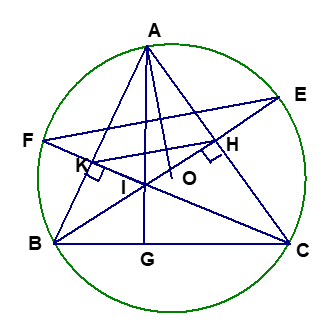
a) Do nên tứ giác
BKHC nội tiếp được đường tròn
Câu 9:
b) Chứng minh: và EF // HK.
Xem đáp án
b) Từ câu a) suy ra (cùng chắn cung KH) Do đó
Ta có
Mặt khác: , do đó
Vậy EF // HK
Câu 10:
c) Gọi I là giao điểm của BH và CK. Chứng minh rằng bán kính đường tròn ngoại tiếp tam giác AIB bằng bán kính đường tròn ngoại tiếp tam giác BIC.
Xem đáp án
c) Gọi G là giao điểm của AI và BC , hai tam giác vuông ABG và CBK có góc B chung nên . Vậy A và C thuộc hai cung chứa góc dựng trên đoạn BI, tức là tam giác AIB và tam giác BIC nội tiếp hai đường tròn có cùng bán kính.