9 câu hỏi trắc nghiệm thuộc Đề thi Học kì 1 Toán 9 có đáp án năm 2022-2023 (Đề 29) - vietjack.online

Đề thi Học kì 1 Toán 9 có đáp án năm 2022-2023

Đề số 1
Đề số 2
Đề số 3
Đề số 4
Đề số 5
Đề số 6
Đề số 7
Đề số 8
Đề số 9
Đề số 10
Đề số 11
Đề số 12
Đề số 13
Đề số 14
Đề số 15
Đề số 16
Đề số 17
Đề số 18
Đề số 19
Đề số 20
Đề số 21
Đề số 22
Đề số 23
Đề số 24
Đề số 25
Đề số 26
Đề số 27
Đề số 28
Đề số 29
Đề số 30

Đề thi Học kì 1 Toán 9 có đáp án năm 2022-2023 (Đề 29)

4559 lượt thi
9 câu hỏi
45 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

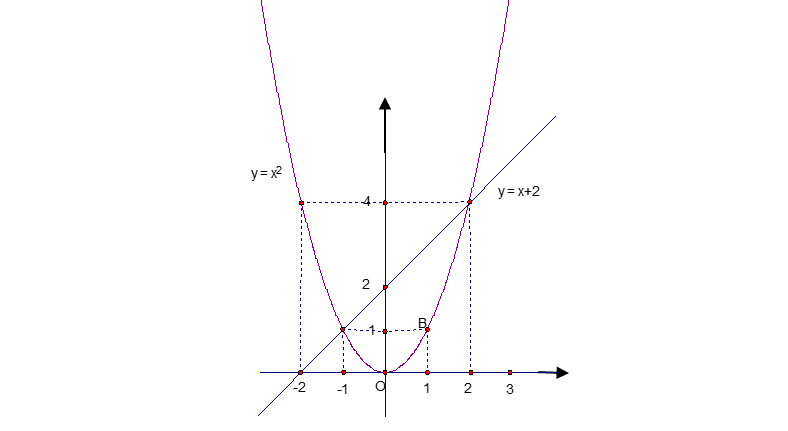
Cho hai hàm số y = x² (1) và y = x + 2 (2)

a) Vẽ đồ thị hai hàm số (1) và (2) trên cùng một mặt phẳng tọa độ

a) Cho chính xác các điểm đặc biệt, vẽ chính xác đồ thị

Cho hai hàm số y = x2 (1) và y = x + 2 (2) a) Vẽ đồ thị hai hàm số (1) và (2) trên cùng một mặt phẳng tọa độ (ảnh 1)

Câu 2:

b) Xác định tọa độ giao điểm của hai hàm số trên.

b) Lập phương trình hoành độ giao điểm của y = x² (1) và y = x + 2 (2) là:

x² = x + 2 <=> x² - x – 2 = 0 (*)

Giải phương trình (*), ta được x = -1 và x = 2

+ Với x = -1 suy ra y = 1

+ Với x = 2 suy ra y = 4

Vậy, hai hàm số y = x² (1) và y = x + 2 (2) có hai giao điểm là ( -1; 1) ; (2; 4).

Câu 3:

Giải hệ phương trình sau bằng phương pháp thế :

\{\begin{cases} x - y = 3 \\ 2 x + 3 y = 1 \end{cases}

$\{\begin{cases} x - y = 3 \\ 2 x + 3 y = 1 \end{cases} \Leftrightarrow \{\begin{cases} x = y + 3 \\ 2 (y + 3) + 3 y = 1 \end{cases} \Leftrightarrow \{\begin{cases} x = y + 3 \\ 5 y = - 5 \end{cases} \Leftrightarrow \{\begin{cases} x = 2 \\ y = - 1 \end{cases}$

Vậy, hệ phương trình có một nghiệm duy nhất là (2; -1)

Câu 4:

Cho phương trình (ẩn x) $x^{2} - 2 (m - 1) x + m^{2} = 0$

△'

a) $Δ' = {(m - 1)}^{2} - 1. m^{2} = - 2 m + 1$

Câu 5:

b) Với giá trị nào của m thì phương trình trên có nghiệm ?

b) Để phương trình có nghiệm thì

Δ' \geq 0

hay

- 2 m + 1 \geq 0 \Rightarrow m \leq \frac{1}{2}

Câu 6:

Cho tứ giác ABCD nội tiếp nửa đường tròn đường kính AD. Hai đường chéo AC và BD cắt nhau tại E. Kẻ EF vuông góc với AD. Gọi M là trung điểm của DE. Chứng minh rằng:

a) Tia CA là tia phân giác của góc BCF

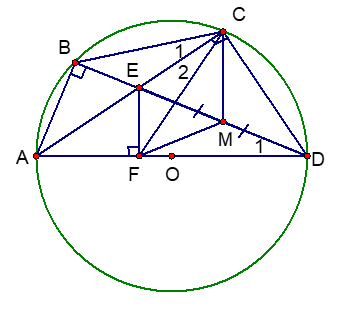
Cho tứ giác ABCD nội tiếp nửa đường tròn đường kính AD. Hai đường chéo AC và BD cắt nhau tại E. Kẻ EF vuông góc với AD. Gọi M là trung điểm của DE. Chứng minh rằng: a) Tia CA là tia phân giác của góc BCF (ảnh 1)

a) Ta chứng minh tứ giác ECDF nội tiếp được

(Vì $\hat{E C D} = \hat{EFD} = 90^{0}$ )

Suy ra $\hat{C_{2}} = \hat{D_{1}}$ (góc nội tiếp cùng chắn cung EF) (1)

Suy ra $\hat{C_{1}} = \hat{D_{1}}$ (góc nội tiếp cùng chắn cung AB) (2)

Từ (1) và (2) suy ra $\hat{C_{1}} = \hat{C_{2}}$

Do đó CA là tia phân giác của góc BCF

Câu 7:

b) Tứ giác BCMF nội tiếp được.

b) Ta có MF = MD ( MF là trung tuyến ứng với cạnh huyền của tam giác vuông), suy ra $Δ M F D$ cân ở M và $\hat{M B F} = 2 \hat{D_{1}}$

Ta lại có

\hat{B C F} = 2 \hat{D_{1}}

( từ câu a). Do đó

\hat{B M F} = \hat{B C F}

suy ra tứ giác BCMF nội tiếp được.

Câu 8:

Cho một hình trụ có bán kính đáy r = 5cm và chiều cao h = 10cm

a) Tính diện tích xung quanh của hình trụ

a) Diện tích xung quanh của hình trụ:

S_{x q} = 2 π r h = 2 π .5.10 = 100 π (c m^{2})

Câu 9:

b) Tính thể tích của hình trụ ?

b) Thể tích của hình trụ:

V = π r^{2} h = π 5^{2} .10 = 250 π (c m^{3})

Bắt đầu thi ngay

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương