Đề thi Học kì 1 Toán 9 có đáp án năm 2022-2023 (Đề 11)
-
4561 lượt thi
-
10 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 3:
c)
 Xem đáp án
Xem đáp án
Câu 5:
Cho hàm số: có đồ thị là (P) và đường thẳng (D): . Tìm tọa độ giao điểm của (P) và đường thẳng (D) bằng phép toán.
 Xem đáp án
Xem đáp án
Tìm tọa độ giao điểm của (P) và đường thẳng (D) bằng phép toán.
Phương trình hoành độ giao điểm:
Vậy tọa độ giao điểm của (P) và (D) là: vàCâu 6:
Cho phương trình: (x là ẩn)
a) Chứng minh rằng phương trình trên luôn luôn có hai nghiệm phân biệt với mọi giá trị của m. Xem đáp án
Xem đáp án
a) Ta có: = (m – 3)2 – 4 .(m – 5)
= m2 – 6m + 9 – 4m + 20
= m2 – 10m + 29
= (m – 5)2 + 4 > 0 (m)
Vậy phương trình luôn luôn có hai nghiệm phân biệt với mọi giá trị của m.
Câu 7:
Cho tam giác DAB nhọn (DB < DA) nội tiếp đường tròn (O, R). Tiếp tuyến tại B và A của (O) cắt nhau tại M. MD cắt (O) tại C.
a) Chứng minh MC . MD = MA2. Xem đáp án
Xem đáp án
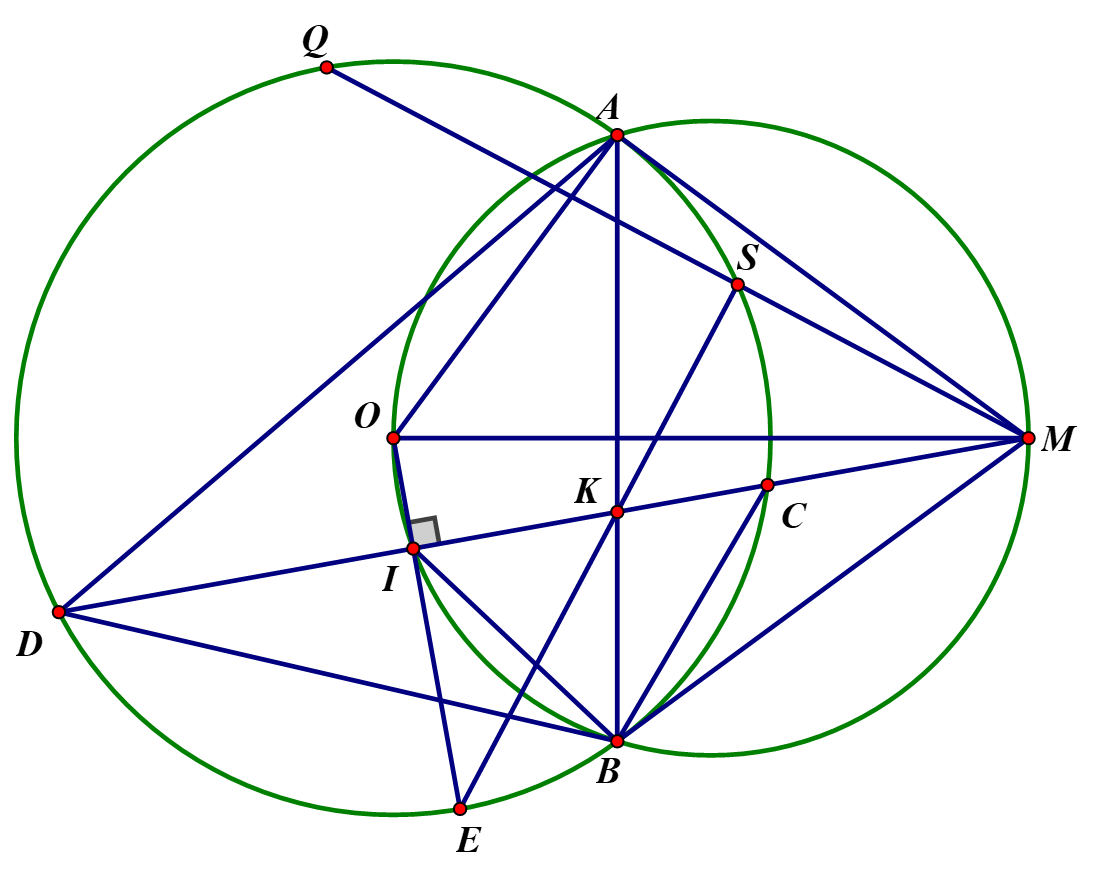
a) Chứng minh
Chứng minh MAC ~ MDA.
Chứng minh MA2 = MC . MD.Câu 8:
 Xem đáp án
Xem đáp án
b) Chứng minh AOBM nội tiếp.
Chứng minh OIDM.
Chứng minh AOIB nội tiếp.Câu 10:
 Xem đáp án
Xem đáp án
d) Chứng minh KS . KE = KI . KM (= KA . KB)
Chứng minh EISM nội tiếp.
Chứng minh E, O, Q thẳng hàng