11 câu hỏi trắc nghiệm thuộc Đề thi Học kì 1 Toán 9 có đáp án năm 2022-2023 (Đề 12) - vietjack.online

Đề thi Học kì 1 Toán 9 có đáp án năm 2022-2023

Đề số 1
Đề số 2
Đề số 3
Đề số 4
Đề số 5
Đề số 6
Đề số 7
Đề số 8
Đề số 9
Đề số 10
Đề số 11
Đề số 12
Đề số 13
Đề số 14
Đề số 15
Đề số 16
Đề số 17
Đề số 18
Đề số 19
Đề số 20
Đề số 21
Đề số 22
Đề số 23
Đề số 24
Đề số 25
Đề số 26
Đề số 27
Đề số 28
Đề số 29
Đề số 30

Đề thi Học kì 1 Toán 9 có đáp án năm 2022-2023 (Đề 12)

4137 lượt thi
11 câu hỏi
45 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Giải các phương trình và hệ phương trình:

a) 3x² – 4x +1 = 0

a) 3x² – 4x + 1 = 0

Ta có a + b + c = 0 hoặc tính được

△

= 4

x_{1} = 1; x_{2} = \frac{c}{a} = \frac{1}{3}

Câu 2:

c) $\{\begin{cases} 3 x + 2 y = 3 \\ 5 x + 3 y = 10 \end{cases}$

c) $\{\begin{cases} 3 x + 2 y = 3 \\ 5 x + 3 y = 10 \end{cases} \Leftrightarrow \{\begin{cases} 9 x + 6 y = 9 \\ 10 x + 6 y = 20 \end{cases} \Leftrightarrow \{\begin{cases} x = 11 \\ 3 x + 2 y = 3 \end{cases} \Leftrightarrow ... \Leftrightarrow \{\begin{cases} x = 11 \\ y = - 15 \end{cases}$

Câu 3:

d) (2x – 3)² = 4x + 9

d) (2x – 3)² = 4x + 9 $\Leftrightarrow$ 4x² – 12x + 9 = 4x + 9

\Leftrightarrow ... \Leftrightarrow

4x(x – 4) = 0

\Leftrightarrow ... \Leftrightarrow

x = 0 hay x = 4

Câu 4:

Cho phương trình: x² + mx + 2m – 4 = 0 (x là ẩn số)

a) Chứng tỏ phương trình luôn có nghiệm với mọi giá trị của m.

a) Tính $△$ = …= (m – 4)² $\geq 0$

=> Phương trình luôn có nghiệm với mọi m

Câu 5:

b) Tính tổng và tích của hai nghiệm theo m.

b) Tính x₁ + x₂ = – m

x₁.x₂ = 2m – 4

Câu 6:

c) Gọi x₁; x₂ là hai nghiệm của phương trình. Định m để $x_{1}^{2} + x_{2}^{2} = 5$

c) Định m để $x_{1}^{2} + x_{2}^{2} = 5$

Ta có $x_{1}^{2} + x_{2}^{2} = 5 \Leftrightarrow {(x_{1} + x_{2})}^{2} - 2 x_{1} x_{2} = 5$

$\Leftrightarrow {(- m)}^{2} - 2 (2 m - 4) = 5 \Leftrightarrow ... \Leftrightarrow m^{2} - 4 m + 3 = 0$

Có a + b + c = 0 nên m₁ = 1 và m₂ = 3

Vậy m₁ = 1 hoặc m₂ = 3 thì

x_{1}^{2} + x_{2}^{2} = 5

Câu 7:

Từ điểm A ngoài đường tròn (O; R) vẽ hai tiếp tuyến AB, AC với đường tròn (O) (B, C là tiếp điểm) và cát tuyến ADE (AD < AE và tia AE nằm giữa hai tia AB và AO). Gọi I là trung điểm của DE.

a) Chứng minh: tứ giác ABIO nội tiếp.

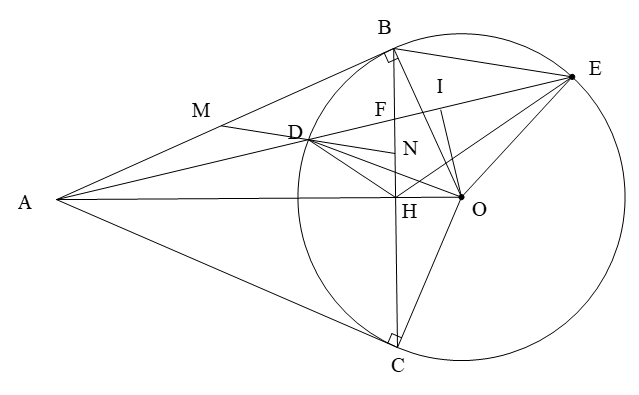
Từ điểm A ngoài đường tròn (O; R) vẽ hai tiếp tuyến AB, AC với đường tròn (O) (B, C là tiếp điểm) và cát tuyến ADE (AD < AE và tia AE nằm giữa hai tia AB và AO). (ảnh 1)

a) I là trung điểm DE $\Rightarrow O I ⊥ D E$ (Đ/k đi qua trung điểm của dây…)

Xét tứ giác ABIO có $\hat{A B O} = 90^{0}$ (AB là tiếp tuyến)

$\hat{A I O} = 90^{0}$ (OI $⊥$ DE)

\Rightarrow \hat{A B O} = \hat{A I O} = 90^{0} \Rightarrow

Tứ giác ABIO nội tiếp (2 đỉnh liên tiếp cùng nhìn…)

Câu 8:

b) Gọi H là giao điểm của AO và BC. Chứng minh: AD.AE = AH.AO.

b) AB = AC (t/c 2 tiếp tuyến cắt nhau), OB = OC (bk)

=> OA là đường trung trực của BC

Xét tam giác ABO vuông tại B có đường cao BH $\Rightarrow$ AB² = AH.AO

Xét tam giác ABD và tam giác AEB có $\hat{B A E}$ chung

$\hat{A B D} = \hat{A E B}$ (gnt và góc tạo bởi tia tt và dây cùng chắn cung BD)

=> ABD ~ AEB $\Rightarrow \frac{A B}{A E} = \frac{A D}{A B} \Rightarrow A B^{2} = A D . A E$

=> AD.AE = AH.AO (= AB²)

Câu 9:

c) Chứng minh: HB là tia phân giác của

\hat{D H E}

c) Ta có AD.AE = AH.AO

Chứng minh được tam giác ABD ~ tam giác AEB (cgc)

$\Rightarrow$ Tứ giác DHOE nội tiếp (góc ngoài bằng góc đối trong)

$\Rightarrow \hat{O H E} = \hat{O D E}$ (2 gnt cùng chắn cung OE)

OD = OE (bk) $\Rightarrow \hat{O D E} = \hat{D E O} \Rightarrow \hat{A H D} = \hat{O H E}$

$\Rightarrow \hat{D H B} = \hat{B H E}$ (2 góc phụ với 2 góc bằng nhau)

=> HB là tia phân giác của góc $\hat{D H E}$

Câu 10:

d) Qua D kẻ đường thẳng song song với BE, đường thẳng này cắt AB, BC lần lượt tại M, N. Chứng minh: MD = DN.

d) Gọi F là giao điểm của DE và BC

Ta có HF là tia phân giác góc $\hat{D H E} \Rightarrow \frac{D F}{F E} = \frac{D H}{H E}$ (t/c phân giác)

HF $⊥$ AH mà HF là phân giác trong => AH là phân giác ngoài tam giác DHE

$\Rightarrow \frac{A D}{A E} = \frac{D H}{H E} \Rightarrow \frac{D F}{F E} = \frac{A D}{A E} (= \frac{D H}{H E})$

MD // BE $\Rightarrow \frac{M D}{B E} = \frac{A D}{A E}$ (Thales), DN // BE $\Rightarrow \frac{D N}{B E} = \frac{D F}{F E}$ (Thales)

\Rightarrow \frac{M D}{B E} = \frac{D N}{B E} (do \frac{A D}{A E} = \frac{D F}{F E})

=> MD = DN

Câu 11:

Bác An gởi tiết kiệm vào ngân hàng 10 000 000 đồng (mười triệu đồng) với lãi suất 6% /năm và kỳ hạn gởi là 1 năm. Sau một năm Bác An không rút lãi do đó tiền lãi năm đầu được gộp vào với vốn để tính lãi cho năm sau và lãi suất vẫn như cũ. Hỏi sau 2 năm Bác An rút cả vốn và lãi được tất cả bao nhiêu tiền?

Sau năm thứ nhất bác An có trong ngân hàng là:

10 000 000.(1 + $\frac{5}{100}$ ) = 10 600 000 đồng

Sau 2 năm bác An lãnh cả vốn và lãi là:

10 600 000.(1 + $\frac{5}{100}$ ) = 11 236 000 đồng

Bắt đầu thi ngay

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương