9 câu hỏi trắc nghiệm thuộc Đề thi Học kì 1 Toán 9 có đáp án năm 2022-2023 (Đề 2)

Đề thi Học kì 1 Toán 9 có đáp án năm 2022-2023

Đề số 1
Đề số 2
Đề số 3
Đề số 4
Đề số 5
Đề số 6
Đề số 7
Đề số 8
Đề số 9
Đề số 10
Đề số 11
Đề số 12
Đề số 13
Đề số 14
Đề số 15
Đề số 16
Đề số 17
Đề số 18
Đề số 19
Đề số 20
Đề số 21
Đề số 22
Đề số 23
Đề số 24
Đề số 25
Đề số 26
Đề số 27
Đề số 28
Đề số 29
Đề số 30

Đề thi Học kì 1 Toán 9 có đáp án năm 2022-2023 (Đề 2)

4227 lượt thi
9 câu hỏi
45 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Không dùng máy tính, hãy giải phương trình và hệ phương trình sau:

a) $5 x^{2} - 7 x - 6 = 0$

Xem đáp án

$5 x^{2} - 7 x - 6 = 0$ . Ta có $Δ = 49 + 120 = 169 > 0.$

Vậy PT đã cho có hai nghiệm phân biệt:

x_{1} = \frac{7 + \sqrt{169}}{10} = 2, x_{2} = \frac{7 - \sqrt{169}}{10} = - \frac{3}{5}

Câu 2:

b) $\{\begin{cases} 2 x + y = 1 \\ 3 x - 2 y = 12 \end{cases}$

Xem đáp án

$\{\begin{cases} 2 x + y = 1 \\ 3 x - 2 y = 12 \end{cases} \Leftrightarrow \{\begin{cases} 4 x + 2 y = 2 \\ 3 x - 2 y = 12 \end{cases} \Leftrightarrow \{\begin{cases} 7 x = 14 \\ 3 x - 2 y = 12 \end{cases} \Leftrightarrow \{\begin{cases} x = 2 \\ 3.2 - 2 y = 12 \end{cases} \Leftrightarrow \{\begin{cases} x = 2 \\ y = - 3 \end{cases}$

Vậy hệ PT đã cho có nghiệm duy nhất (x;y) = (2;-3)

Câu 3:

Cho phương trình $x^{2} - (2 m + 1) x + m^{2} + 2$ , trong đó m là tham số.

a) Với giá trị nào của m thì phương trình trên có nghiệm?

Xem đáp án

a) Phương trình $x^{2} - (2 m + 1) x + m^{2} + 2$ có nghiệm $\Leftrightarrow Δ \geq 0$

$\Leftrightarrow$ (-(2m + 1))² – 4(m² + 2) $\geq$ 0

$\Leftrightarrow 4 m - 7 \geq 0 \Leftrightarrow 4 m \geq 7 \Leftrightarrow m \geq \frac{7}{4}$

Vậy với

m \geq \frac{7}{4}

thì PT đã cho có nghiệm

Câu 4:

b) Gọi

x_{1}, x_{2}

là hai nghiệm của phương trình trên. Tìm m để

3 x_{1} x_{2} + 7 = 5 (x_{1} + x_{2})

Xem đáp án

b) Với $m \geq \frac{7}{4}$ , PT đã cho có nghiệm. Theo hệ thức Viét, ta có:

$x_{1} + x_{2} = 2 m + 1$ và $x_{1} . x_{2} = m^{2} + 2$

Theo đề bài: $3 x_{1} x_{2} + 7 = 5 (x_{1} + x_{2}) \Leftrightarrow 3 (m^{2} + 2) + 7 = 5 (2 m + 1)$

$\Leftrightarrow 3 m^{2} - 10 m + 8 = 0 \Leftrightarrow m_{1} = 2 \geq \frac{7}{4}$ (nhận); $m_{1} = \frac{4}{7}$ (không thỏa điều kiện)

Vậy với

m_{1} = 2

thì

3 x_{1} x_{2} + 7 = 5 (x_{1} + x_{2})

Câu 5:

Giải bài toán bằng cách lập phương trình hoặc hệ phương trình.

Một tổ công nhân phải làm 144 dụng cụ. Do 3 công nhân chuyển đi làm việc khác nên mỗi người còn lại phải làm thêm 4 dụng cụ. Tính số công nhân lúc đầu của tổ nếu năng suất của mỗi người là như nhau.

Xem đáp án

Gọi x (người) là số công nhân của tổ lúc đầu. Điều kiện x nguyên và x > 3

Số dụng cụ mỗi công nhân dự định phải làm là: $\frac{144}{x}$ (dụng cụ)

Số công nhân thực tế khi làm việc là: x - 3 (người)

Do đó mỗi công nhân thực tế phải làm là: $\frac{144}{x - 3}$ (dụng cụ)

Theo đề bài ta có phương trình: $\frac{144}{x - 3} - \frac{144}{x} = 4$

Rút gọn, ta có phương trình: $x^{2} - 3 x - 108 = 0$

$Δ = 9 + 432 = 441 \Rightarrow \sqrt{441} = 21$

$x_{1} = \frac{3 + 21}{2} = 12$ (nhận); $x_{2} = \frac{3 - 21}{2} = - 9$ loại)

Vậy số công nhân lúc đầu của tổ là 12 người.

Câu 6:

Cho hình vuông ABCD, lấy một điểm M bất kỳ trên cạnh BC (M khác B và C). Qua B kẻ đường thẳng vuông góc với đường thẳng DM tại H, kéo dài BH cắt đường thẳng DC tại K.

a) Chứng minh tứ giác BHCD nội tiếp đường tròn. Xác định tâm I của đường tròn đó.

Xem đáp án

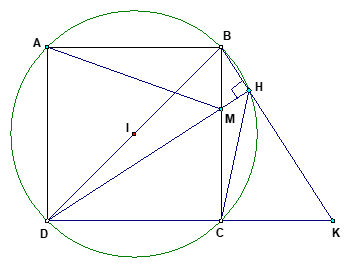
a) Ta có $\hat{B C D} = 90^{0}$ (vì ABCD là hình vuông)

$\hat{B H D} = 90^{0}$ (vì $B H ⊥ D M$ )

=> H, C cùng thuộc đường tròn đường kính BD

Vậy tứ giác BHCD nội tiếp được đường tròn đường kính BD, có tâm I là trung điểm đoạn BD.

Câu 7:

b) Chứng minh

K M ⊥ D B

Xem đáp án

b) Trong $Δ K B D$ có: $\begin{array}{l} D H ⊥ B K (g t) \\ B C ⊥ D K (g t) \end{array}\}$ (đường cao thứ ba)

Câu 8:

c) Chứng minh: KC.KD = KH.KB

Xem đáp án

c) Xét $Δ K C B$ và $Δ K H D$ có: $\overset{⏜}{C} = \overset{⏜}{H}$ = 90⁰; $\overset{⏜}{K}$ là góc chung

$\Rightarrow Δ K C B$ $Δ K H D$ (g-g)

$\Rightarrow \frac{K C}{K H} = \frac{K B}{K D}$

$\Rightarrow K C . K D = K H . K B$ (đpcm)

Câu 9:

d) Giả sử hình vuông ABCD có là a. Tính thể tích của hình do nửa hình tròn tâm I quay một vòng quanh đường kính.

Xem đáp án

d) Nửa hình tròn tâm I quay một vòng quanh đường kính, ta được một hình cầu có bán kính: $R = \frac{B D}{2}$

Trong đó: $B D = \sqrt{a^{2} + a^{2}} = a \sqrt{2} \Rightarrow R = a . \frac{\sqrt{2}}{2}$

Vậy thể tích của hình cầu là: $V = \frac{4}{3} π R^{3}$

= \frac{4}{3} . π . {(a . \frac{\sqrt{2}}{2})}^{3} = \frac{\sqrt{2}}{3} π a^{3}

(đơn vị thể tích).

Bắt đầu thi ngay