Đề thi Học kì 1 Toán 9 có đáp án năm 2022-2023 (Đề 24)
-
4565 lượt thi
-
16 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 5:
Cho đường tròn (O;R) có hai bán kính OA, OB vuông góc nhau. Diện tích hình quạt OAB là:
 Xem đáp án
Xem đáp án
Chọn C
Câu 11:
Cho phương trình bậc hai: x2 - 2(m - 1)x + m - 3 = 0. (1)
a) Chứng minh rằng phương trình (1) luôn luôn có hai nghiệm phân biệt với mọi giá trị của m. Xem đáp án
Xem đáp án
a)
Phương trình luôn có nghiệm với mọi m
Câu 12:
b) Tìm m để phương trình (1) có một nghiệm bằng 3 và tính nghiệm kia.
 Xem đáp án
Xem đáp án
b) x = 3 thay vào PT ta có 9 + 6 ( m -1) + m – 3 = 0 => m =
theo hệ thức Viet ta có x1. x2 = m – 3 => x2 = -
Câu 13:
c) Tìm m để phương trình (1) có hai nghiệm đối nhau.
 Xem đáp án
Xem đáp án
c. Vì PT có 2 nghiệm đối nhau
Câu 14:
Cho tam giác ABC có góc BAC = 600 , đường phân giác trong của góc ABC là BD và đường phân giác trong của góc ACB là CE cắt nhau tại I ( D AC và E AB )
a, CM : tứ giác AEID nội tiếp được trong đường tròn Xem đáp án
Xem đáp án
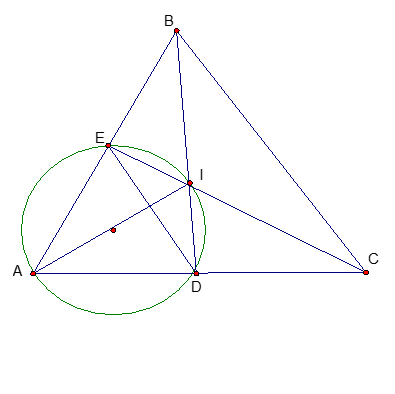
a)
mà CI , BI là phân giác => => góc BIC = 1200
mà đối đỉnh với => = 1200
xét tứ giác có => tứ giác AEID nội tiếp được trong đường trònCâu 15:
b) Chứng minh: ID = IE
 Xem đáp án
Xem đáp án
b) trong tam giác ABC có : CI , BI là phân giác => AI là phân giác => => => EI = ID
Câu 16:
c) Chứng minh: BA. BE = BD. BI
 Xem đáp án
Xem đáp án
c, xét BAI và BDE có : chung
nên BAI ~ BDE
=> => BA. BE = BD. BI