11 câu hỏi trắc nghiệm thuộc Đề thi Học kì 2 Toán 9 có đáp án năm 2022-2023 (Đề 13)

Đề thi Học kì 2 Toán 9 có đáp án năm 2022-2023

Đề số 1
Đề số 2
Đề số 3
Đề số 4
Đề số 5
Đề số 6
Đề số 7
Đề số 8
Đề số 9
Đề số 10
Đề số 11
Đề số 12
Đề số 13
Đề số 14
Đề số 15
Đề số 16
Đề số 17
Đề số 18
Đề số 19
Đề số 20
Đề số 21
Đề số 22
Đề số 23
Đề số 24
Đề số 25
Đề số 26
Đề số 27
Đề số 28
Đề số 29
Đề số 30

Đề thi Học kì 2 Toán 9 có đáp án năm 2022-2023 (Đề 13)

9383 lượt thi
11 câu hỏi
45 phút

Danh sách câu hỏi

Câu 1:

P = \frac{1}{x - 2 \sqrt{x}} - \frac{2}{x - 4}

với

x \neq 4, x > 0

a) Rút gọn biểu thức P

Xem đáp án

a) $P = \frac{1}{\sqrt{x} (\sqrt{x} - 2)} - \frac{2}{(\sqrt{x} - 2) (\sqrt{x} + 2)}$

$P = \frac{\sqrt{x} + 2}{\sqrt{x} (\sqrt{x} + 2) (\sqrt{x} - 2)} - \frac{2 \sqrt{x}}{\sqrt{x} (\sqrt{x} - 2) (\sqrt{x} + 2)}$

Thu gọn ta được $P = \frac{- 1}{\sqrt{x} (\sqrt{x} + 2)}$

Câu 2:

b) Chứng minh rằng P < 0 với mọi $x \neq 4, x > 0$

Xem đáp án

b) Với mọi $x \neq 4, x > 0$ ta có $\begin{array}{l} \sqrt{x} > 0 \\ \sqrt{x} + 2 > 0 \end{array}\} \Rightarrow \sqrt{x} (\sqrt{x} + 2) > 0$

Mà -1 < 0 nên $P = \frac{- 1}{\sqrt{x} (\sqrt{x} + 2)} < 0$ với mọi $x \neq 4, x > 0$

Câu 3:

c) Tìm những giá trị của x để $P = - \frac{1}{15}$

Xem đáp án

c) Thay $P = \frac{- 1}{\sqrt{x} (\sqrt{x} + 2)}$ vào $P = \frac{- 1}{15} \Rightarrow \frac{- 1}{\sqrt{x} (\sqrt{x} + 2)} = \frac{- 1}{15}$

Tính được x = 9 (kết hợp điều kiện thoả mãn)

Vậy x = 9 để $P = \frac{- 1}{15}$

Câu 4:

Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình

Một người đi ô tô từ A đến B cách nhau 90km. Khi đi từ B trở về A người đó tăng tốc độ 5km/h so với lúc đi, vì vậy thời gian về ít hơn thời gian đi là 15 phút. Tính tốc độ của ô tô lúc đi từ A đến B.

Xem đáp án

Gọi vận tốc của ô tô lúc đi từ A đến B là x (km/h), x > 0

Vận tốc của ô tô đi từ B trở về A là x + 5 (km/h)

Thời gian ô tô đi từ A đến B là

\frac{90}{x}

(h)

Thời gian ô tô đi từ B trở về A là

\frac{90}{x + 5}

(h)

Đổi 15 phút =

\frac{1}{4} h .

Thời gian về ít hơn thời gian đi là 15 phút nên ta được phương trình

\frac{90}{x} - \frac{90}{x + 5} = \frac{1}{4}

Giải phương trình được x = 40 (thỏa mãn điều kiện)

Vậy vận tốc của ô tô lúc đi từ A đến B là 40km/h

Câu 5:

Giải hệ phương trình

\{\begin{cases} \frac{108}{x} - \frac{63}{y} = 7 \\ \frac{81}{x} - \frac{84}{y} = 7 \end{cases}

Xem đáp án

ĐKXĐ:

x, y \neq 0

Đặt

\{\begin{cases} \frac{1}{x} = u \\ \frac{1}{y} = v \end{cases}

ta thu được hệ phương trình

\{\begin{cases} 108 u - 63 v = 7 \\ 81 u - 84 v = 4 \end{cases}

Giải hệ ta được

u = \frac{1}{27};

v = \frac{- 1}{21}

Từ đó suy ra được

x = 27; y = - 21

Câu 6:

Cho đường thẳng $(d) : y = \frac{- 1}{2} x + 2$ và Parabol $(P) : y = \frac{1}{4} x^{2}$ trên hệ trục tọa độ Oxy. Gọi A, B là hai giao điểm của (d) và (P). Tìm điểm N trên trục hoành sao cho tam giác NAB cân tại N.

Xem đáp án

Gọi A, B là hai giao điểm của (d) và (P). Tìm điểm N trên trục hoành sao cho tam giác NAB cân tại N.

Lập phương trình hoành độ giao điểm của (d) và (P) là: $\frac{1}{4} x^{2} = - \frac{1}{2} x + 2$

Giải phương trình ta được $[\begin{array}{l} x = 2 \\ x = - 4 \end{array}$

Thu được A(2;-1); B(-4;4)

Điểm N nằm trên trục hoành tọa độ N(a;0)

Tam giác NAB cân tại N nên ta có $\{\begin{cases} N A = N B \\ N \notin A B \end{cases}$

$\Leftrightarrow \{\begin{cases} \sqrt{{(a - 2)}^{2} + 1} = \sqrt{{(a + 4)}^{2} + 4^{2}} \\ - \frac{1}{2} a + 2 \neq 0 \end{cases}$

Giải được $a = - \frac{9}{4}$

Vậy tọa độ điểm

N (- \frac{9}{4}; 0)

Câu 7:

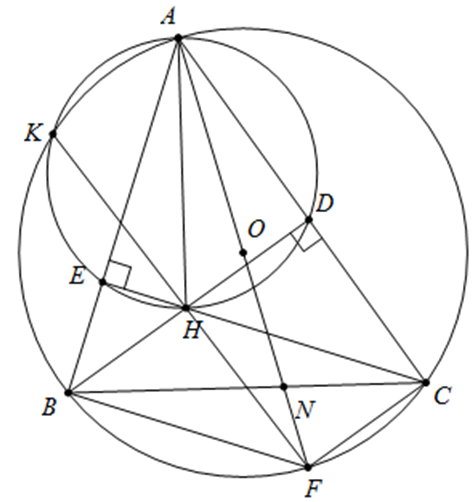
Cho đường tròn (O; R) và dây BC cố định, $B C = R \sqrt{3} .$ A là điểm di động trên cung lớn BC (A khác B, C) sao cho tam giác ABC nhọn. Các đường cao BD và CE của tam giác ABC cắt nhau tại điểm H. Kẻ đường kính AF của đường tròn (O), AF cắt BC tại điểm N.

a) Chứng minh tứ giác BEDC là tứ giác nội tiếp

Xem đáp án