Đề thi Học kì 2 Toán 9 có đáp án năm 2022-2023 (Đề 17)
-
6529 lượt thi
-
8 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 2:
Cho phương trình x2 – 2 (m + 1) x + 4m = 0 (1), (m là tham số)
a.Giải phương trình (1) với m = 2
Xem đáp án
a. Thế m = 2 vào (1) ta có phương trình : x2 – 6x + 8 = 0
x1 = 3 – 1 = 2 , x2 = 3 + = 4
Câu 3:
b. Chứng tỏ phương trình (1) luôn có nghiệm x1 , x2 mọi n
Xem đáp án
b. Chứng tỏ phương trình : (1) luôn có nghiệm mọi giá trị của m
m2 + 2m + 1 – 4m = m2 – 2m + 1
= (m – 1)2 0 với mọi m, do đó phương trình (1) luôn có nghiệm thỏa mãn với mọi m
Câu 4:
c. Tìm giá trị của m để phương trình (1) có hai nghiêm x1, x2 thỏa mãn: x1 ( 1 + x2) + x2 ( 1 + x1) = 7
Xem đáp án
c. Với x1, x2 là hai nghiệm của phương trình (1) ta có:
Theo bài ra : x1 ( 1 + x2) + x2 ( 1 + x1) = 7 x1 + x1 x2 + x2 + x1 x2= 7
x1 + x2 + 2 x1 x2= 7
2m +2 +8m= 7
10m = 5 m =
Câu 5:
Cho hàm số y = kx2, có đồ thị (P)
a. Biết điểm M ( 2,1) thuộc (P), tìm hệ số k
Xem đáp án
a. Biết điểm M ( 2,1) thuộc (P), tìm hệ số k
Vì điểm m (2;1) thuộc (P) nên ta có: 4k = 1
<=> k = = 0,25
Câu 6:
b. Với hệ số k tìm được ở câu a, tìm tọa độ giao điểm của (P) với đồ thị hàm số y = - x +3
Xem đáp án
Xét phương trình hoành độ giao điểm của đồ thị hàm số y = -x + 3 và đồ thị (P) của hàm số : y = 0,25 x2
0,25x2 = -x + 3 x2 + 4x -12 = 0Giải ra x1 = 2 x2 = -6
Với x1 = 2 => y1 = 1
x2 = 6 => y2 = 9Vậy tọa độ giao điểm của đồ thị hàm số y = -x +3 và đồ thị (P) của hàm số y = 0,25 x2 là ( 2;1) và (-6;9)
Câu 7:
b. Chứng minh tam giác AEF đồng dạng với tam giác ABC
Xem đáp án
b. Theo GT BD , CE là các đường cao của tam giác ABC nên do đó tứ giác BCDE nội tiếp
Suy ra: (1)
Mà (2) (Tổng hai góc kề)
Từ (1) và (2) suy ra
Tam giác ABC và tam giác ADE có góc A chung và góc ABC = góc ADE nên đồng dạng
Câu 8:
c. Gọi M là trung điểm của BC, chứng minh AH = 2OM
Xem đáp án
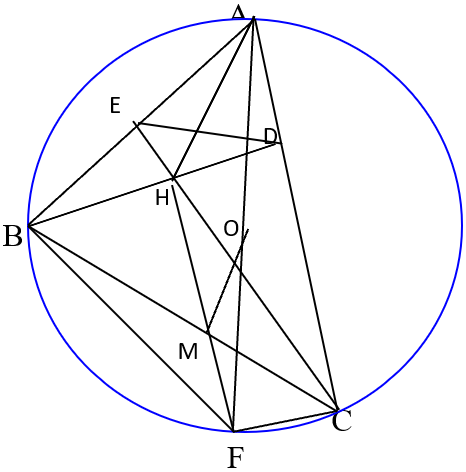
c. Vẽ đường kính AF của đường tròn tâm O ta có ACF = ABF = 90o (góc nội tiếp chắn nữa đường tròn tròn).
Suy ra BH//CF ( vì cùng vuông góc AC ) và CH // BF ( vì cùng vuông góc với AB ) Do đó tứ giác BHCF là hình bình hành
Trong hình bình hành BHCF có M là trung điểm của đường chéo BC nên 3 điểm H, M, F thẳng hàng và M cũng là trung điểm của HF
Trong tam giác AFH có OA = OF ( bán kính) và MH = MF do đó OM là đường trung bình suy ra Om = ½ AH hay AH = 2OM