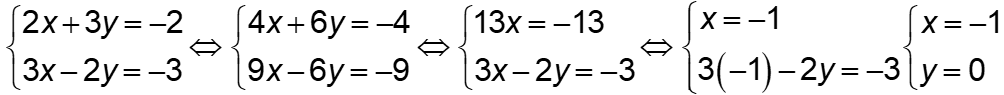15 câu hỏi trắc nghiệm thuộc Đề thi Học kì 2 Toán 9 có đáp án năm 2022-2023 (Đề 15)

Đề thi Học kì 2 Toán 9 có đáp án năm 2022-2023

Đề số 1
Đề số 2
Đề số 3
Đề số 4
Đề số 5
Đề số 6
Đề số 7
Đề số 8
Đề số 9
Đề số 10
Đề số 11
Đề số 12
Đề số 13
Đề số 14
Đề số 15
Đề số 16
Đề số 17
Đề số 18
Đề số 19
Đề số 20
Đề số 21
Đề số 22
Đề số 23
Đề số 24
Đề số 25
Đề số 26
Đề số 27
Đề số 28
Đề số 29
Đề số 30

Đề thi Học kì 2 Toán 9 có đáp án năm 2022-2023 (Đề 15)

10801 lượt thi
15 câu hỏi
45 phút

Danh sách câu hỏi

Câu 1:

\{\begin{cases} 2 x + 3 y = 5 \\ 5 x - 4 y = 1 \end{cases}

có một nghiệm là

A. (-1;1)

B. (-1;-1)

C. (1;-1)

D. (1;1)

Xem đáp án

Chọn A

Câu 2:

Trong các phương trình sau phương nào là phương trình bậc hai một ẩn:

A. (

\sqrt{3} - 1

)x²= 3x + 5

B. (m - 2)x²- 3x + 2 = 0

\frac{1}{x} = 2 x^{2} - 3

\sqrt{x^{2} + 5 x - 1} = 0

Xem đáp án

Chọn D

Câu 3:

Hàm số y = 3x²

A. Luôn đồng biến với mọi x.

B. Luôn nghịch biến với mọi x.

C. Đồng biến khi x > 0 và nghịch biến khi x < 0

D. Đồng biến khi x < 0 và nghịch biến khi x > 0

Xem đáp án

Chọn C

Câu 4:

Phương trình: x² + 3x – 4 = 0 có 2 nghiệm là

A. -1 và -4

B. 1 và - 4

C. -1 và 4.

D. 1 và 4

Xem đáp án

Chọn B

Câu 5:

Một hình trụ có diện tích xung quanh là S và thể tích là V.Nếu S và V có cùng giá trị (không kể đơn vị đo) Thì bán kính của hình trụ bằng:

A. 1

B. 2

C. 3

D. kết quả khác

Xem đáp án

Chọn B

Câu 6:

Trong hình vẽ bên TA là tiếp tuyến của đường tròn. Nếu $\overset{⏜}{A B O} = 25^{o}$ thì $\overset{⏜}{T A B}$ bằng:

Trong hình vẽ bên TA là tiếp tuyến của đường tròn. Nếu góc ABO = 25 độ thì góc TAB bằng: (ảnh 1)

A.130⁰

B. 45⁰

C. 75⁰

D. 65⁰

Xem đáp án

Chọn D

Câu 7:

Trong các khẳng định sau khẳng định nào sai .Trong một đường tròn:

A. Các góc nội tiếp bằng nhau thì các cung bị chắn bằng nhau

B. Các góc nội tiếp cùng chắn một dây thì bằng nhau

C. Với hai cung nhỏ cung nào lớn hơn thì căng dây lớn hơn

D. Góc nội tiếp không quá 90⁰bằng nửa góc ở tâm cùng chắn một cung

Xem đáp án

Chọn B

Câu 8:

Trong các khẳng định sau khẳng định nào sai .

A. Góc ở tâm của đường tròn có số đo bằng nửa số đo của cung bị chắn

B. Trong một đường tròn hai cung có số đo bằng nhau thì bằng nhau

C. Trong hai cung tròn cung nào có số đo lớn hơn thì lớn hơn

D. Số đo của nửa đường tròn bằng 180⁰

Xem đáp án

Chọn C

Câu 9:

a) Giải hệ phương trình:

\{\begin{cases} 2 x + 3 y = - 2 \\ 3 x - 2 y = - 3 \end{cases}

Xem đáp án

a) Giải hệ phương trình: 2x + 3y = -2 và 3x - 2y = -3 (ảnh 1)

Câu 10:

Cho phương trình: $x^{2} - 2 m x + 4 m - 4 = 0$ (1)

a) Giải phương trình với m = 3

Xem đáp án

a) Giải phương trình với m = 3

Với m = 3 ta có phương trình: $x^{2} - 6 x + 8 = 0$

$△' = b'^{2} - a c = 3^{2} - 8 = 1$

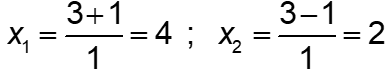
Cho phương trình: x^2 - 2mx + 4m - 4 = 0 (1) a) Giải phương trình với m = 3 (ảnh 1)

Câu 11:

b) Với giá trị nào của m thì phương trình có nghiệm

Xem đáp án

b) $△' = b'^{2} - a c = m^{2} - 4 m + 4 = {(m - 2)}^{2} \geq 0$ Với mọi số thực m

Với mọi giá trị của m thì phương trình có nghiệm.

Câu 12:

c) Viết biểu thức liên hệ giữa hai nghiệm x₁; x₂ (x₁; x₂là nghiệm của phương trình (1)) không phụ thuộc vào m.

Xem đáp án

c) Vì phương trình luôn luôn có nghiệm với mọi giá trị của m (c/m câu b)

Nên theo hệ thức Viét ta có :

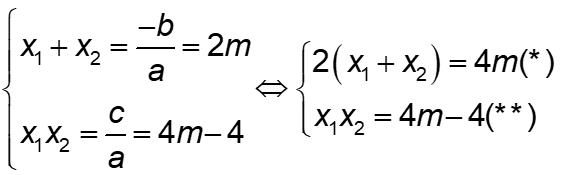
c) Viết biểu thức liên hệ giữa hai nghiệm x1; x2 (x1; x2 là nghiệm của phương trình (1)) không phụ thuộc vào m. (ảnh 1)

Trừ từng vế của phương trình (*) cho phương trình (**) ta được:

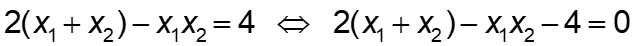
c) Viết biểu thức liên hệ giữa hai nghiệm x1; x2 (x1; x2 là nghiệm của phương trình (1)) không phụ thuộc vào m. (ảnh 2)

Đây là biểu thức liên hệ giữa hai nghiệm x₁; x₂ không phụ thuộc vào m.

Câu 13:

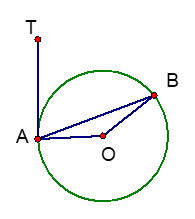
Cho tam giác nhọn ABC, các đường cao AD, BE, CF cắt nhau tại H.

a) Chứng minh 4 điểm B, E, C, F thuộc một đường tròn. Xác định tâm O của đường tròn này.

Xem đáp án

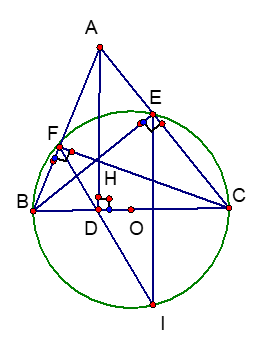
a) Chứng minh 4 điểm B,E,C,F thuộc một đường tròn.

$\overset{⏜}{B F C} = \overset{⏜}{B E C} = 90^{o}$ E, F thuộc đường tròn đường kính BC .

Tâm O của đường tròn này là trung điểm của BC.

Câu 14:

b) Chứng minh HE.HB = HD.HA = HF.HC

Xem đáp án

b) Chứng minh HE.HB = HD.HA = HF.HC

\frac{H D}{H E} = \frac{H B}{H A}

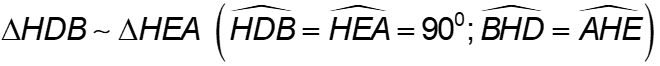=> HD.HA=HE.HB (1)

Tương tự 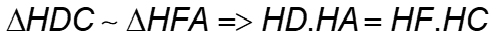(2)

Từ (1) và (2) suy ra HE.HB = HD.HA = HF.HC

Câu 15:

c) FD cắt đường tròn (O) tại I, Chứng minh EI vuông góc với BC.

Xem đáp án

c) Chứng minh EI vuông góc với BC.

* Chứng minh tứ giác BFHD nội tiếp ( $\overset{⏜}{B F H} + \overset{⏜}{B D H} = 180^{o}$ )

Suy ra: $\overset{⏜}{H F D} = \overset{⏜}{H B D}$ hai góc nội tiếp cùng chắn cung HD)

Từ đó: $\overset{⏜}{I C} = \overset{⏜}{E C}$

Vậy BC $⊥$ EI

Bắt đầu thi ngay