Bộ 30 đề thi vào 10 môn Toán có lời giải chi tiết (Đề 1)
-
5652 lượt thi
-
50 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 6:
Cho hàm số bậc nhất có đồ thị là đường số d Tìm hàm số đó biết d đi qua
 Xem đáp án
Xem đáp án
Goi hàm số cần tìm có dạng
Vì đi qua
Vậy hàm số cần tìm là
Chọn đáp án D
Câu 7:
Cho hàm số bậc nhất có đồ thị là đường thẳng d Tìm hàm số đó biết d đi qua và song song với
 Xem đáp án
Xem đáp án
Gọi là đồ thi cần tìm
Vì
Để đi qua
Vậy
Chọn đáp án B
Câu 8:
Cho hàm số bậc nhất có đồ thị là đường thẳng d Tìm hàm số đó biết d đi qua và cắt hai tia tại sao cho nhỏ nhất
 Xem đáp án
Xem đáp án
Vì d cắt tia
Dấu xảy ra khi
Vậy .Chọn đáp án C
Câu 9:
Cho hàm số bậc nhất có đồ thị là đường thẳng d Tìm hàm số đó biết d đi qua và với
 Xem đáp án
Xem đáp án
Hàm số
Đồ thị hàm số qua điểm
Vậy .Chọn đáp án A
Câu 10:
Cho đường thẳng và . Tìm tất cả các giá trị của để hai đường thẳng song song với nhau
 Xem đáp án
Xem đáp án
Để các đường thẳng và song song với nhau thì :
Chọn đáp án C
Câu 11:
Tìm phương trình đường thẳng Biết đường thẳng d đi qua điểm và tạo với hai tia một tam giác vuông cân
 Xem đáp án
Xem đáp án
Đường thẳng đi qua điểm
Ta có :
(do thuộc hai tia
Tam giác OAB vuông tại O. Do đó vuông cân khi
Vậy đường thẳng cần tìm là : .Chọn đáp án B
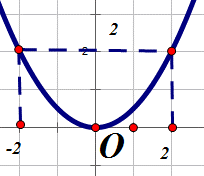
Câu 12:
Cho hàm số có đồ thị là hình dưới. Tìm a,b
 Xem đáp án
Xem đáp án
Đồ thi hàm số đi qua điểm
Chọn đáp án D
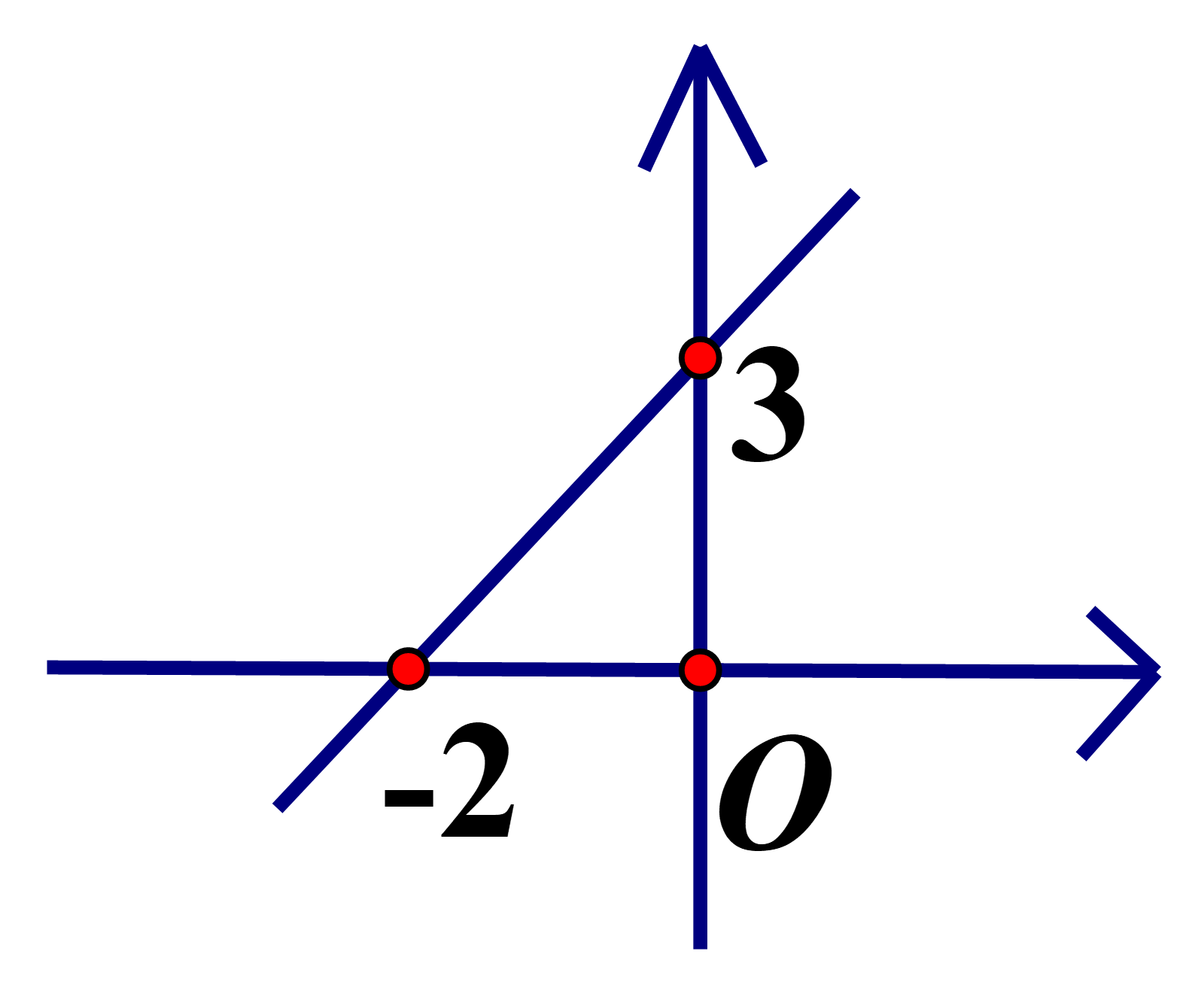
Câu 13:
 Xem đáp án
Xem đáp án
Vì đi qua và nằm về phía
Chọn đáp án D
Câu 16:
Với giá trị nào của m thì hàm số nghịch biến trên R
 Xem đáp án
Xem đáp án
hàm số nghịch biến khi
Chọn đáp án A
Câu 17:
Phương trình nào sau đây là phương trình bậc nhất hai ẩn ?
 Xem đáp án
Xem đáp án
Phương trình bậc nhất hai ẩn có dạng
Chọn đáp án D
Câu 19:
Tháng thứ nhất, hai tổ sản xuất được 1000 chi tiết máy. Tháng thứ hai tổ I vượt mức 20% và tổ II vượt mức 15% so với tháng thứ nhất. Vì vậy hai tổ sản xuất được chi tiết máy. Hỏi tháng thứ hai, mỗi tổ sản xuất được bao nhiêu chi tiết máy ?
 Xem đáp án
Xem đáp án
Gọi x,y là số chi tiết máy hai tổ tháng thứ nhất làm được
Theo bài ta có hệ phương trình :
Vậy tháng thứ hai,
Tổ I: (chi tiết máy), tổ II: (chi tiết máy)
Chọn đáp án A
Câu 20:
Cho hệ phương trình . Tìm tất cả các giá trị của để hệ phương trình trên có nghiệm duy nhất ?
 Xem đáp án
Xem đáp án
Từ thay vào (2) ta có:
Để hệ có nghiệm duy nhất thì
Chọn đáp án A
Câu 21:
Cho ba đường thẳng Miền được tạo bởi đồ thị của ba đường thẳng đã cho là tam giác gì ?
 Xem đáp án
Xem đáp án
Ta gọi là giao điểm của 2 đường thẳng đôi một của 3 dường thẳng trên
Nên vuông cân tại A. Chọn đáp án B
Câu 22:
Với những giá trị của m để phương trình có hai nghiệm phân biệt . Khi đó tính
 Xem đáp án
Xem đáp án
có nên phương trình luôn có hai nghiệm. Áp dụng hệ thức Vi – et :
Chọn đáp án D
Câu 23:
Với những giá trị của m để phương trình có hai nghiệm thỏa mãn Khi đó m là nghiệm phương trình nào dưới đây
 Xem đáp án
Xem đáp án
có nên phương trình luôn có hai ngiệm phân biệt . Ta có:
là nghiệm của phương trình
Chọn đáp án C
Câu 24:
Cho phương trình ( tham số, ẩn số). Tìm tất cả các giá trị của tham số m để phương trình có hai nghiệm phân biệt ?
 Xem đáp án
Xem đáp án
phương trình (m: tham số,x: ẩn số) là hàm số bậc hai khi
Phương trình có hai nghiệm phân biệt khi
và
Chọn đáp án B
Câu 25:
Phương trình bậc hai nào sau đây có nghiệm và
 Xem đáp án
Xem đáp án
Áp dụng hệ thức Vi et khi ta có hai nghiệm
Nên . Thấy phương trình thỏa mãn
Chọn đáp án D
Câu 30:
Một vận động viên nhảy cầu trong hồ nước. Khi nhảy, độ cao h từ người đó tới mặt nước (tính bằng mét) phụ thuộc vào khoảng cách x từ điểm rơi đến chân cầu (tính bằng mét) bởi công thức . Khi vận động viên cách mặt nước 3m tính khoảng cách x
 Xem đáp án
Xem đáp án
Khi ở độ cao 3m
Vì x là khoảng cách từ điểm rơi đến chân cầu nên
Chọn đáp án B
Câu 32:
Tìm tất cả các giá trị của tham số m để phương trình có bốn nghiệm phân biệt ?
 Xem đáp án
Xem đáp án
(1)
Đặt phương trình thành : (2)
Để phương trình (1) có 4 nghiệm phân biệt thì pt (2) có 2 nghiệm dương phân biệt
vô lý . Vậy không tìm được giá trị
Chọn đáp án D
Câu 33:
Một chiếc diều ABCD có Biết Hãy tính chiều dài cạnh và diện tích của chiếc diều (làm tròn đến hàng phần nghìn)
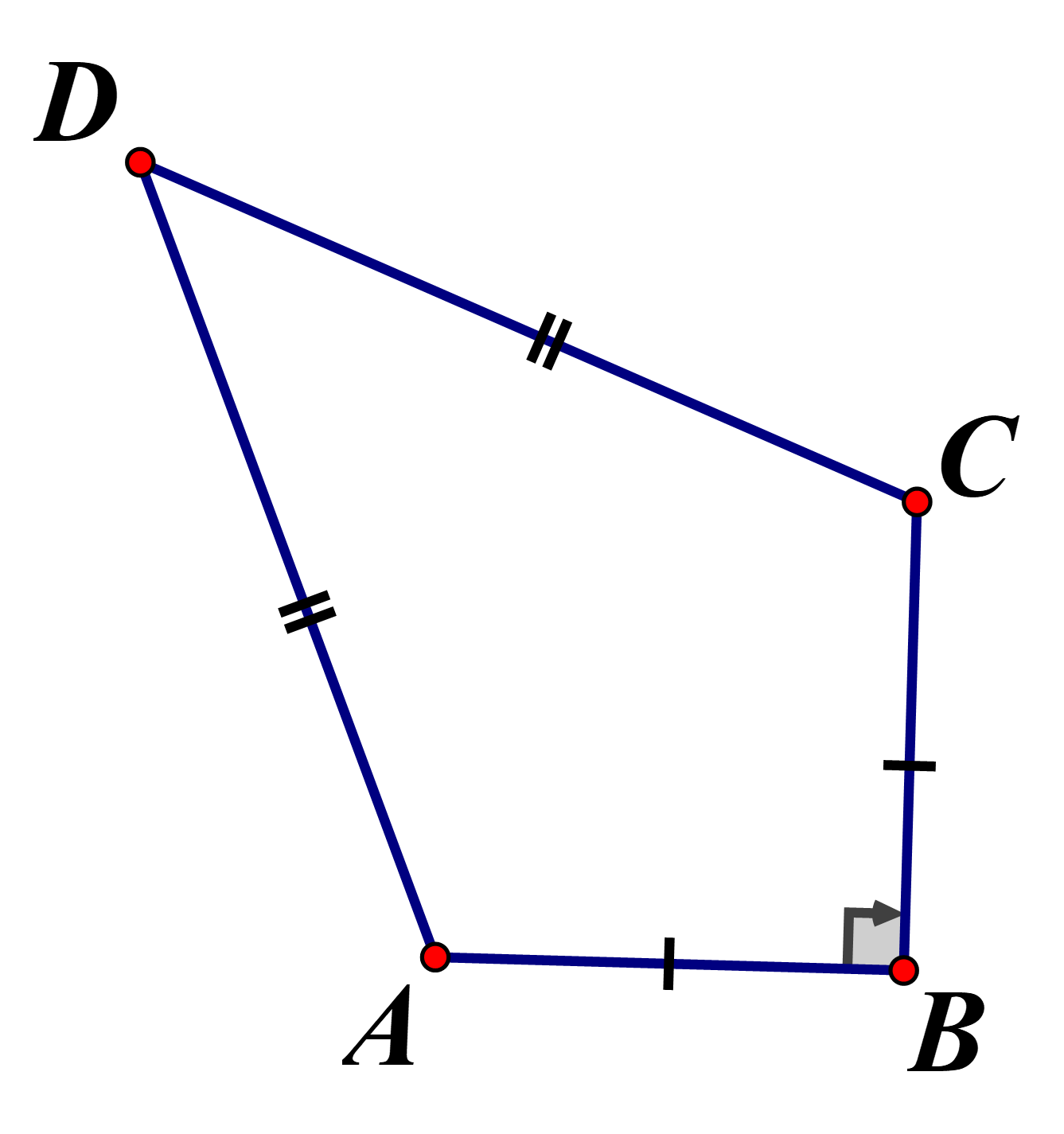
 Xem đáp án
Xem đáp án
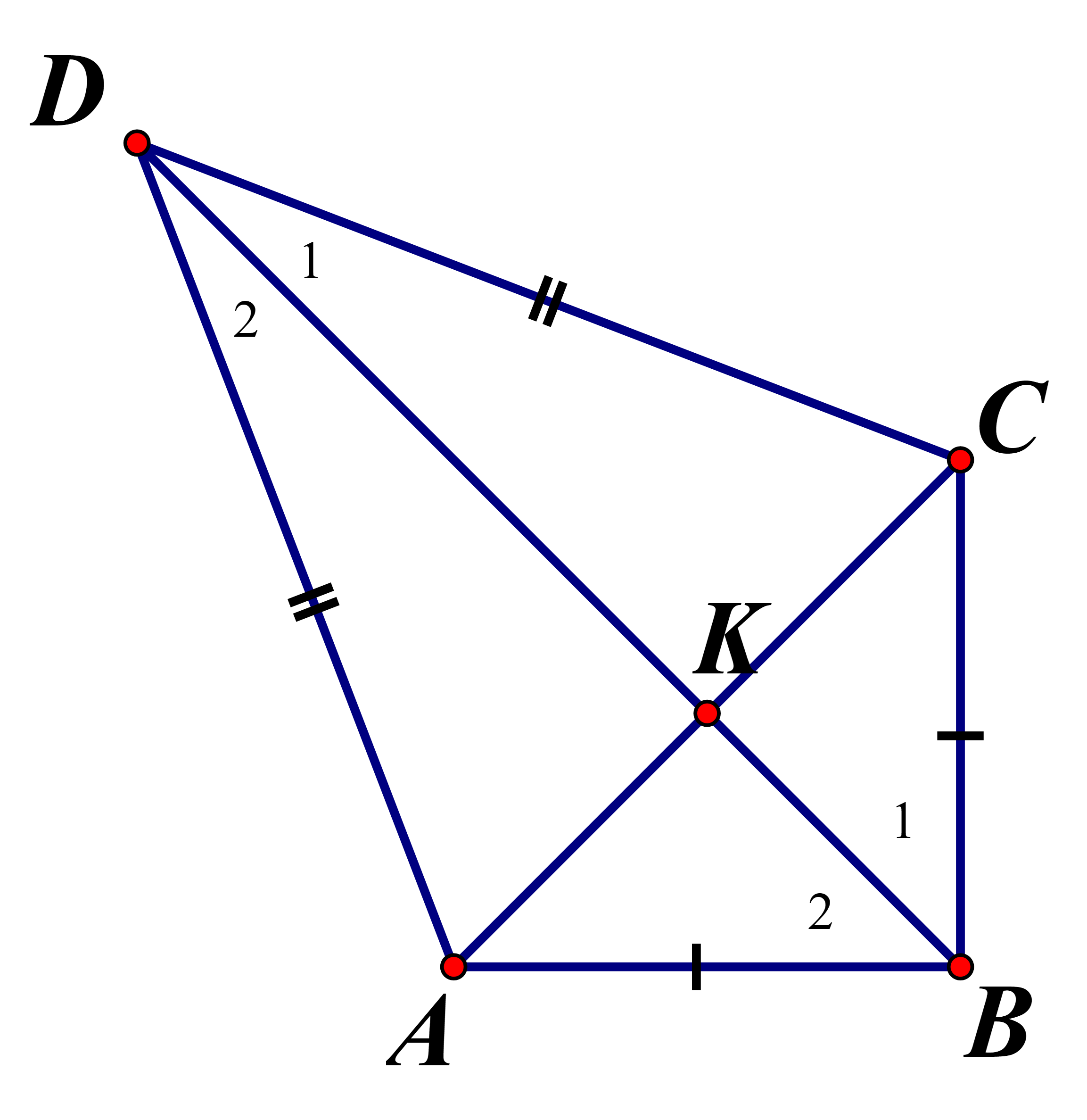
Mặt khác là đường trung trực của
Chọn đáp án C
Câu 34:
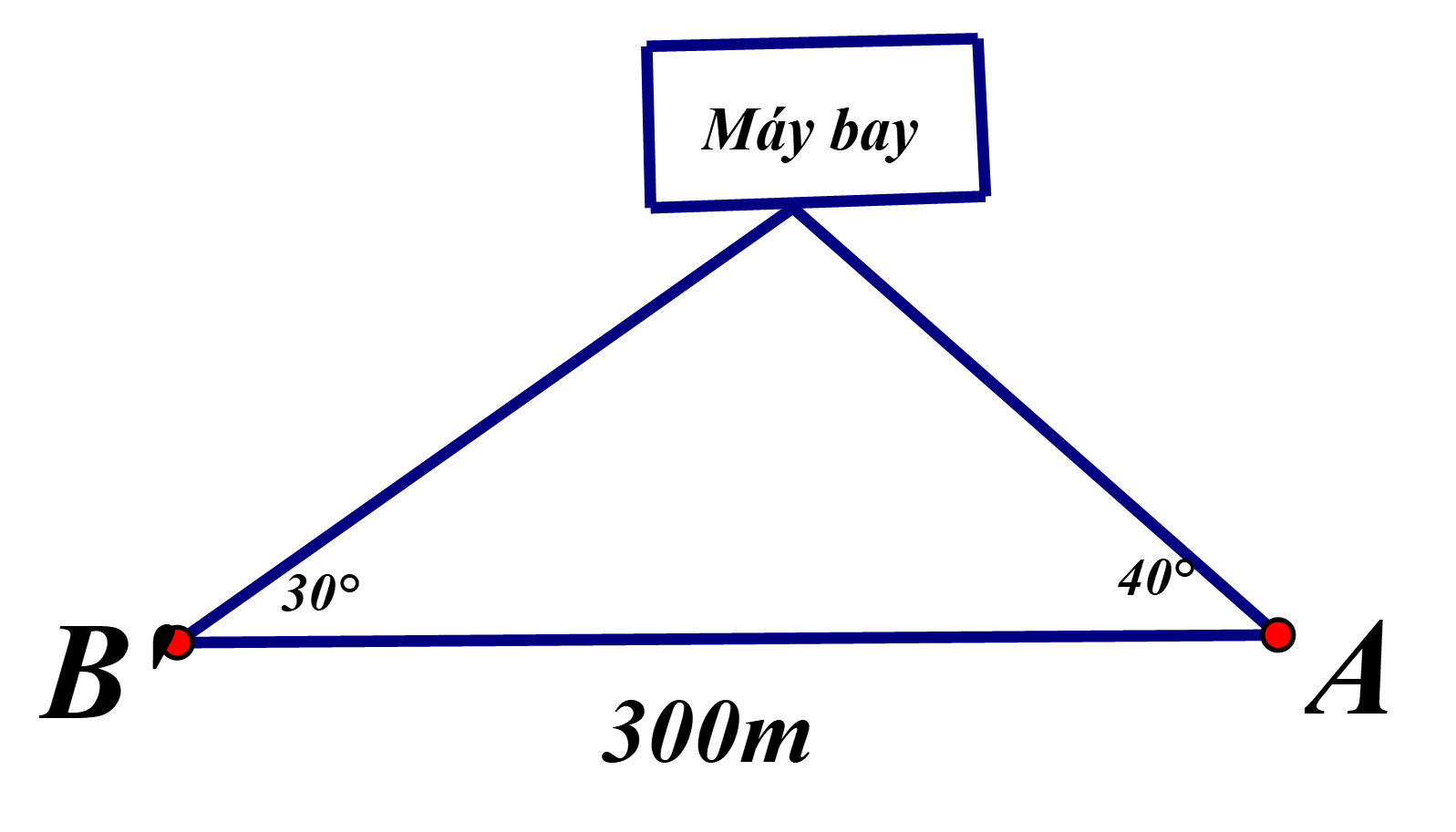
Điểm hạ cánh của một máy bay trực thăng ở giữa hai người quan sát A và B. Biết khoảng cách giữa hai người này là 300m, góc “nâng” để nhìn thấy máy bay tại vị trí A là và B tại vị trí là Hãy tính độ cao của máy bay .
 Xem đáp án
Xem đáp án
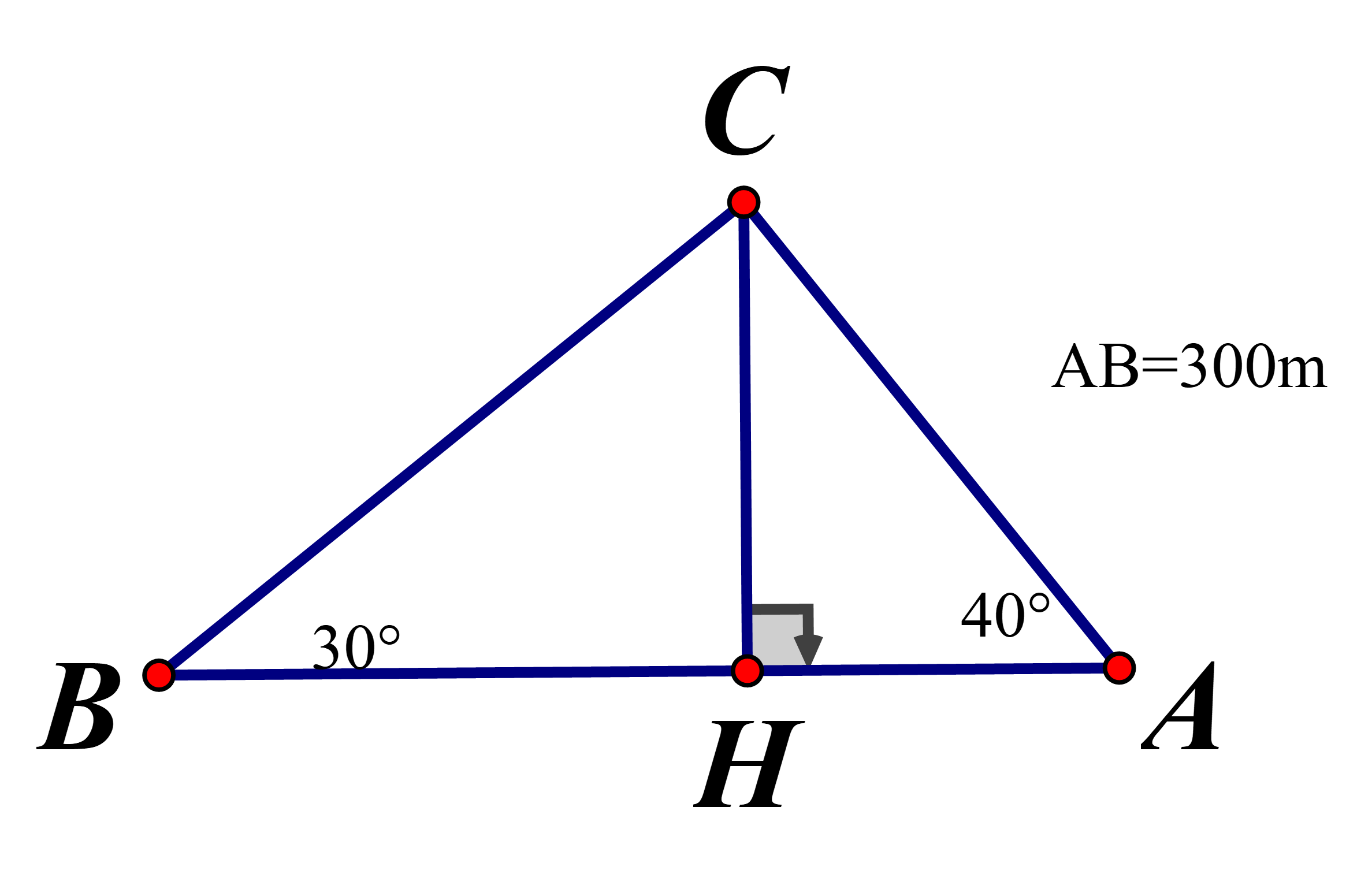
Độ cao của máy bay:CH
Xét
Xét
Chọn dáp án C
Câu 35:
Cho tam giác ABC có Góc C gần bằng góc nào nhất ?
 Xem đáp án
Xem đáp án
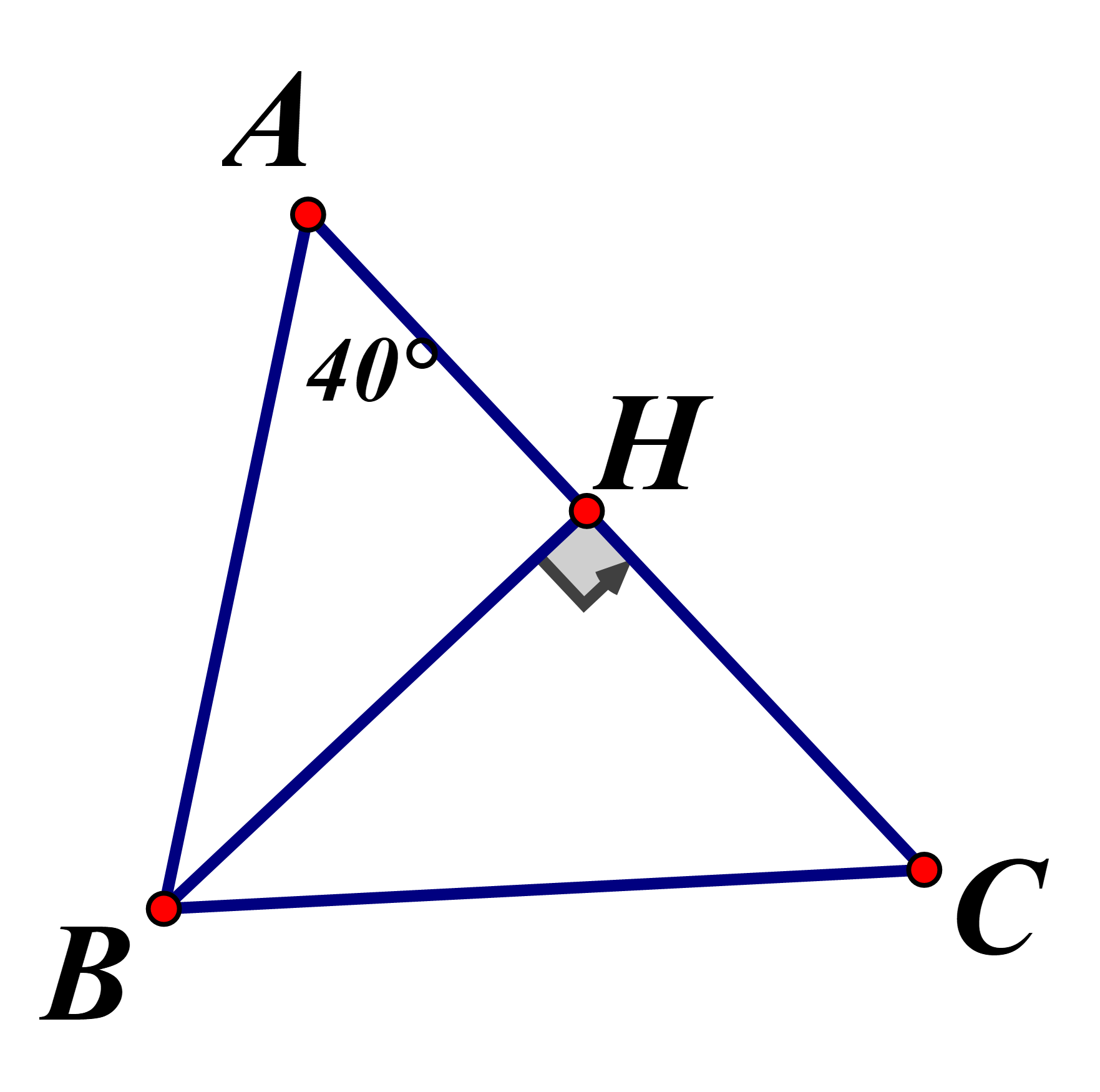
Hạ . Áp dụng tỉ số lượng giác của góc nhọn trong các tam giác vuông :
Chọn đáp án D
Câu 36:
Cho tam giác ABC có trực tâm H là trung điểm của đường cao AD Đẳng thức nào sau đây đúng ?
 Xem đáp án
Xem đáp án
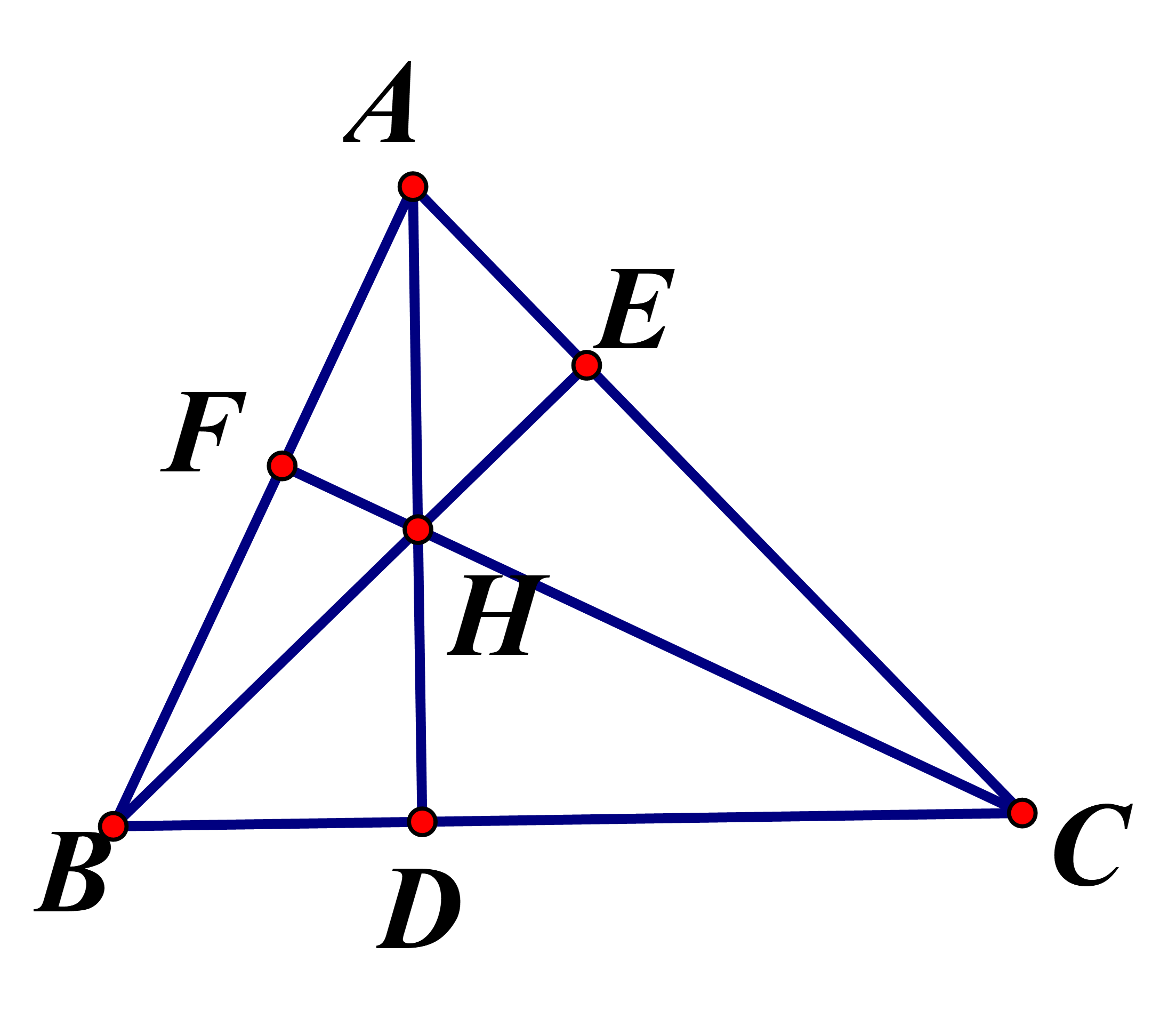
Đường cao
Chọn đáp án C
Câu 37:
Cho tam giác ABC vuông tại A Đẳng thức nào sau đây đúng ?A
 Xem đáp án
Xem đáp án
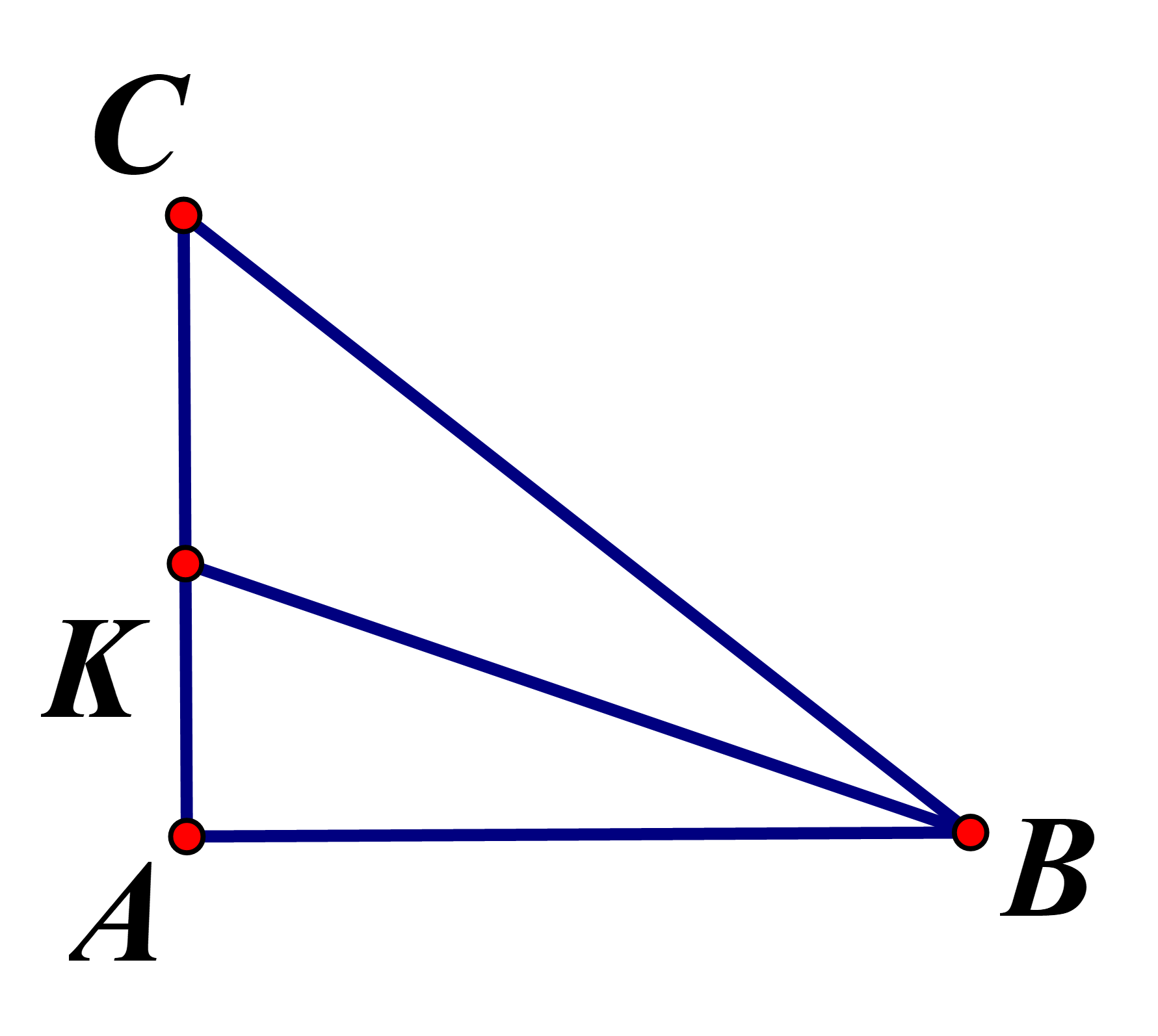
Kẻ BK là tia phân giác của . Theo tính chất tia phân giác
Áp dụng tính chất của tỉ lệ thức ta có :
Mà
Chọn đáp án C
Câu 38:
Cho một đường thẳng song song với cạnh BC cắt cạnh AB và cạnh AC lần lượt tại D và F Khẳng định nào sau đây là đúng ?
 Xem đáp án
Xem đáp án
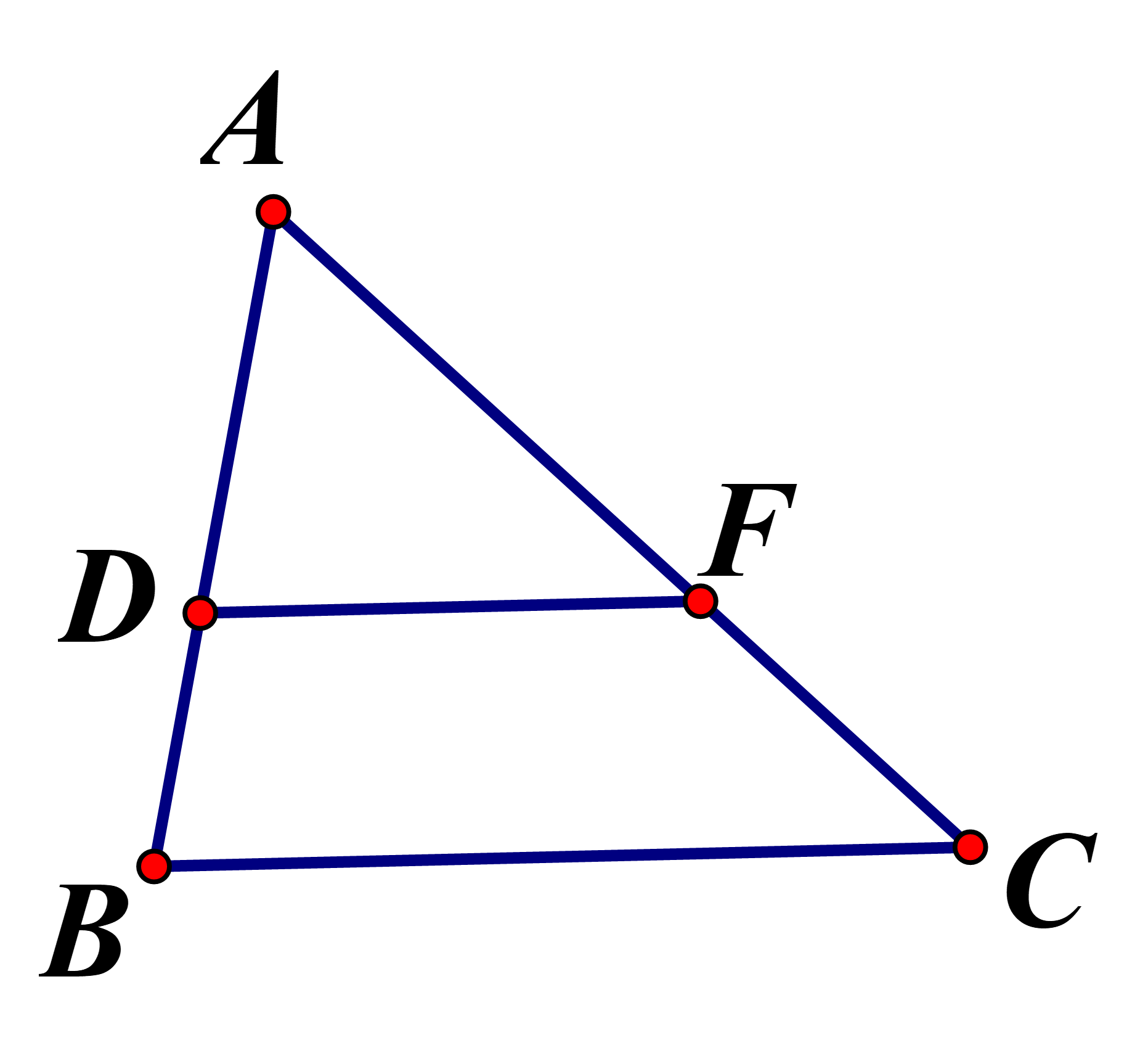
Áp dụng định lý Ta let ta có : Chọn đáp án C
Câu 39:
đồng dạng với theo tỉ số đồng dạng đồng dạng với theo tỉ số đồng dạng đồng dạng với theo tỉ số :
 Xem đáp án
Xem đáp án
đồng dạng với theo tỉ số
Chọn đáp án D
Câu 40:
Trên đường tròn lấy ba cung liên tiếp sao cho số đo của chúng đều bằng Gọi I là giao điểm của hai tia AB,DC,H là giao điểm của AC,BD hai dây Khẳng định nào sau đây sai ?
 Xem đáp án
Xem đáp án
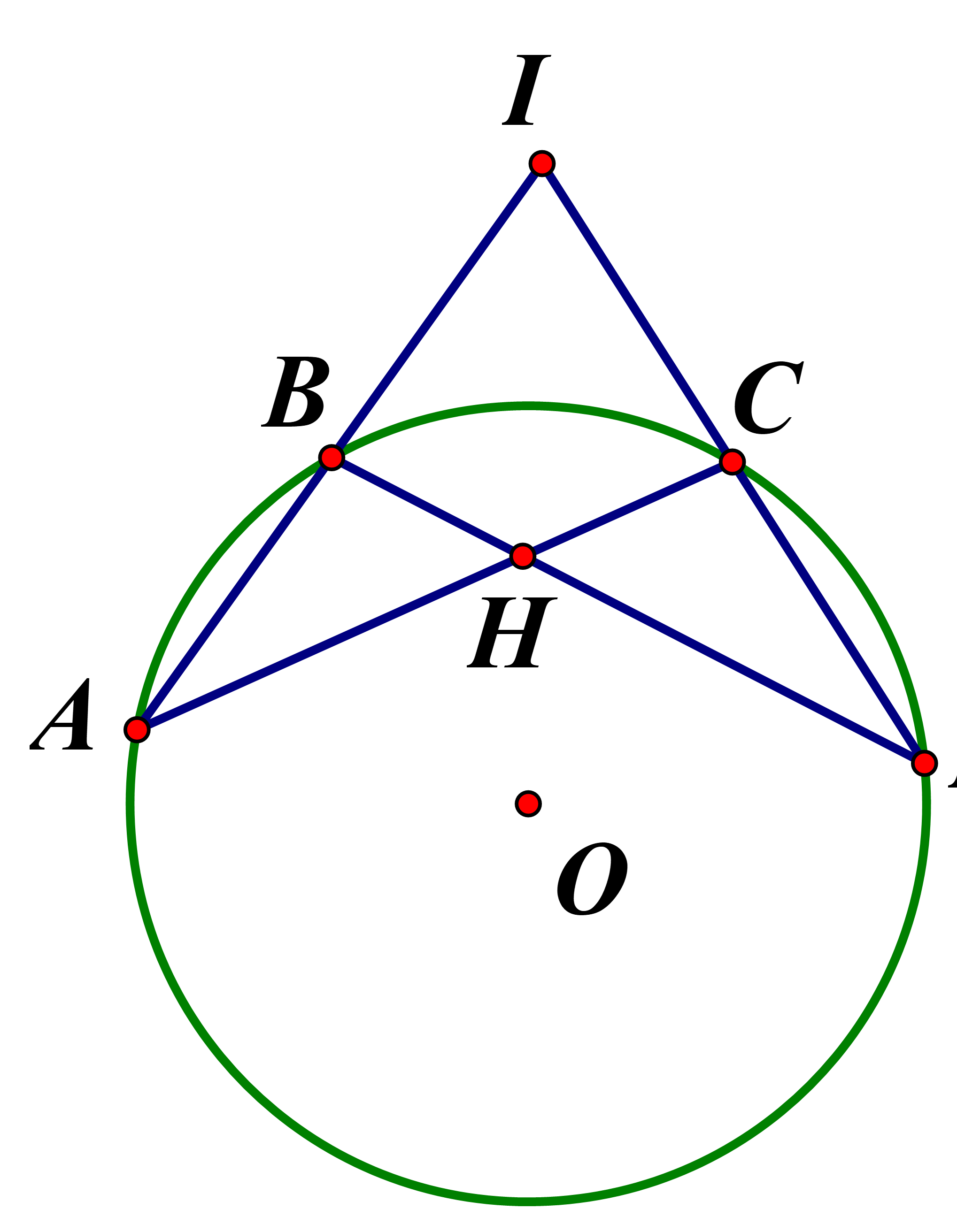
nên câu D sai
Chọn đáp án D
Câu 41:
Cho nửa đường tròn tâm O, đường kính là điểm tùy ý trên nửa đường tròn. Tiếp tuyến của tại A cắt tia BC tại D. Tia phân giác của góc cắt dây BC tại M và cung BC tại N. Tam giác là tam giác gì ?
 Xem đáp án
Xem đáp án
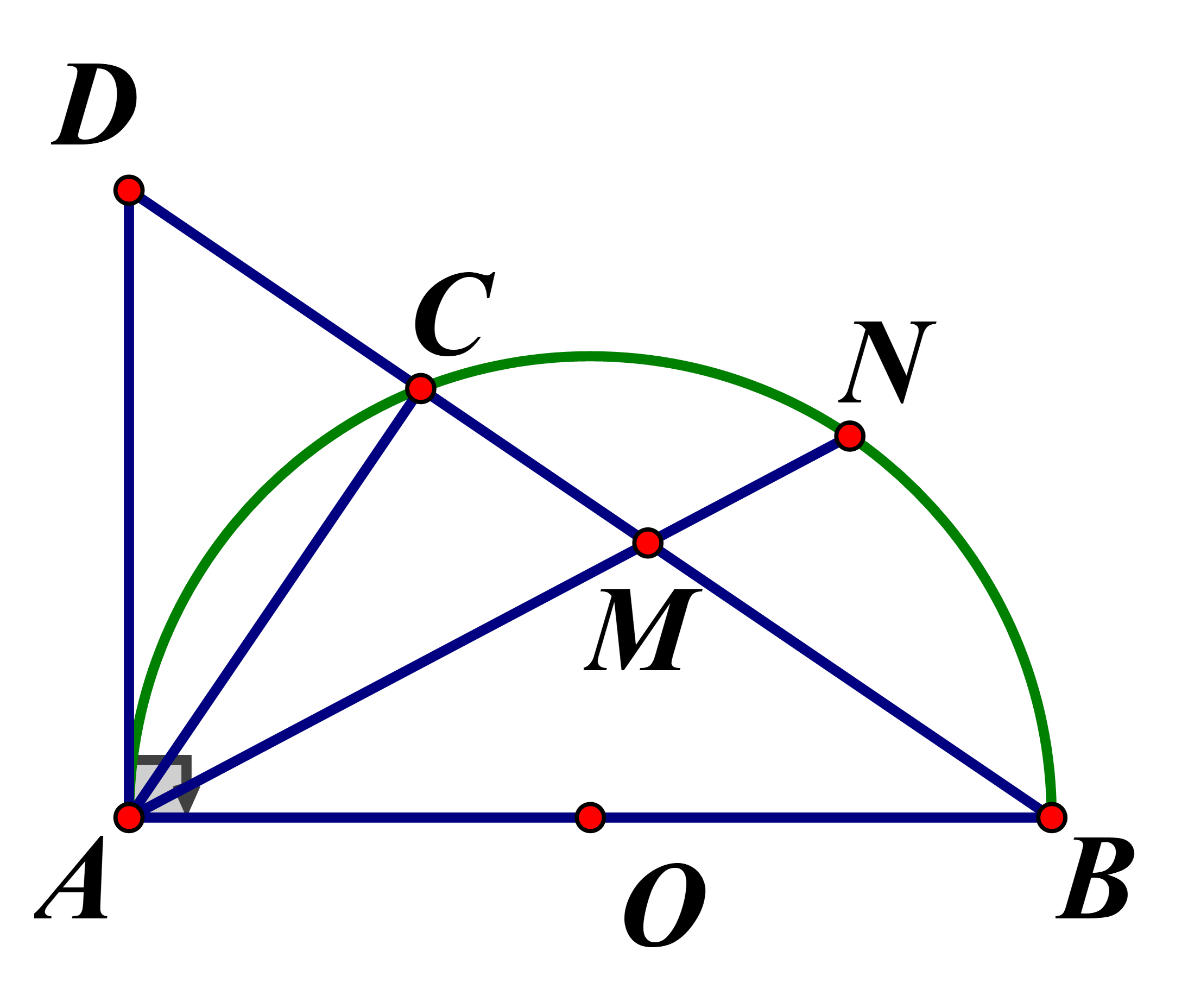
Ta có vlà tiếp tuyến nên
là góc có đỉnh trong đường tròn nên :
Mà là tia phân giác
Từ (1), (2), (3) cân nhưng không đều.
Chọn đáp án C
Câu 42:
Cho tam giác ABC có góc A bằng nội tiếp đường tròn kéo dài BA một đoạn Cho BC cố định, A di động trên cung chứa góc thuộc thì D di động trên đường nào ?
 Xem đáp án
Xem đáp án
Ta có : cân tại A
Mà BC cố định nên điểm D thuộc cung chứa góc dựng trên BC
Chọn đáp án B
Câu 43:
Cho tam giác nhọn ABC Đường tròn đường kính BC cắt AB và AC theo thứ tự tại D và E. Gọi H là giao điểm của BE và CD tia AH cắt BC tại F. Số tứ giác nội tiếp được đường tròn có trong hình vẽ là
 Xem đáp án
Xem đáp án
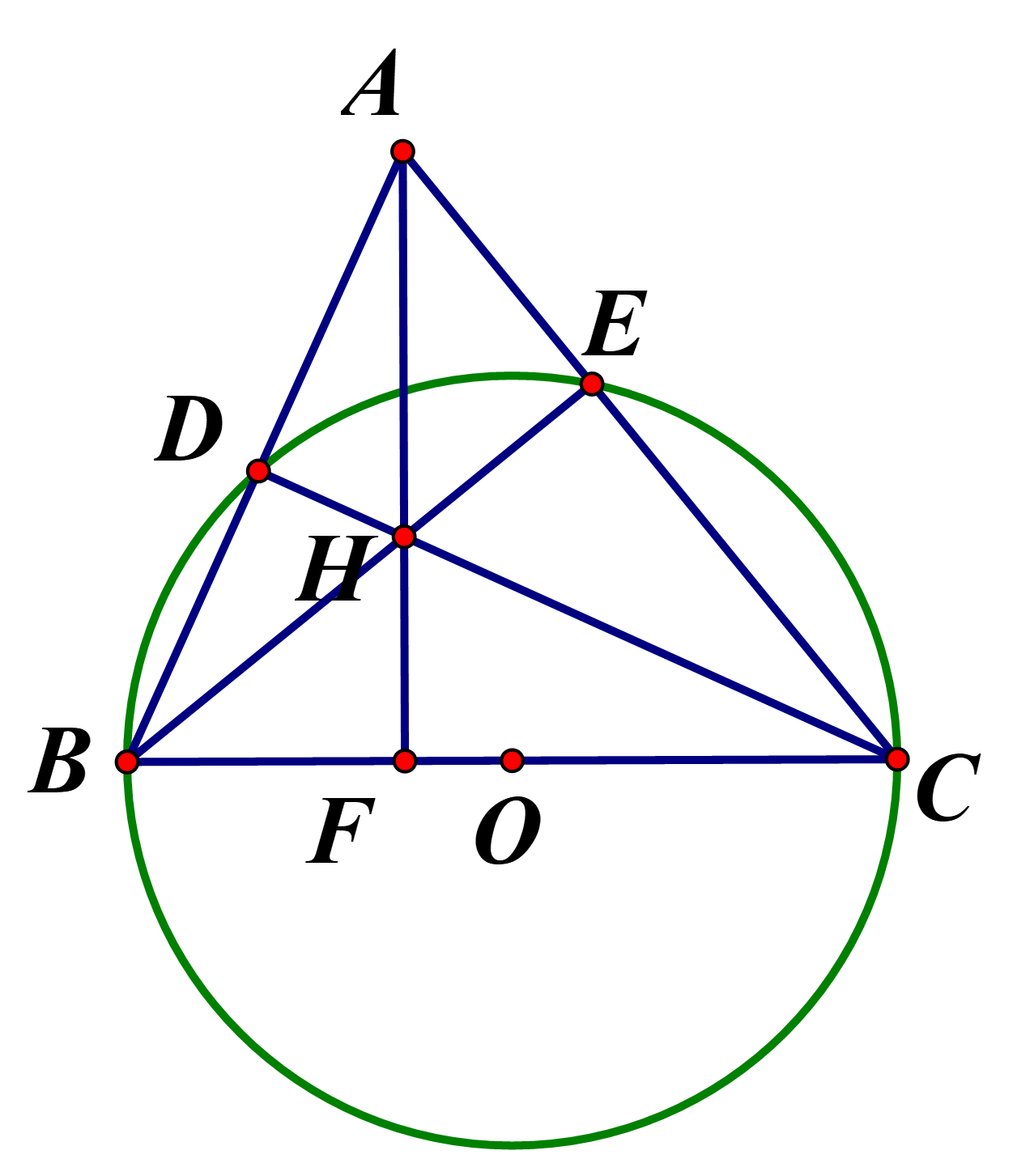
Các tứ giác nội tiếp :
Có 4 tứ giác nội tiếp Chọn đáp án A
Câu 44:
Cho tam giác ABC vuông tại A, đường cao AH nội tiếp đường tròn . Gọi I,K theo thứ tự là điểm đối xứng của H qua hai cạnh AB,AC Khẳng định nào sau đây đúng ?
 Xem đáp án
Xem đáp án
Cả 3 ý đều đúng. Chọn đáp án D
Câu 45:
Cho hai đường tròn và . Hai bán kính của đường tròn lớn cắt đường tròn nhỏ tại Cho biết góc Tính diện tích hình vành khăn nằm trong góc (hình giới hạn bởi hai đường tròn) (làm tròn kết quả đến chữ số thập phân thứ nhất)
 Xem đáp án
Xem đáp án
Diện tích hình vành khăn:
Chọn đáp án A
Câu 46:
Cho đường tròn (O;R) vẽ hai bán kính OA,OB vuông góc với nhau, tiếp tuyến của (O) tại A và B cắt nhau tại T Tính theo R diện tích hình giới hạn bởi hai tiếp tuyến TA,TB và cung nhỏ AB
 Xem đáp án
Xem đáp án
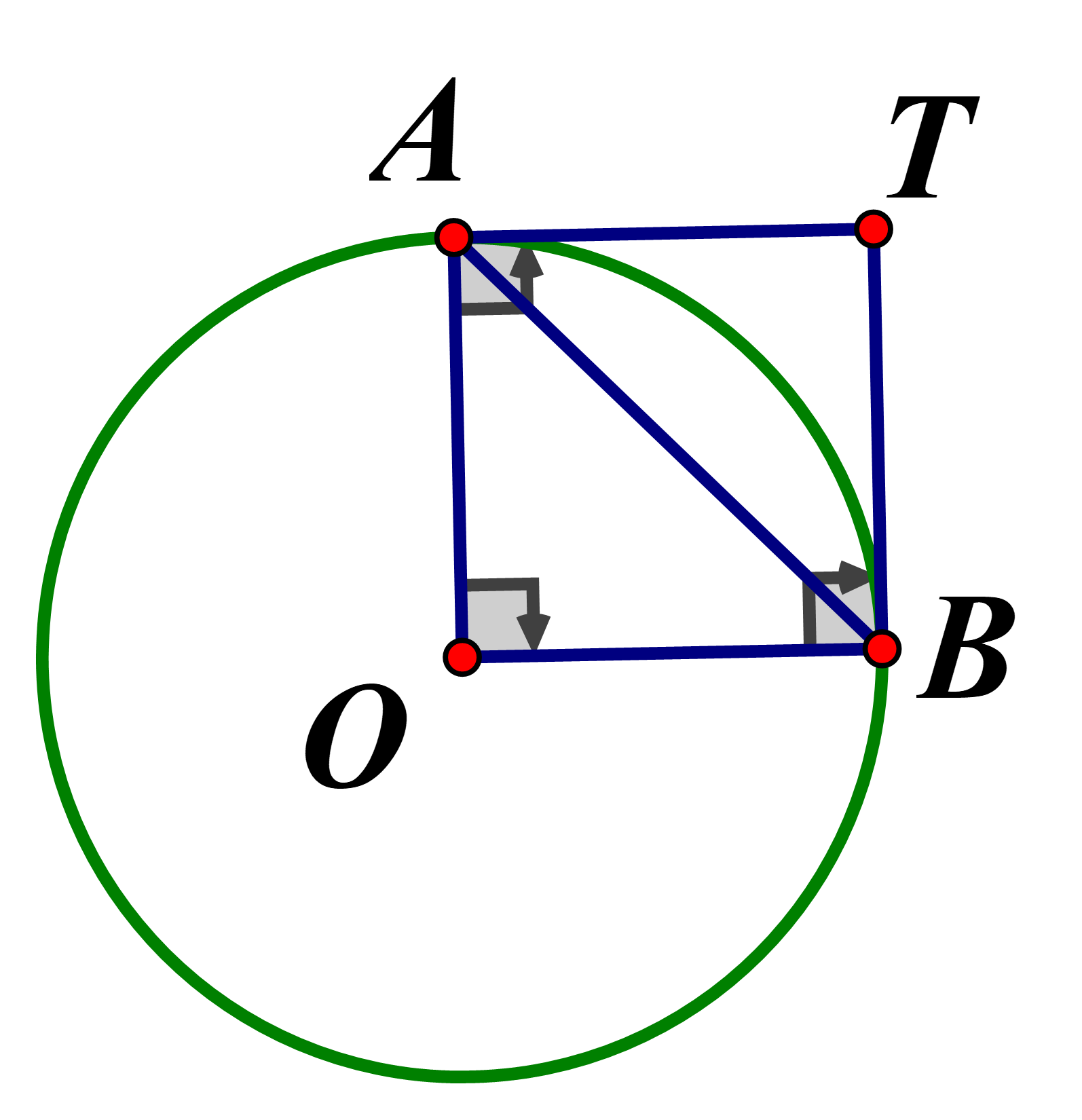
Ta có :
Từ (1) và (2) suy ra là hình vuông
Ta có:
Chọn đáp án A
Câu 47:
Cho hai đường tròn và tiếp xúc ngoài tại là tiếp tuyến chung ngoài, (B thuộc thuộc Tính số đo các góc
 Xem đáp án
Xem đáp án
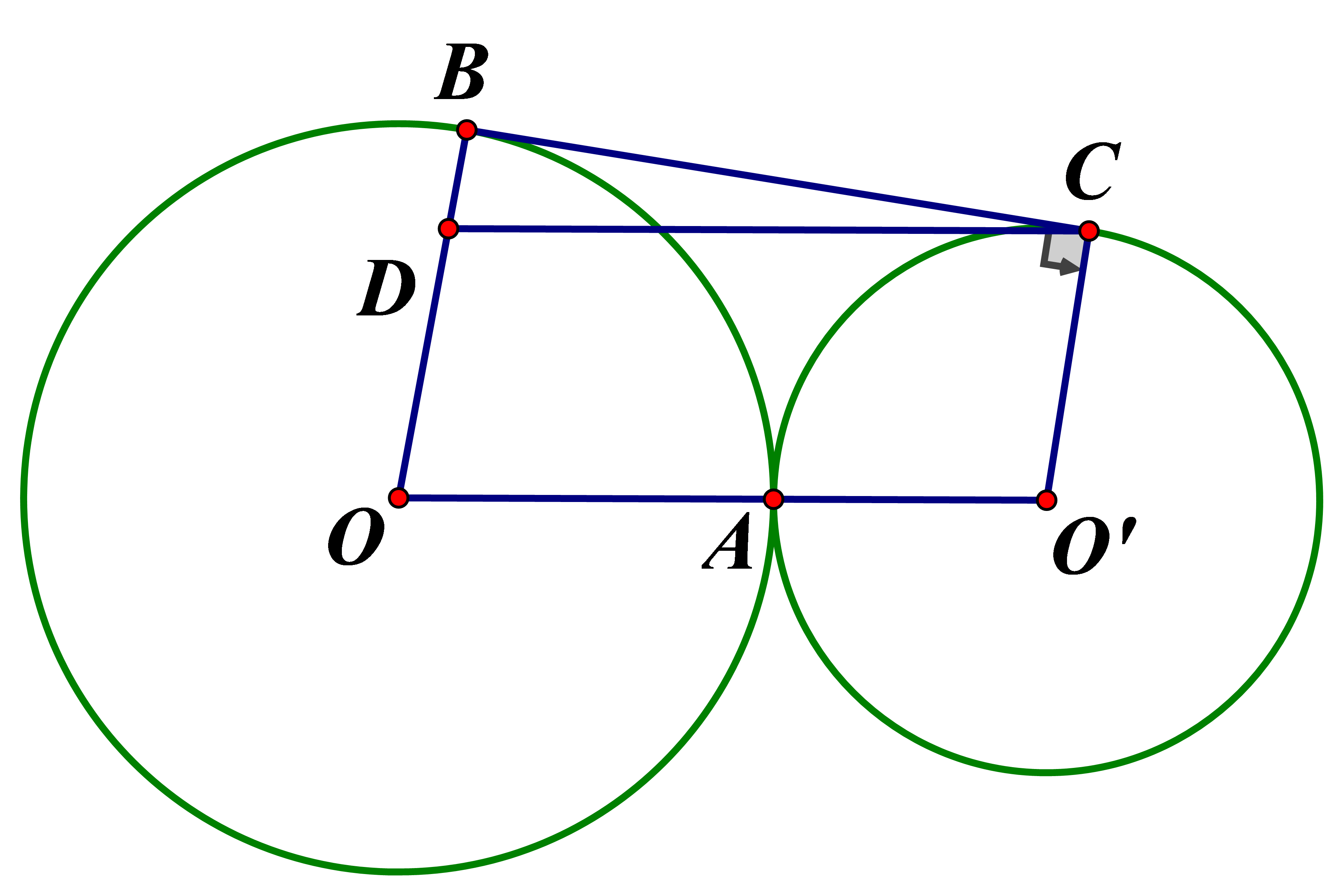
Ta có (tiếp tuyến vuông góc với bán kính đi qua tiếp điểm)
Vẽ
Tứ giác là hình bình hành
vuông tại B có nên bằng nửa tam giác đều cạnh CD
(hai góc đồng vị)
Ta có: (hai góc trong cùng phía)
Vậy Chọn đáp án C
Câu 48:
Từ 1 điểm M nằm ngoài đường tròn (O), vẽ hai cát tuyến MAB,MCD (A nằm giữa M và B, C nằm giữa M và D). Cho biết số đo cung nhỏ là và số đo cung nhỏ là Vậy số đo góc M là :
 Xem đáp án
Xem đáp án
Chọn đáp án D
Câu 49:
Một hình nón có diện tích xung quanh bằng và bán kính đáy Đường sinh của hình nón bằng:
 Xem đáp án
Xem đáp án
Ta có diện tích xung quanh của hình nón
Chọn đáp án A
Câu 50:
Cho hình vuông ABCD nội tiếp đường tròn (O;R) , cho hình vuông ABCD quay xung quanh đường trung trực của hai cạnh đối, thì phần thể tích của khối cầu nằm ngoài khối trụ là :
 Xem đáp án
Xem đáp án
Hình vuông ABCD nội tiếp (O;R) nên Khi quay mô hình ta được :
Hình cầu tâm O bán kính R và hình trụ có chiều cao bán kính đáy
Chọn dáp án B