Bộ 30 đề thi vào 10 môn Toán có lời giải chi tiết (Đề 15)
-
5639 lượt thi
-
50 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
Cho tam giác ABC vuông tại A đường cao AH .Hệ thức nào sau đây sai ?
 Xem đáp án
Xem đáp án
Áp dụng hệ thức lượng vào vuông tai A, đường cao AH
Hệ thức sai là Chọn đáp án A
Câu 2:
Cho vuông tại A đường cao AH .Có Độ dài cạnh AC bằng:
 Xem đáp án
Xem đáp án
Áp dụng hệ thức lượng ta có:
Chọn đáp án B
Câu 6:
Cho tam giác ABC vuông tại A, phân giác AD đường cao AH .Biết Độ dài BH là :
 Xem đáp án
Xem đáp án
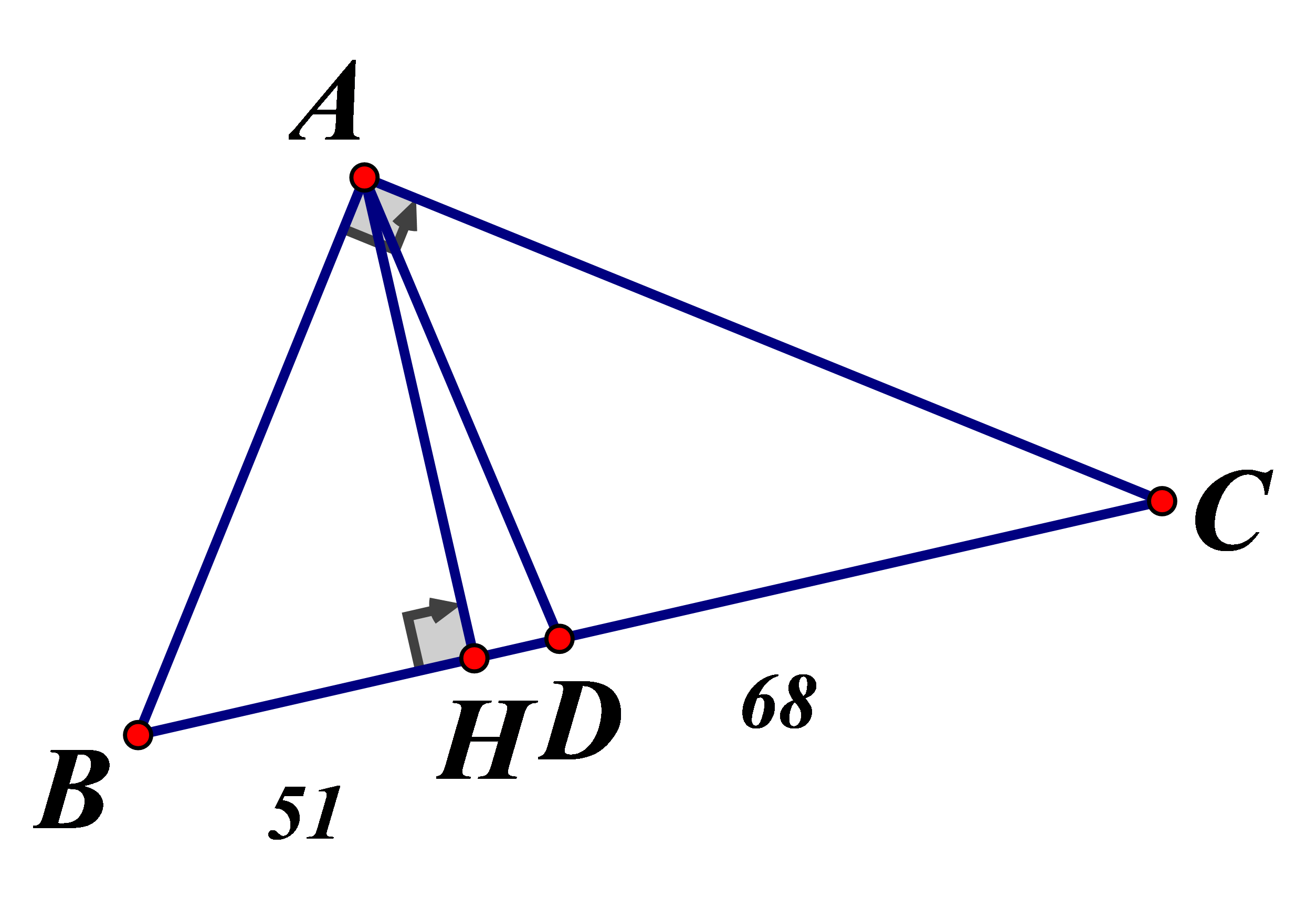
(tính chất đường phân giác)
. Áp dụng định lý Pytago:
(hệ thức lượng)
Hay
Chọn đáp án B
Câu 7:
Cho tam giác ABC đều có cạnh là 4cm .(O) là tâm đường tròn ngoại tiếp tam giác. Tính khoảng cách từ O đến BC
 Xem đáp án
Xem đáp án
Gọi H là trung điểm BC. Nên khoảng cách cần tìm là OH
Ta có :
Chọn đáp án A
Câu 8:
Cho đường tròn tâm O đường kính AB dây cung CD cắt AB tại M biết và Tính khoảng cách từ O đến CD
 Xem đáp án
Xem đáp án
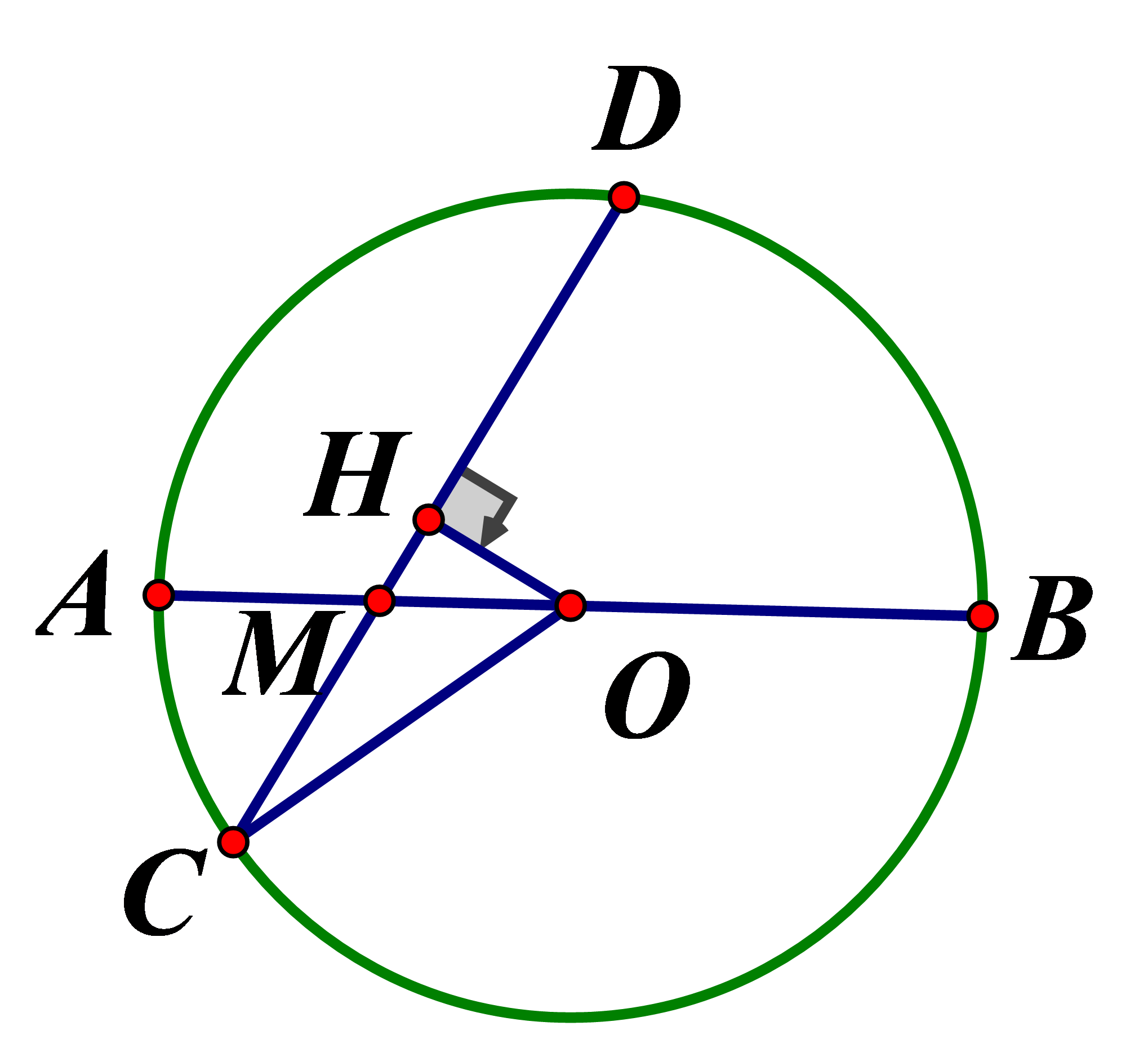
Kẻ
Do đó
có
Theo định lý Pytago ta có :
Chọn đáp án C
Câu 9:
Cho đường tròn (O) và hai điểm A,B nằm trên đường tròn. Biết góc Tính số đo cung nhỏ
 Xem đáp án
Xem đáp án
là góc ở tâm nên
Chọn đáp án B
Câu 10:
Cho hình vẽ. O là tâm đường tròn, biết Tính số đo
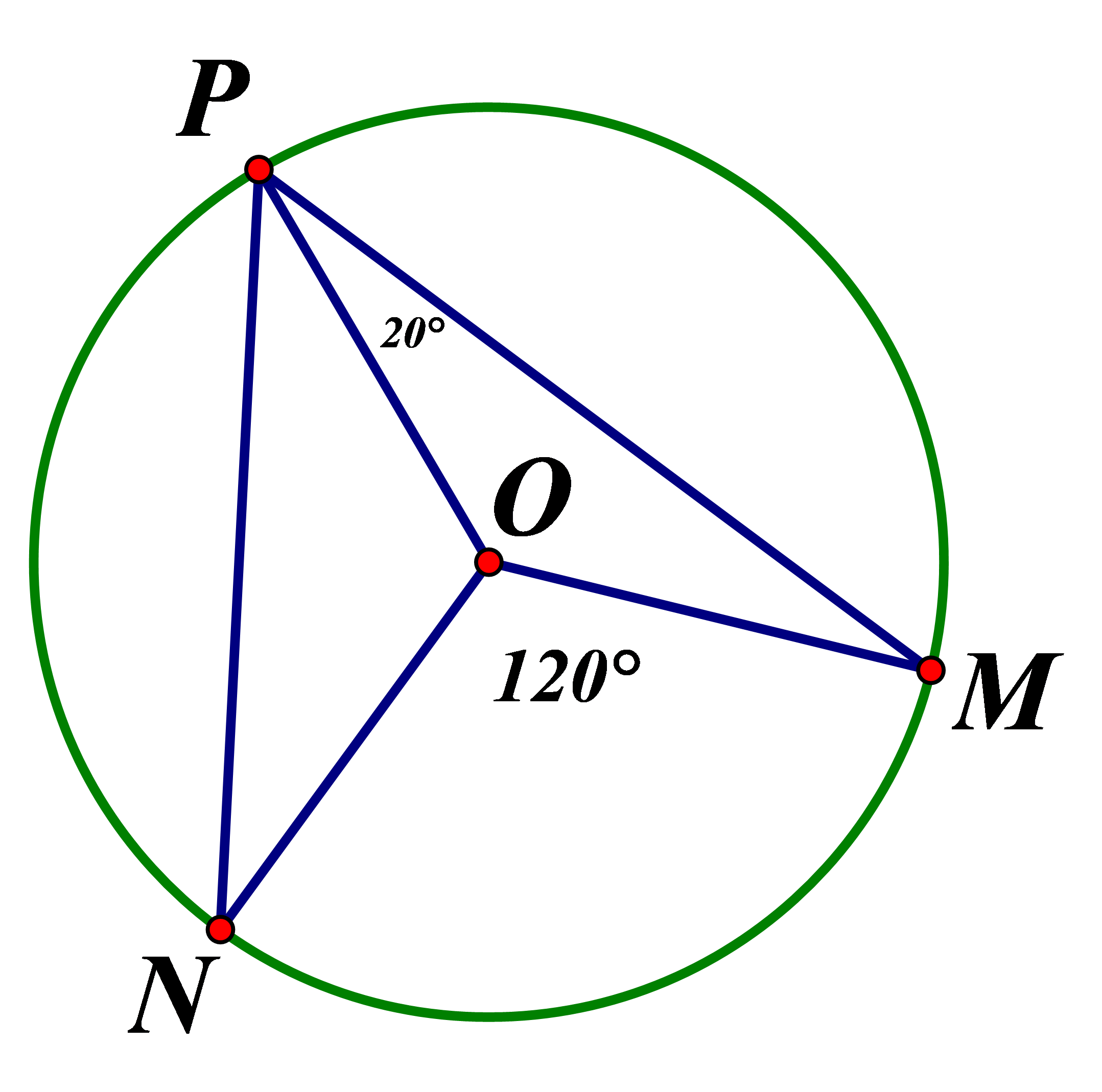
 Xem đáp án
Xem đáp án
là góc nội tiếp nên
Chọn đáp án A
Câu 11:
Cho hình vẽ. Biết (O) là tâm đường tròn, hai dây cắt nhau tại E, . Tính số đo

 Xem đáp án
Xem đáp án
là góc ở trong đường tròn nên
Chọn đáp án B
Câu 13:
 Xem đáp án
Xem đáp án
Thực hiện phép chia, ta có :
Thương là : dư là : Chọn đáp án B
Câu 15:
Hai phân thức nào sau đây không bằng nhau ?
 Xem đáp án
Xem đáp án
Ta thử lần lượt các phương án có:
Chọn đáp án A
Câu 18:
Từ phương trình , bằng cách sử dụng quy tắc chuyển vế để biến đổi ta có phương trình:
 Xem đáp án
Xem đáp án
Chọn đáp án A
Câu 24:
 Xem đáp án
Xem đáp án
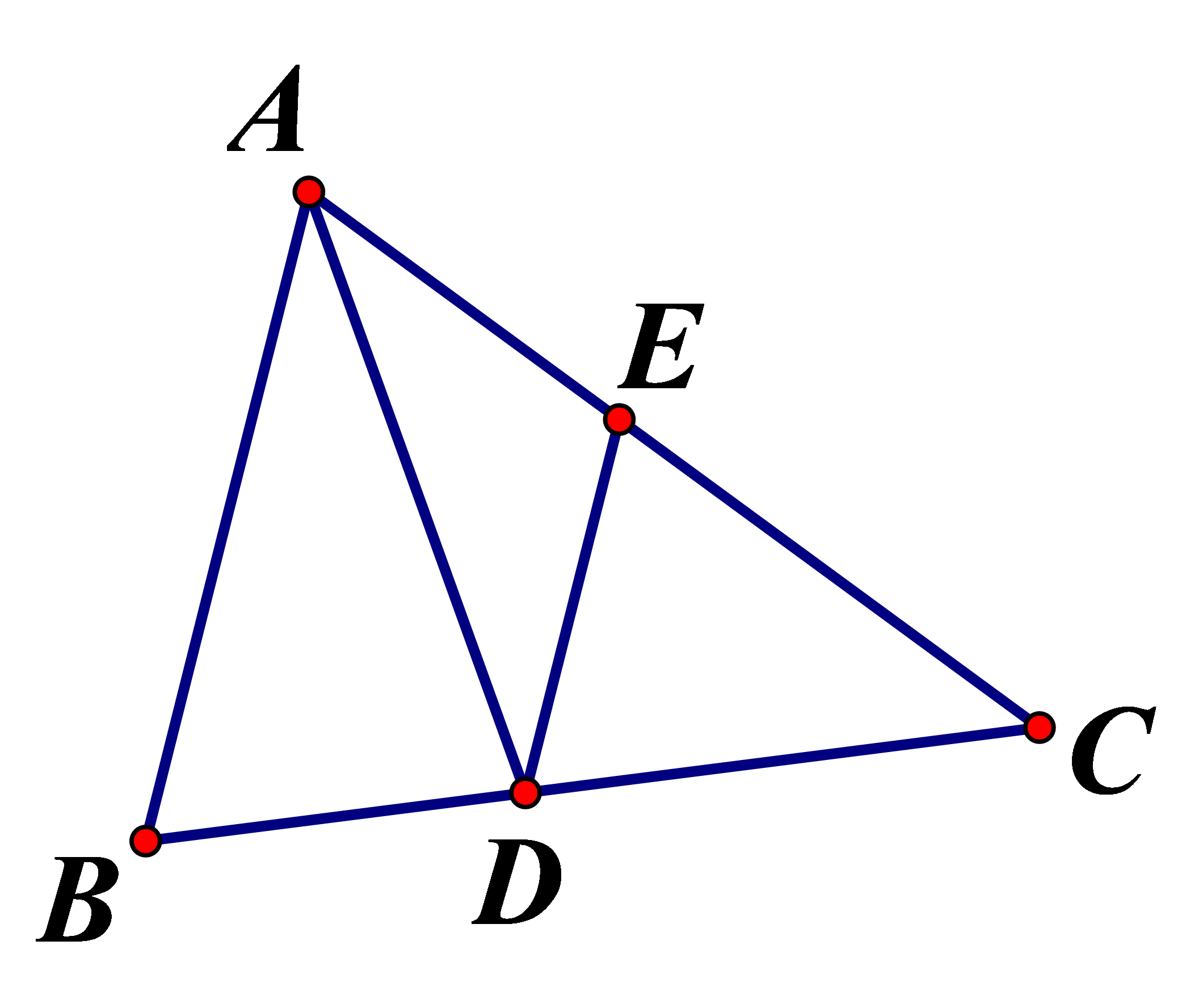
Vì AD là đường phân giác nên
Mà , theo hệ quả Ta let ta có:
Chọn đáp án A
Câu 26:
Cho hình vẽ sau. Biết . Tính diện tích tứ giác AEDF
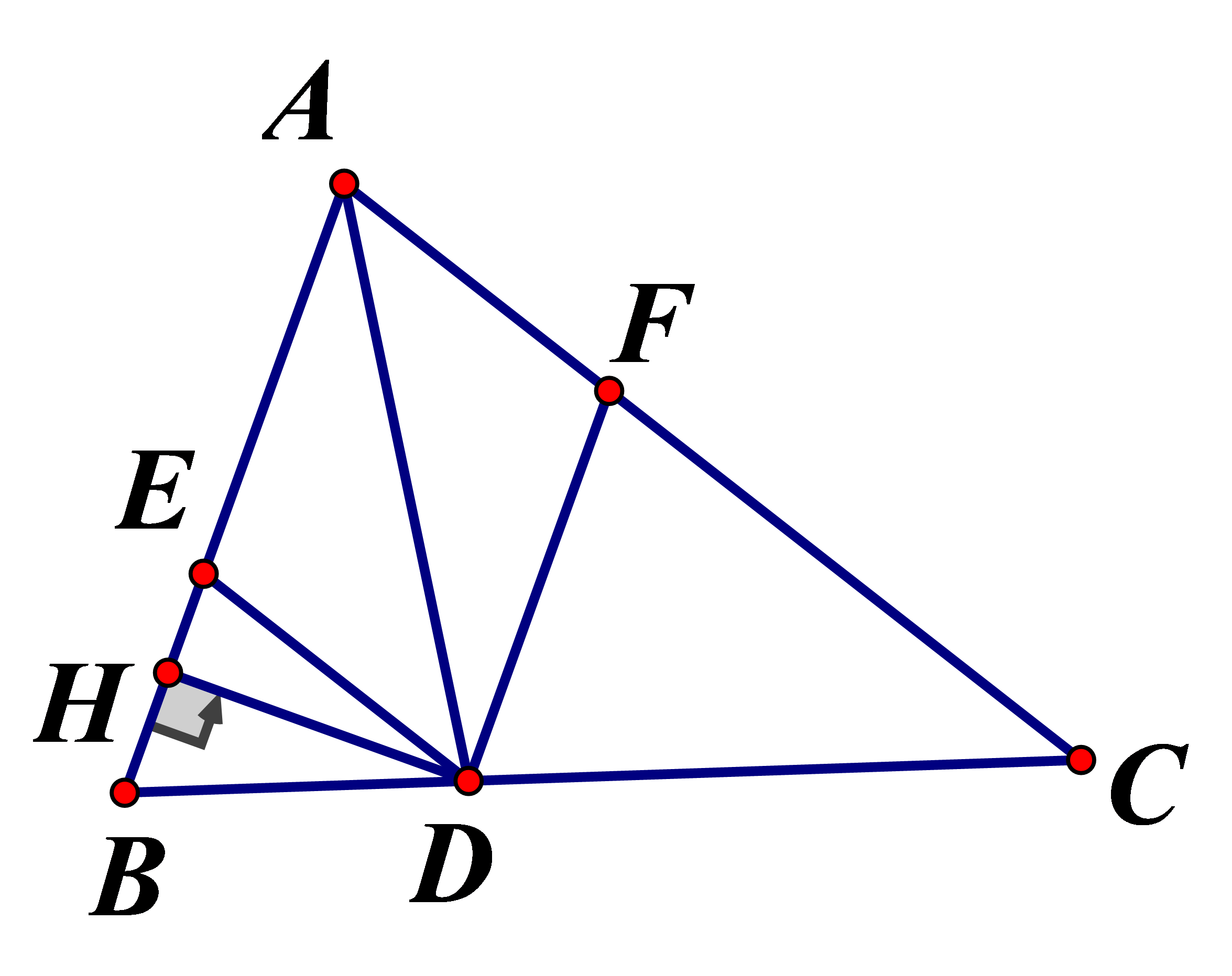
 Xem đáp án
Xem đáp án
Áp dụng hệ quả Ta let ta có:
Chọn đáp án A
Câu 27:
Cho AD là tia phân giác của thì :
 Xem đáp án
Xem đáp án
Áp dụng tính chất đường phân giác trong tam giác
Chọn đáp án B
Câu 31:
Cho có Đường phân giác trong cắt cạnh tại D. Biết Độ dài đoạn thẳng DC bằng:
 Xem đáp án
Xem đáp án
Vì AD là đường phân giác nên :
Chọn đáp án C
Câu 34:
Cho theo tỉ số đồng dạng Tỉ số chu vi của hai tam giác đó :
 Xem đáp án
Xem đáp án
Tỉ số chu vi bằng tỉ số đồng dạng . Chọn đáp án B
Câu 35:
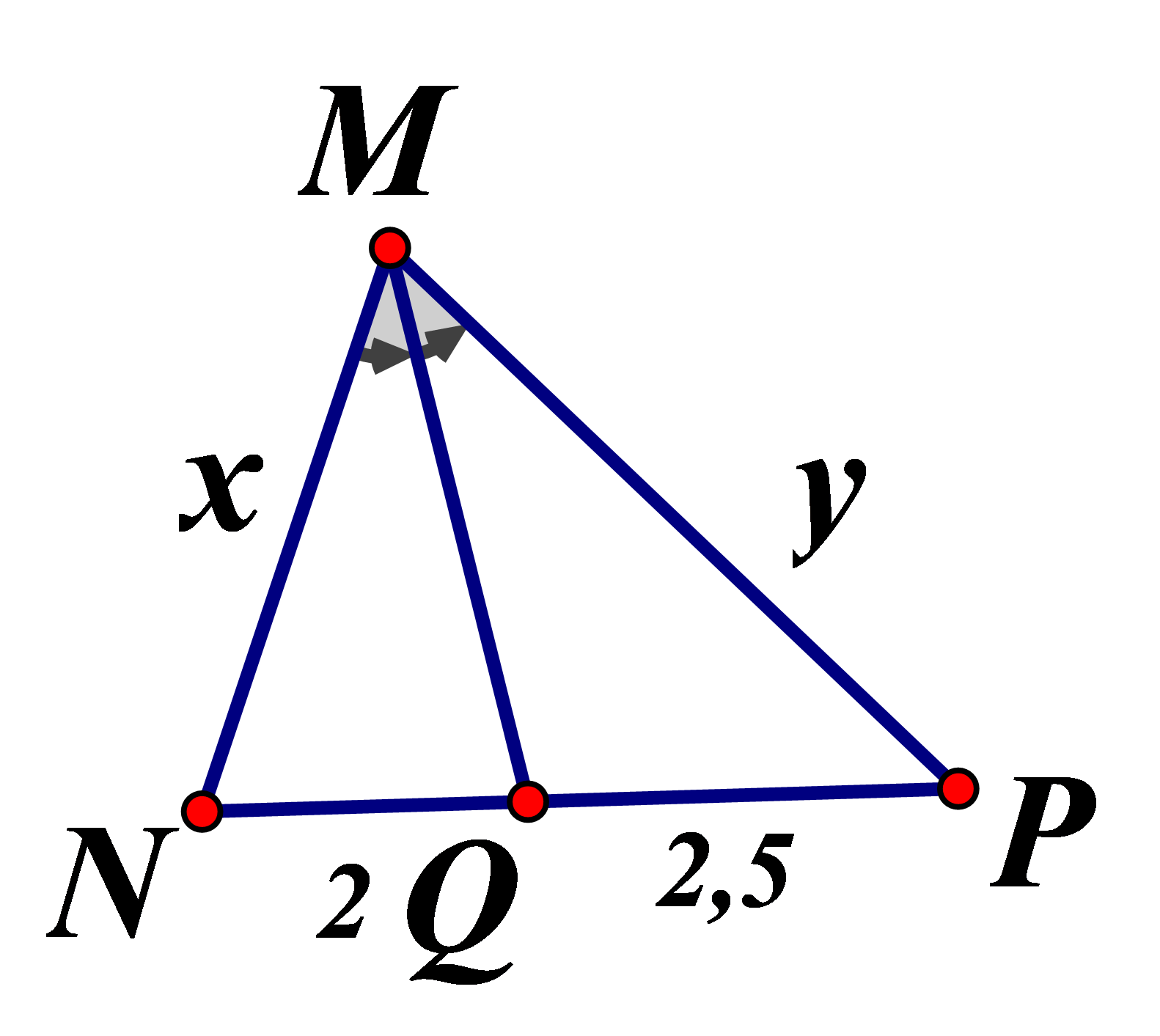
Trong hình biết MQ là tia phân giác của . Tỉ số là :
 Xem đáp án
Xem đáp án
Áp dụng tính chất đường phân giác trong tam giác
.Chọn đáp án D
Câu 37:
Trong hình vẽ cho biết Số đo của đoạn thẳng OM là :
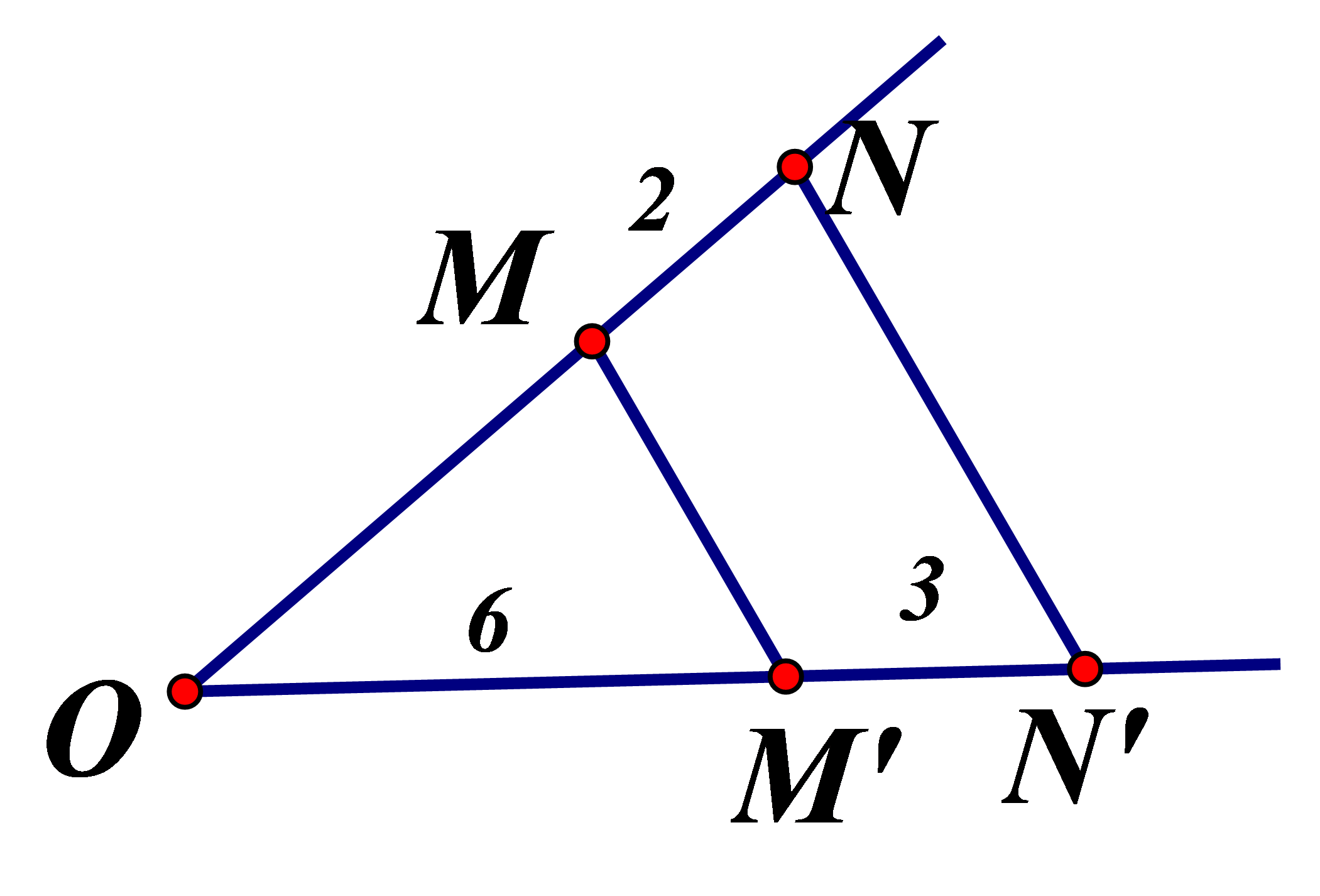
 Xem đáp án
Xem đáp án
Áp dụng định lý ta let khi ta có :
.Chọn đáp án D
Câu 38:
Cho hình vẽ bên. Hãy tính độ dài cạnh
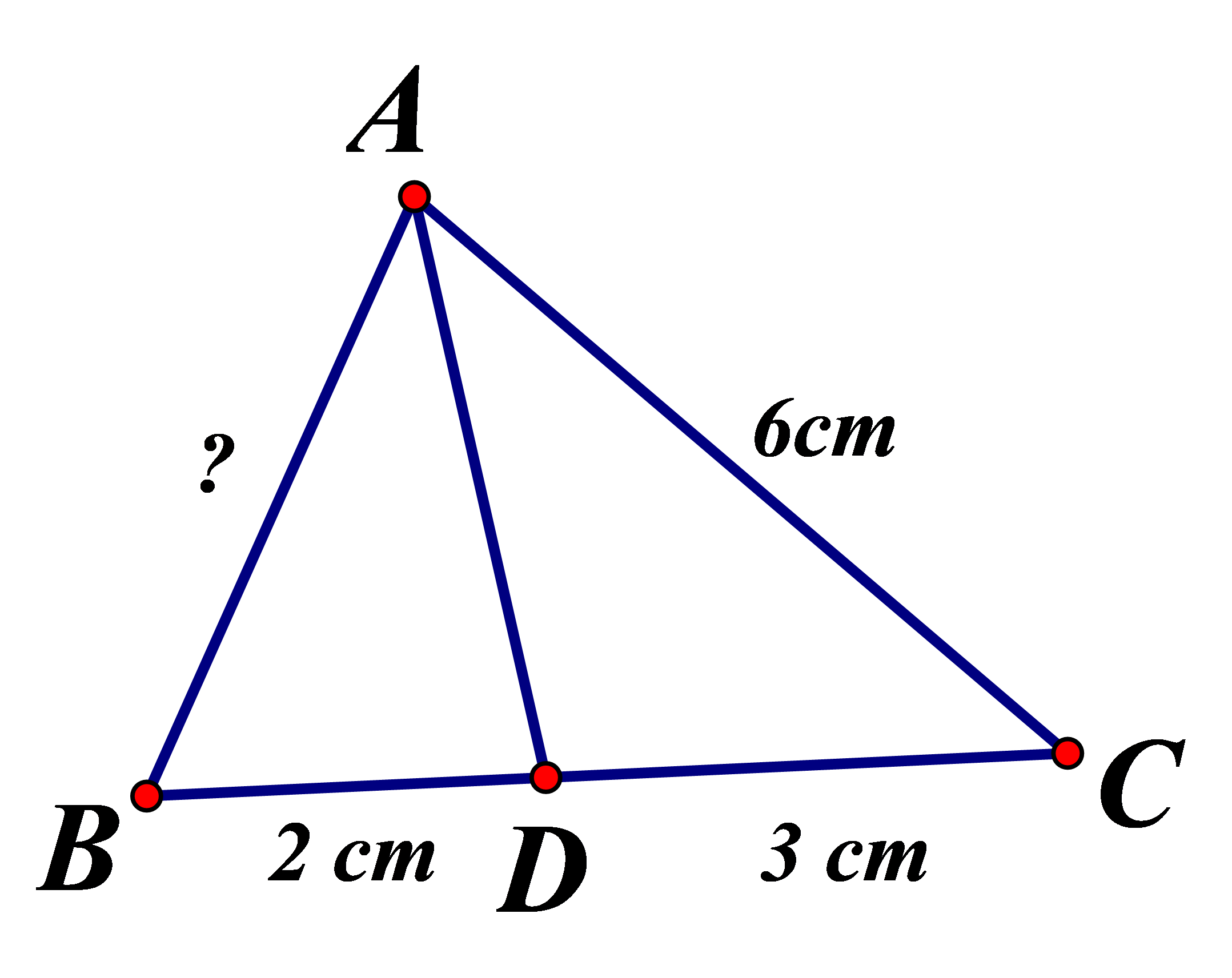
Chọn đáp án đúng trong các đáp án sau : Độ dài cạnh AB là :
 Xem đáp án
Xem đáp án
Vì AD là tia phân giác nên
Chọn đáp án A
Câu 39:
Cho tam giác ABC vuông tại A đường cao AH Hệ thức nào sau đây là đúng ?
 Xem đáp án
Xem đáp án
Áp dụng hệ thức lượng vào tam giác ABC vuông tại A đường cao AH nên .Chọn đáp án B
Câu 40:
Cho tam giác ABC vuông tại A đường cao AH .Hệ thức nào sau đây là đúng ?
 Xem đáp án
Xem đáp án
Áp dụng hệ thức lượng vào tam giác ABC vuông tại A đường cao AH nên Chọn đáp án C
Câu 44:
Cho tam giác ABC vuông tại A, đường cao AH .Biết Độ dài đường cao AH bằng:
 Xem đáp án
Xem đáp án
Áp dụng hệ thức lượng vào vuông tại A, đường cao AH ta có:
Chọn đáp án B
Câu 45:
Cho tam giác ABC vuông tại A, ta có ta có bằng
 Xem đáp án
Xem đáp án
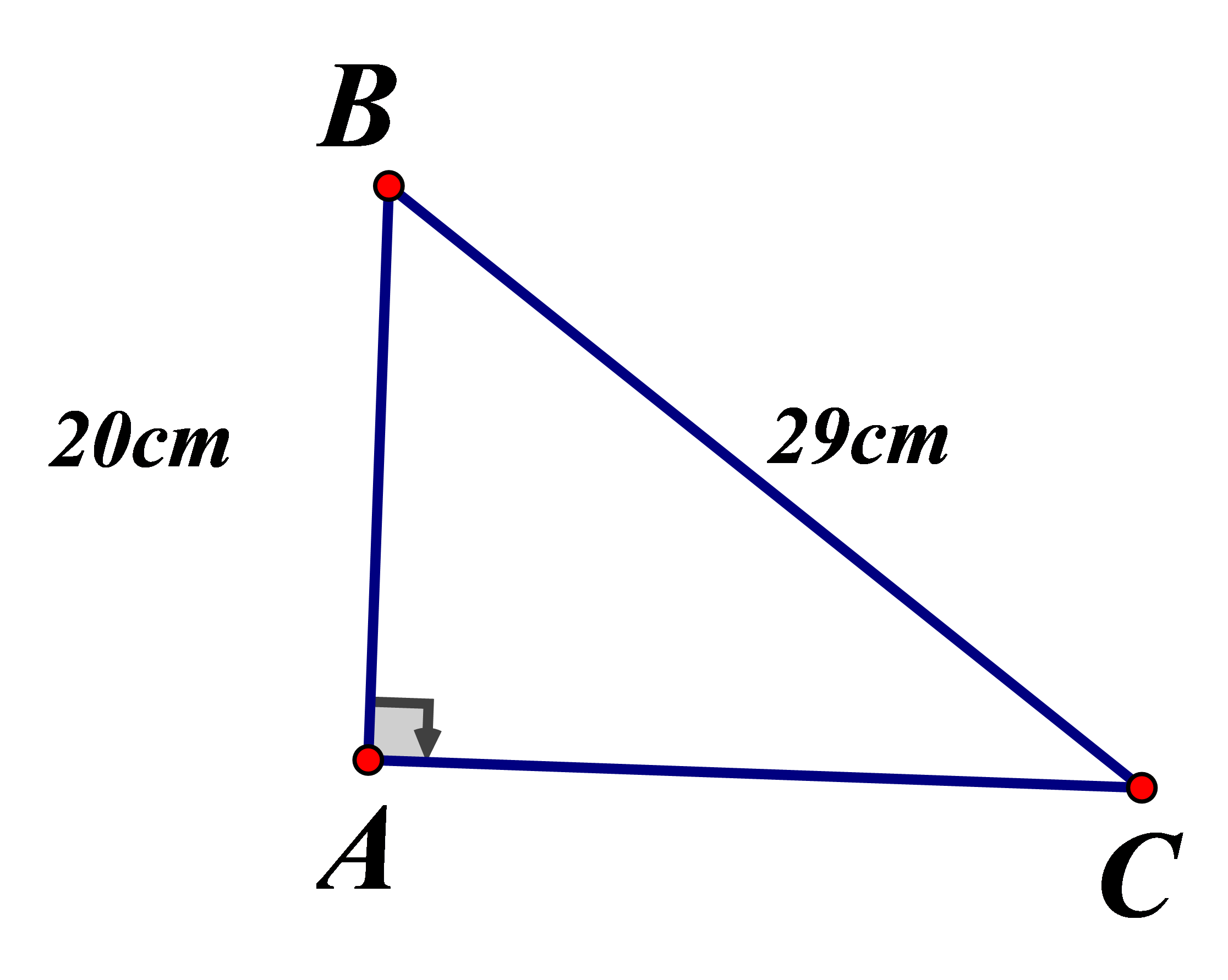
Áp dụng định lý Pytago:
.Chọn đáp án C
Câu 46:
Hàm số nào sau đây không phải là hàm số bậc nhất ?
 Xem đáp án
Xem đáp án
Hàm số bậc nhất có dạng nên chọn đáp án A
Chọn đáp án A
Câu 48:
Với giá tri nào của a,b thì đường thẳng đi qua điểm và song song với đường thẳng
 Xem đáp án
Xem đáp án
đường thẳng song song với đường thẳng
Nên
Chọn đáp án A
Câu 49:
 Xem đáp án
Xem đáp án
Để đường thẳng và trùng nhau thì
Chọn đáp án A
Câu 50:
Với giá trị nào của a thì đường thẳng vuông góc với đường thẳng
 Xem đáp án
Xem đáp án
đường thẳng vuông góc với đường thẳng
Khi Chọn đáp án A