49 câu hỏi trắc nghiệm thuộc Bộ 30 đề thi vào 10 môn Toán có lời giải chi tiết (Đề 5)

Câu 1:

Cho biểu thức $P = \sqrt{(6 \sqrt{\frac{4}{25}} - \sqrt{\frac{9}{25}}) .15} .$ Mệnh đề nào sau đây đúng ?

$A . G i á t r ị c ủ a P b i ể u t h ứ c l à s ố n g u y ê n$

$B . G i á t r ị c ủ a b i ể u t h ứ c P l à s ố h ữ u t ỉ$

$C . G i á t r ị c ủ a b i ể u t h ứ c P l à s ố v ô t ỉ$

$D . G i á t r ị c ủ a b i ể u t h ứ c P l à s ố n g u y ê n d ư ơ n g$

$\begin{array}{l} P = \sqrt{(6 \sqrt{\frac{4}{25}} - \sqrt{\frac{9}{25}}) .15} = \sqrt{(6. \frac{2}{5} - \frac{3}{5}) .15} = \sqrt{(\frac{12}{5} - \frac{3}{5}) .15} \\ = \sqrt{\frac{9}{5} .15} = \sqrt{27} = 3 \sqrt{3} \end{array}$

Nên P là số vô tỉ. Chọn đáp án C

Câu 2:

Cho $M = \frac{m - \sqrt{m} - 2}{m - 1} .$ Với $m = 0,$ so sánh M với $a = \sqrt{2 + \sqrt{2 + \sqrt{2 + \sqrt{2}}}}$

$A . M > a$

$B . M < a$

$C . M \leq a$

$D . M \geq a$

Xem đáp án

Thay $m = 0$ vào M ta được:

$\begin{array}{l} M = \frac{0 - \sqrt{0} - 2}{0 - 1} = 2 = \sqrt{4} = \sqrt{2 + 2} = \sqrt{2 + \sqrt{4}} \\ = \sqrt{2 + \sqrt{2 + 2}} = \sqrt{2 + \sqrt{2 + \sqrt{4}}} = \sqrt{2 + \sqrt{2 + \sqrt{2 + 2}}} \\ = \sqrt{2 + \sqrt{2 + \sqrt{2 + \sqrt{4}}}} > \sqrt{2 + \sqrt{2 + \sqrt{2 + \sqrt{2}}}} \Rightarrow M > a \end{array}$

Chọn đáp án A

Câu 3:

Cho $A = \frac{1}{\sqrt{1} + \sqrt{2}} + \frac{1}{\sqrt{2} + \sqrt{3}} + \frac{1}{\sqrt{3} + \sqrt{4}}$ . Tìm nghiệm của phương trình $A x^{2} + 3 A x - 4 = 0$

$A . [\begin{array}{l} x = - 4 \\ x = 1 \end{array}$

$B . [\begin{array}{l} x = 4 \\ x = - 1 \end{array}$

$C . [\begin{array}{l} x = \sqrt{2} + 1 \\ x = \sqrt{2} - 1 \end{array}$

$D . [\begin{array}{l} x = 2 \sqrt{3} \\ x = 1 \end{array}$

Xem đáp án

$A = \frac{1}{\sqrt{1} + \sqrt{2}} + \frac{1}{\sqrt{2} + \sqrt{3}} + \frac{1}{\sqrt{3} + \sqrt{4}} = 1$

Nghiệm của phương trình $A x^{2} + 3 A x - 4 = 0 \Leftrightarrow x^{2} + 3 x - 4 = 0 \Leftrightarrow [\begin{array}{l} x = 1 \\ x = - 4 \end{array}$

Chọn đáp án A

Câu 4:

Cho $B = \frac{1}{\sqrt{1} + \sqrt{2}} + \frac{1}{\sqrt{2} + \sqrt{3}} + ..... + \frac{1}{\sqrt{98} + \sqrt{99}} + \frac{1}{\sqrt{99} + \sqrt{100}} .$ Số nghiệm của phương trình $x^{3} + 3 B x^{2} + 27 B x + 9 B^{2} = 0$ là :

$A .0$

$B .1$

$C .2$

$D .3$

Xem đáp án

$B = \frac{1}{\sqrt{1} + \sqrt{2}} + \frac{1}{\sqrt{2} + \sqrt{3}} + ...... + \frac{1}{\sqrt{99} + \sqrt{100}}$

Xét $\frac{1}{\sqrt{k} + \sqrt{k + 1}} = \frac{\sqrt{k + 1} - \sqrt{k}}{k + 1 - k} = \sqrt{k + 1} - \sqrt{k}$

$\Rightarrow B = \sqrt{2} - \sqrt{1} + \sqrt{3} - \sqrt{2} + ..... + \sqrt{100} - \sqrt{99} = \sqrt{100} - \sqrt{1} = 9$ nên phương trình trở thành :

$x^{3} + 27 x^{2} + 243 x + 729 = 0 \Leftrightarrow {(x + 9)}^{3} = 0 \Leftrightarrow x = - 9$ , nên phương trình có 1 nghiệm. Chọn câu B

Câu 5:

Rút gọn $N = (\frac{\sqrt{x}}{x - 4} + \frac{1}{\sqrt{x} - 2}) . \frac{\sqrt{x} - 2}{2},$ ta được kết quả $N = \frac{\sqrt{x} + 1}{\sqrt{x} + 2}$ . Tìm tất cả các giá trị của x để $N = \frac{3}{4} :$

$A . x = 4$

$B . x = 1$

$C . x = 9$

$D . K h ô n g t ồ n t ạ i x$

Xem đáp án

$\frac{\sqrt{x} + 1}{\sqrt{x} + 2} = \frac{3}{4} (\begin{array}{l} x > 0 \\ x \neq 4 \end{array}) \Leftrightarrow 4 \sqrt{x} + 4 = 3 \sqrt{x} + 6 \Leftrightarrow \sqrt{x} = 2 \Rightarrow x = 4 (k t m)$

Chọn đáp án D

Câu 6:

Hàm số $y = x + |x|$ được viết lại :

$A . y = \{\begin{cases} x k h i x \leq 0 \\ 2 x k h i x > 0 \end{cases}$

$B . y = \{\begin{cases} 0 k h i x \leq 0 \\ 2 x k h i x > 0 \end{cases}$

$C . y = \{\begin{cases} 2 x k h i x \leq 0 \\ 0 k h i x > 0 \end{cases}$

$D . y = \{\begin{cases} - 2 x k h i x \leq 0 \\ 0 k h i x > - 2 \end{cases}$

Xem đáp án

$y = x + |x| = [\begin{array}{l} y = x - x (x < 0) \\ y = x + x (x > 0) \end{array} \Leftrightarrow [\begin{array}{l} y = 0 \\ y = 2 x \end{array}$

Chọn đáp án B

Câu 7:

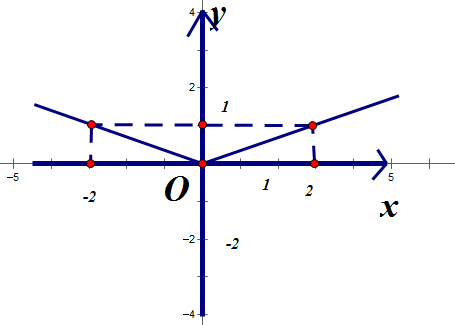
Đồ thị hinh trên biểu diễn hàm số nào sau đây :

$A . y = 2 x - 2$

$B . y = x - 2$

$C . y = - 2 x - 2$

$D . y = - x - 2$

Xem đáp án

Đồ thị hàm số $y = a x + b$ đi qua $(1; 0); (0; - 2)$ nên $\{\begin{cases} a + b = 0 \\ b = - 2 \end{cases} \Leftrightarrow \{\begin{cases} a = 2 \\ b = - 2 \end{cases} \Rightarrow y = 2 x - 2$ . Chọn đáp án A

Câu 8:

Đồ thị trong hình vẽ biểu diễn hàm số nào sau đây ?

Media VietJack

$A . y = |x|$

$B . y = |2 x|$

$C . y = |\frac{1}{2} x|$

$D . y = |3 - x|$

Xem đáp án

$y = 1 \Leftrightarrow x = |2| \Rightarrow y = \frac{1}{2} |x|$

Chọn đáp án C

Câu 9:

Phương trình đường thẳng đi qua hai điểm $A (3; 1)$ và $B (- 2; 6)$ là :

$A . y = - x + 4$

$B . y = - x + 6$

$C . y = 2 x + 2$

$D . y = x - 4$

Xem đáp án

Đồ thị $y = a x + b$ đi qua hai điểm $A (3; 1)$ và $B (- 2; 6)$

$\Rightarrow \{\begin{cases} 3 a + b = 1 \\ - 2 a + b = 6 \end{cases} \Leftrightarrow \{\begin{cases} a = - 1 \\ b = 4 \end{cases}$ $\Rightarrow y = - x + 4$ . Chọn đáp án A

Câu 10:

Trong mặt phẳng $O x y$ cho đường thẳng $(d)$ có phương trình $y = k x + k^{2} - 3.$ Tìm k để đường thẳng d đi qua gốc tọa độ O

$A . k = \sqrt{3}$

$B . k = \sqrt{2}$

$C . k = - \sqrt{2}$

$D . [\begin{array}{l} k = \sqrt{3} \\ k = - \sqrt{3} \end{array}$

Xem đáp án

Để đường thẳng d đi qua gốc tọa độ $\Leftrightarrow k^{2} - 3 = 0 \Leftrightarrow k = \pm \sqrt{3}$

Chọn đáp án D

Câu 11:

Phương trình đường thẳng đi qua giao điểm của $y = 2 x + 1$ và $y = 3 x - 4$ và song song với đường thẳng $y = \sqrt{2} x + 15$ là :

$A . y = \sqrt{2} x + 11 - 5 \sqrt{2}$

$B . y = x + 5 \sqrt{2}$

$C . y = \sqrt{6} x - 5 \sqrt{2}$

$D . y = 4 x + \sqrt{2}$

Xem đáp án

Ta có : $\{\begin{cases} y = 2 x + 1 \\ y = 3 x - 4 \end{cases} \Leftrightarrow \{\begin{cases} x = 5 \\ y = 11 \end{cases} \Rightarrow A (5; 11)$

Đường thẳng $d / / d' : y = x \sqrt{2} + 15 \Rightarrow d : y = x \sqrt{2} + m (m \neq 15)$

Mà $d$ qua $A (5; 11) \Rightarrow 5 \sqrt{2} + m = 11 \Rightarrow d : y = x \sqrt{2} + 11 - 5 \sqrt{2}$

Chọn đáp án A

Câu 12:

Tìm tất cả các giá trị của tham số m để đường thẳng $d : y = (3 m + 2) x - 7 m - 1$ vuông góc với đường thẳng $Δ : y = 2 x - 1$

$A . m = 0$

$B . m = - \frac{5}{6}$

$C . m < \frac{5}{6}$

$D . m > - \frac{1}{2}$

Xem đáp án

Để đường thẳng $d : y = (3 m + 2) x - 7 m - 1$ vuông góc với đường thẳng $Δ : y = 2 x - 1$ thì $(3 m + 2) .2 = - 1 \Leftrightarrow m = - \frac{5}{6}$ .Chọn đáp án B

Câu 13:

Biết rằng đồ thị hàm số $y = a x + b$ đi qua điểm $A (- 3; 1)$ và có hệ số góc là -2 Tính tích $P = a b$

$A . P = - 10$

$B . P = 10$

$C . P = - 7$

$D . P = - 5$

Xem đáp án

Hệ số góc bằng $- 2 \Rightarrow a = - 2$

Đồ thị đi qua điểm $A (- 3; 1) \Rightarrow - 3 a + b = 1 \Leftrightarrow - 3. (- 2) + b = 1 \Leftrightarrow b = - 5$

Vậy $P = (- 2) . (- 5) = 10.$ Chọn đáp án B

Câu 14:

Tìm giá trị thực của m để hai đường thẳng $d : y = m x - 3$ và $Δ : y + x = m$ cắt nhau tại một điểm nằm trên trục tung

$A . m = - 3$

$B . m = 3$

$C . m = \pm 3$

$D . m = 0$

Xem đáp án

Gọi $A (0; a)$ là giao điểm hai đường thẳng nằm trên trục tung

$\Rightarrow \{\begin{cases} A \in d \\ A \in Δ \end{cases} \Leftrightarrow \{\begin{cases} a = 0. m - 3 \\ a + 0 = m \end{cases} \Leftrightarrow \{\begin{cases} a = - 3 \\ m = - 3 \end{cases}$ Chọn đáp án A

Câu 15:

Tìm tất cả các giá trị thực của m để hai đường thẳng $d : y = m x - 3$ và $Δ : y + x = m$ cắt nhau tại một điểm nằm trên trục hoành

$A . m = \sqrt{3}$

$B . m = \pm \sqrt{3}$

$C . m = - \sqrt{3}$

$D . m = 3$

Xem đáp án

Gọi $B (b; 0)$ là giao điểm hai đường thẳng nằm trên trục hoành

$\Rightarrow \{\begin{cases} B \in d \\ B \in Δ \end{cases} \Rightarrow \{\begin{cases} 0 = m . b - 3 \\ 0 + b = m \end{cases} \Leftrightarrow \{\begin{cases} b^{2} = 3 \\ b = m \end{cases} \Leftrightarrow [\begin{array}{l} b = m = \sqrt{3} \\ b = m = - \sqrt{3} \end{array}$

Chọn đáp án B

Câu 16:

Tìm phương trình đường thẳng $d : y = a x + b .$ Biết đường thẳng d đi qua điểm $I (1; 2)$ và tạo với hai tia $O x, O y$ một tam giác có diện tích bằng 4

$A . y = - 2 x - 4$

$B . y = - 2 x + 4$

$C . y = 2 x - 4$

$D . y = 2 x + 4$

Xem đáp án

Đường thẳng $d : y = a x + b$ đi qua điểm $I (1; 2)$ nên $2 = a + b (1)$

Ta có: $d \cap O x = A (- \frac{b}{a}; 0); d \cap O y = B (O; b)$

Suy ra $O A = |- \frac{b}{a}| = - \frac{b}{a}$ và $O B = |b| = b$ (Do $A, B$ thuộc hai tia $O x, O y)$

$Δ O A B$ vuông tại O. Do đó, ta có: $S_{A B C} = \frac{1}{2} . O A . O B = 4$ nên ta có:

$\frac{1}{2} (- \frac{b}{a}) . b = 4 \Leftrightarrow b^{2} = - 8 a (2)$

Từ (1) suy ra $b = 2 - a .$ Thay vào ta được :

${(2 - a)}^{2} = - 8 a \Leftrightarrow a^{2} - 4 a + 4 = - 8 a \Leftrightarrow a^{2} + 4 a + 4 = 0 \Leftrightarrow a = - 2$

Với $a = - 2 \Rightarrow b = 4.$ Vậy đường thẳng cần tìm là : $y = - 2 x + 4.$

Chọn đáp án B

Câu 17:

Hệ phương trình nào sau đây vô nghiệm

$A . \{\begin{cases} x - 2 y = 5 \\ - \frac{1}{2} x + y = 3 \end{cases}$

$B . \{\begin{cases} x - 2 y = 5 \\ \frac{1}{2} x + y = 3 \end{cases}$

$C . \{\begin{cases} x - 2 y = 5 \\ - \frac{1}{2} x + y = - \frac{5}{2} \end{cases}$

$D . \{\begin{cases} x - 2 y = 5 \\ - \frac{1}{2} x - y = 3 \end{cases}$

Xem đáp án

Hệ phương trình $\frac{a}{a'} = \frac{b}{b'} \neq \frac{c}{c'}$ vô nghiệm khi .Chọn đáp án A

Câu 18:

Cho các đường thẳng $d_{1} : y = 2 x + 1, d_{2} : y = x + 2, y = (m^{2} + 1) x + 2 m - 1.$ Tìm tất cả các giá trị của để ba đường thẳng đồng quy

$A . m = 1$

$B . m = - 3$

$C . m \in \{- 3; 1\}$

$D . m = 3$

Xem đáp án

Ta gọi A là điểm 3 đường thẳng đồng quy.

Nên A là nghiệm hệ $\{\begin{cases} y = 2 x + 1 \\ y = x + 2 \end{cases} \Leftrightarrow \{\begin{cases} x = 1 \\ y = 3 \end{cases}$ . Để 3 đường thẳng đồng quy thì

$\begin{array}{l} A \in d : y = (m^{2} + 1) x + 2 m - 1. \\ \Rightarrow 3 = (m^{2} + 1) .1 + 2 m - 1 \Leftrightarrow m^{2} + 2 m - 3 = 0 \Leftrightarrow \{\begin{cases} m = 1 \\ m = - 3 \end{cases} \end{array}$

Chọn đáp án C

Câu 19:

Phương trình $2 x + 3 y = 300$ có bao nhiêu nghiệm nguyên dương ?

$A .40$

$B .49$

$C .50$

$D .59$

Xem đáp án

$2 x + 3 y = 300$ . Ta thấy $3 y ⋮ 3, 300 ⋮ 3 \Rightarrow 2 x ⋮ 3 \Rightarrow x ⋮ 3$

Đặt $x = 3 n (n > 0)$ $\Rightarrow 2 x + 3 y = 300 \Leftrightarrow 6 n + 3 y = 300$

Vì là số nguyên dương nên $\Leftrightarrow y = \frac{(300 - 6 n)}{3} = 100 - 2 n$ $y > 0 \Rightarrow 100 - 2 n > 0 \Leftrightarrow n < 50$

$0 < n < 50 \Rightarrow n \in \{1; 2; 3; ......; 48; 49\}$ nên số nghiệm nguyên dương thỏa mãn phương trình là : $(49 - 1) : 1 + 1 = 49$ nghiệm

Chọn đáp án B

Câu 20:

Cho hệ phương trình $\{\begin{cases} |x + 1| + y = 2 \\ x + 2 y = k \end{cases} .$ Tìm tất cả các giá trị của k để hệ phương trình đã cho có nghiệm duy nhất.

$A . k = 1$

$B . k = 2$

$C . k = 3$

$D . k = 4$

Xem đáp án

$\begin{array}{l} \{\begin{cases} |x + 1| + y = 2 \\ x + 2 y = k \end{cases} \\ +) x + 1 \geq 0 \Leftrightarrow x \geq - 1 \Rightarrow \{\begin{cases} x + 1 + y = 2 \\ x + 2 y = k \end{cases} \Rightarrow \{\begin{cases} x = 2 - k \\ y = k - 1 \end{cases} \\ x \geq 1 \Rightarrow 2 - k \geq - 1 \Rightarrow k \leq 3 \end{array}$

$\begin{array}{l} +) x + 1 < 0 \Rightarrow x < - 1 \Rightarrow \{\begin{cases} - x - 1 + y = 2 \\ x + 2 y = k \end{cases} \Leftrightarrow \{\begin{cases} x = \frac{1}{3} k - 2 \\ y = \frac{1}{3} k + 1 \end{cases} \\ x < - 1 \Rightarrow \frac{1}{3} k - 2 < - 1 \Leftrightarrow k < 3 \end{array}$

Hệ phương trình có nghiệm duy nhất $\Leftrightarrow k = 3 \Leftrightarrow \{\begin{cases} x = - 1 \\ y = 2 \end{cases}$

Chọn đáp án C

Câu 21:

Ba bình có dung tích tổng cộng là 120 lít. Nếu đổ đầy nước vào bình thứ nhất rồi lấy bình thứ nhất rót vào hai bình kia thì hoặc bình thứ ba đầy nước còn bình thứ hai chỉ được nửa thể tích của nó, hoặc bình thứ hai đầy nước còn bình thứ ba chỉ được một phần ba thể tích của nó. Thể tích bình lần lượt là :

$A .50 l, 40 l, 30 l$

$B .30 l, 40 l, 50 l$

$C .20 l, 30 l, 40 l$

$D .40 l, 30 l, 20 l$

Xem đáp án

Gọi $x, y$ lần lượt là thể tích bình thứ nhất và thứ hai với $0 < x, y < 120$ , ta lập được hệ phương trình :

$\{\begin{cases} x = \frac{1}{2} y + 120 - x - y \\ x = y + \frac{1}{3} (120 - x - y) \end{cases} \Leftrightarrow \{\begin{cases} x = 50 \\ y = 40 \end{cases}$

Thể tích mỗi bình lần lượt là $50 l, 40 l, 30 l$ Chọn đáp án A

Câu 22:

Một ô tô đi từ Hà Nội và dự định đến Huế lúc 12h trưa. Nếu xe đi với vận tốc $50 k m / h$ thì sẽ đến Huế chậm hơn dự định là 2 giờ. Nếu xe chạy với vận tốc $90 k m / h$ thì sẽ đến Huế sớm hơn dự định 2 giờ. Tính độ dài quãng đường từ Hà Nội đến Huế và thời điểm xuất phát

$A . 460 k m, 4 h s á n g$

$B . 400 k m, 5 h s á n g$

$C . 400 k m, 4 h s á n g$

$D .450 k m, 5 h s á n g$

Xem đáp án

Goi $x (k m)$ là độ dài quãng đường, $y$ (giờ) là thời gian dự định. Ta có:

$\{\begin{cases} 50 (y + 2) = x \\ 90 (y - 2) = x \end{cases} \Leftrightarrow \{\begin{cases} y = 7 \\ x = 450 \end{cases}$

Chọn đáp án D

Câu 23:

Phương trình $a x^{2} + b x + c = 0$ có nghiệm duy nhất khi và chỉ khi :

$A . a = 0$

$B . \{\begin{cases} a \neq 0 \\ Δ = 0 \end{cases} h o a c \{\begin{cases} a = 0 \\ b \neq 0 \end{cases}$

$C . a = b = 0$

$D . \{\begin{cases} a \neq 0 \\ Δ = 0 \end{cases}$

Xem đáp án

Phương trình $a x^{2} + b x + c = 0$ có nghiệm duy nhất khi và chỉ khi $\{\begin{cases} a \neq 0 \\ Δ = 0 \end{cases}$

Chọn đáp án B

Câu 24:

Phương trình $(m - 1) x^{2} + 3 x - 1 = 0.$ Phương trình có nghiệm khi :

$A . m \geq - \frac{5}{4}$

$B . m \leq - \frac{5}{4}$

$C . m = - \frac{5}{4}$

$D . m = \frac{5}{4}$

Xem đáp án

$(m - 1) x^{2} + 3 x - 1 = 0. Δ = 3^{2} + 4 (m - 1) .1 = 5 + 4 m$

Phương trình có nghiệm khi $Δ \geq 0 \Leftrightarrow 5 + 4 m \geq 0 \Leftrightarrow m \geq - \frac{5}{4}$

Chọn đáp án A

Câu 25:

Tìm số nguyên k nhỏ nhất sao cho phương trình : $2 (k x - 4) - x^{2} + 6 = 0$ vô nghiệm

$A . k = - 1$

$B . k = 1$

$C . k = 2$

$D . k = - 3$

Xem đáp án

$2 (k x - 4) - x^{2} + 6 = 0 \Leftrightarrow x^{2} - 2 k x + 2 = 0$

$Δ' = k^{2} - 2$

Để phương trình trên vô nghiệm thì $Δ' < 0 \Leftrightarrow k^{2} - 2 < 0 \Leftrightarrow - \sqrt{2} < k < \sqrt{2}$

Chọn đáp án B

Câu 26:

Cho phương trình $(x - 1) (x^{2} - 4 m x - 4) = 0.$ Phương trình có ba nghiệm phân biệt khi :

$A . m \in ℝ$

$B . m \neq 0$

$C . m \neq \frac{3}{4}$

$D . m \neq - \frac{3}{4}$

Xem đáp án

phương trình $(x - 1) (x^{2} - 4 m x - 4) = 0.$

$\Leftrightarrow [\begin{array}{l} x = 1 \\ x^{2} - 4 m x - 4 = 0 (*) \end{array}$

Để phương trình đề có 3 nghiệm thì phương trình (*) có 2 nghiệm phân biệt

$\Leftrightarrow Δ' > 0 \Leftrightarrow 4 m^{2} + 4 > 0$ (luôn đúng)

Và pt (*) có nghiệm khác 1 $\Leftrightarrow 1^{2} - 4 m - 4 \neq 0 \Leftrightarrow m \neq \frac{- 3}{4}$

Chọn đáp án D

Câu 27:

Điều kiện cần và đủ để phương trình

a x^{2} + b x + c = 0 (a \neq 0)

có hai nghiệm phân biệt cùng dấu khi :

$A . \{\begin{cases} Δ > 0 \\ P > 0 \end{cases}$

$B . \{\begin{cases} Δ \geq 0 \\ P > 0 \end{cases}$

$C . \{\begin{cases} Δ > 0 \\ S > 0 \end{cases}$

$D . \{\begin{cases} Δ > 0 \\ S < 0 \end{cases}$

Xem đáp án

Chọn đáp án A

Câu 28:

Điều kiện cần và đủ để phương trình $x^{2} - 4 x + 1 - m = 0,$ với giá trị nào của m thì phương trình có hai nghiệm thỏa mãn hệ thức $5 (x_{1} + x_{2}) - 4 x_{1} x_{2} = 0$

$A . m = 4$

$B . m = - 5$

$C . m = - 4$

$D . K h ô n g c ó m t h ỏ a m ã n$

Xem đáp án

$x^{2} - 4 x + 1 - m = 0$ có $Δ = 2^{2} - (1 - m) = m + 3$

Để phương trình đề có nghiệm $\Leftrightarrow m + 3 \geq 0 \Leftrightarrow m \geq - 3$ . Lúc đó, áp dụng Vi-et

$\Rightarrow \{\begin{cases} x_{1} + x_{2} = 4 \\ x_{1} x_{2} = 1 - m \end{cases}$

$5 (x_{1} + x_{2}) - 4 x_{1} x_{2} = 0 \Leftrightarrow 5.4 - 4 (1 - m) = 0 \Leftrightarrow m = - 4 (k t m)$

Vậy không có m thỏa mãn. Chọn đáp án D

Câu 29:

Với giá trị nào của m thì phương trình $x^{2} - 2 x + 3 m - 1 = 0$ có nghiệm $x_{1}, x_{2}$ thỏa mãn $x_{1}^{2} + x_{2}^{2} = 10 ?$

$A . m = - \frac{1}{3}$

$B . m = \frac{4}{3}$

$C . m = - \frac{2}{3}$

$D . m = \frac{2}{3}$

Xem đáp án

$x^{2} - 2 x + 3 m - 1 = 0$ có $Δ = {(- 1)}^{2} - (3 m - 1) = - 3 m$

Phương trình có nghiệm $\Leftrightarrow Δ' \geq 0 \Leftrightarrow - 3 m \geq 0 \Leftrightarrow m \leq 0$

Lúc đó, áp dụng $V i - e t \Rightarrow \{\begin{cases} x_{1} + x_{2} = 2 \\ x_{1} x_{2} = 3 m - 1 \end{cases}$

$x_{1}^{2} + x_{2}^{2} = 10 \Leftrightarrow {(x_{1} + x_{2})}^{2} - 2 x_{1} x_{2} = 10$

$\Leftrightarrow 2^{2} - 2 (3 m - 1) = 10 \Leftrightarrow 3 m - 1 = - 3 \Leftrightarrow m = \frac{- 2}{3} (t m)$

Chọn đáp án C

Câu 30:

Tìm tất cả các giá trị của m để phương trình $x^{2} - 2 (m + 1) x + m - 1 = 0$ có hai nghiệm $x_{1}, x_{2}$ và $x_{1}^{2} + x_{2}^{2} - 3 x_{1} x_{2}$ đạt giá trị nhỏ nhất ?

$A . m = - \frac{3}{8}$

$B . m = \frac{3}{8}$

$C . m = \frac{3}{2}$

$D . m = - \frac{3}{2}$

Xem đáp án

$x^{2} - 2 (m + 1) x + m - 1 = 0$ có

$Δ' = {(m + 1)}^{2} - (m - 1) = m^{2} + m + 2 > 0$ nên phương trình luôn có 2 nghiệm phân biệt $\Rightarrow \{\begin{cases} x_{1} + x_{2} = 2 m + 2 \\ x_{1} x_{2} = m - 1 \end{cases}$

$\begin{array}{l} x_{1}^{2} + x_{2}^{2} - 3 x_{1} x_{2} = {(x_{1} + x_{2})}^{2} - 5 x_{1} x_{2} \\ = {(2 m + 2)}^{2} - 5 (m - 1) = 4 m^{2} + 3 m + 9 \\ = {(2 m)}^{2} + 2.2 m . \frac{3}{4} + \frac{9}{16} + \frac{135}{16} \\ = {(2 m + \frac{3}{4})}^{2} + \frac{135}{16} \geq \frac{135}{16} \Leftrightarrow 2 m + \frac{3}{4} = 0 \Leftrightarrow m = \frac{- 3}{8} \end{array}$

Chọn đáp án A

Câu 31:

Tìm tất cả các giá trị của m để Parabol $(P) : y = \frac{1}{2} x^{2}$ cắt đường thẳng $(d) : y = m x + 1$ tại hai điểm phân biệt $A, B$ sao cho diện tích tam giác $O A B$ bằng $\sqrt{3}$

$A . m = 1$

$B . m = - 1$

$C . m = \sqrt{3}$

$D . m = \pm 1$

Xem đáp án

Chọn đáp án A

Câu 32:

Tìm tất cả giá trị của tham số m để đường thẳng

(D) : y = 2 m x - m^{2} + m - 2

tiếp xúc với Parabol

(P) : y = x^{2}

$A . m = 1$

$B . m = 2$

$C . m = - 2$

$D . m = 0$

Xem đáp án

ta có phương trình hoành độ giao điểm : $x^{2} - 2 m x + m^{2} - m + 2 = 0$

$Δ' = m^{2} - (m^{2} - m + 2) = m - 2$

Hai đồ thị tiếp xúc nhau khi $Δ' = 0 \Leftrightarrow m - 2 = 0 \Leftrightarrow m = 2$

Chọn đáp án B

Câu 33:

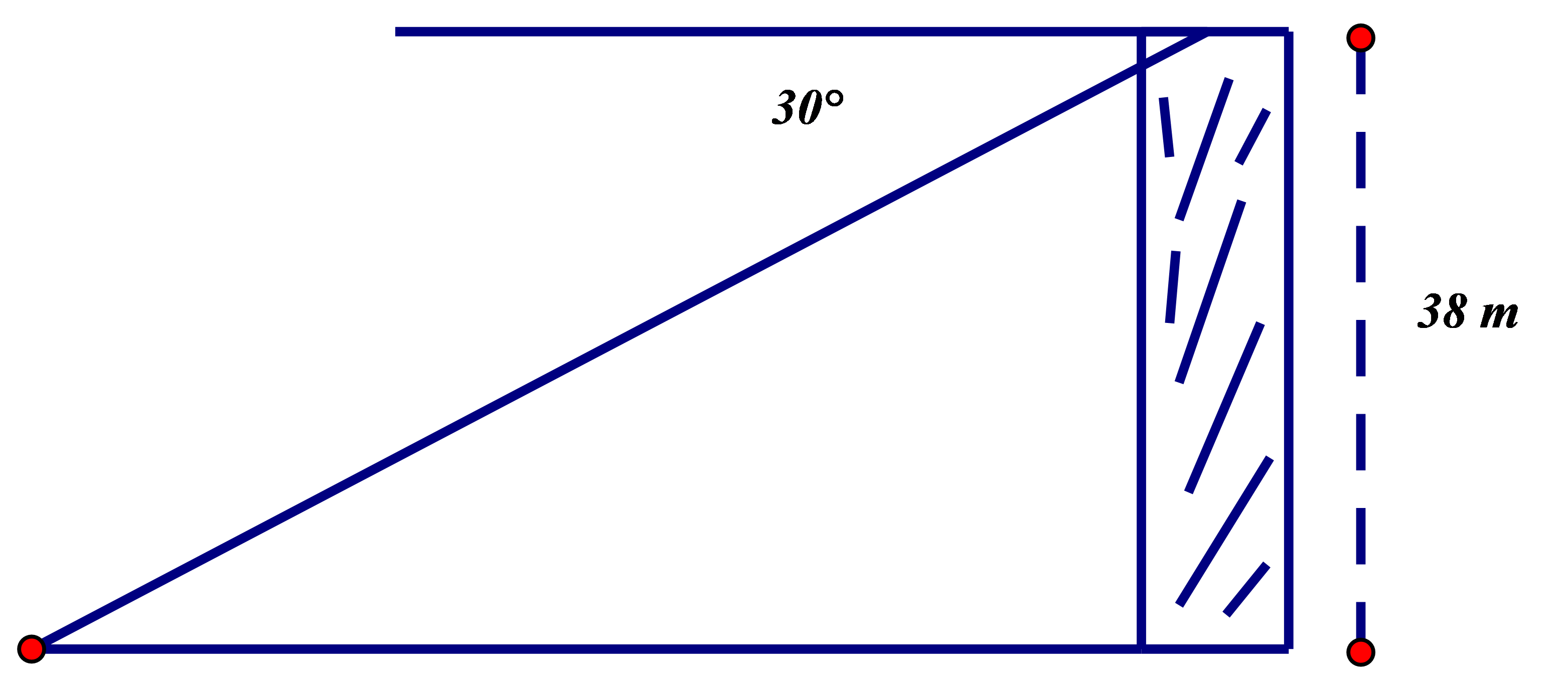
Từ một ngọn đèn biển cao 38m so với mực nước biển, người ta nhìn thấy một hòn đảo dưới góc $30^{0}$ so với đường nằm ngang chân đèn (hình trên). Tính khoảng cách từ đảo đến chân đèn (làm tròn đến hàng phần nghìn)

$A .65, 817 m$

$B .65, 82 m$

$C .65, 819 m$

$D .65, 818 m$

Xem đáp án

$d = 38. \cot 30 ° = 65, 818 m$

Chọn đáp án D

Câu 34:

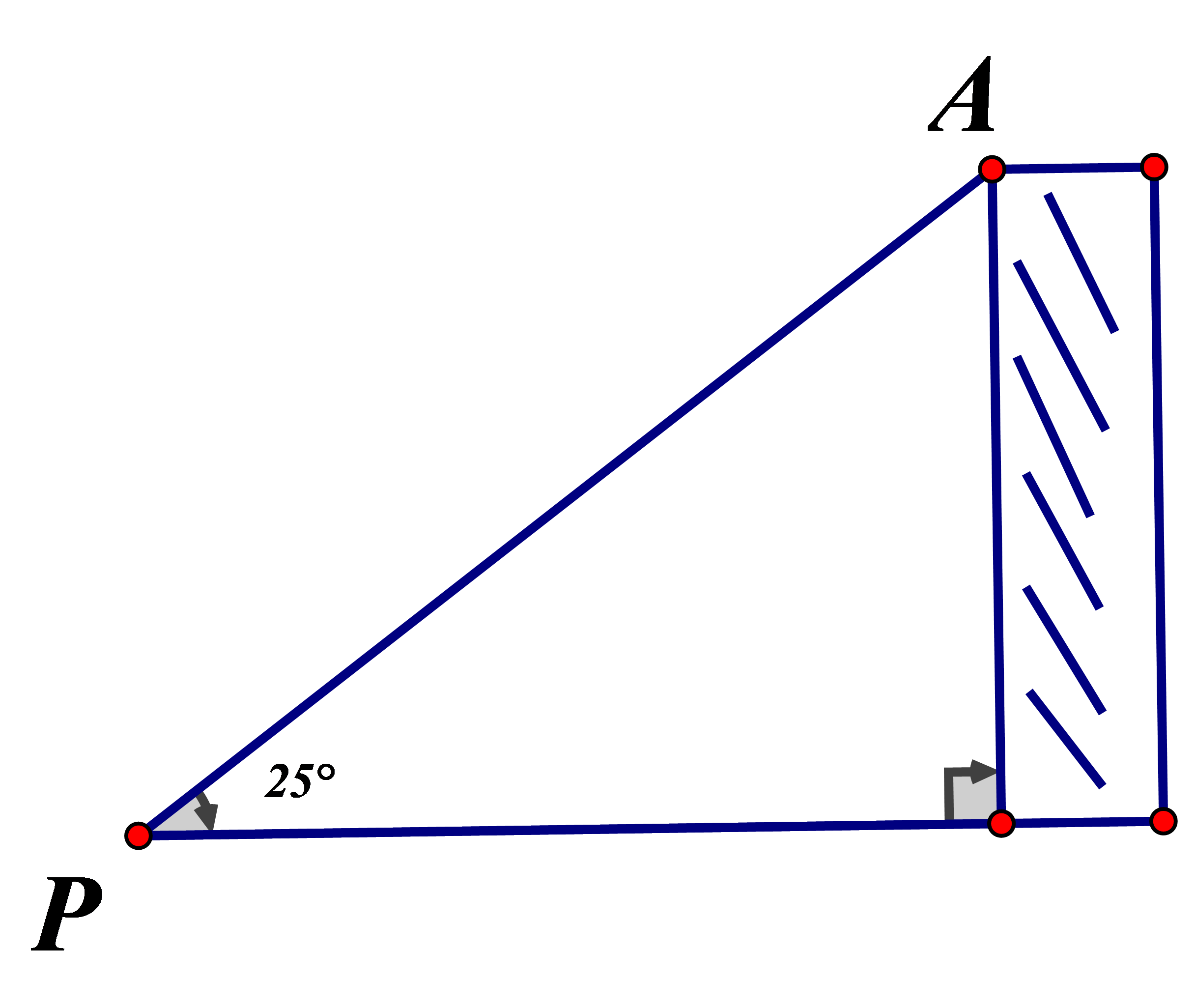
Để nhìn thấy đỉnh của một vách đá dựng đứng, người ta đã đứng tại điểm P cách chân vách đá một khoảng 45m và nhìn lên một góc $25^{0}$ so với đường nằm ngang (hình bên). Hãy tính độ cao của vách đá (làm tròn đến hàng phần nghìn)

$A .20, 984 m$

$B .20, 983 m$

$C .20, 985 m$

$D .20, 98 m$

Xem đáp án

$h = 45. \tan 25 ° \approx 20, 984 m$

Chọn đáp án A

Câu 35:

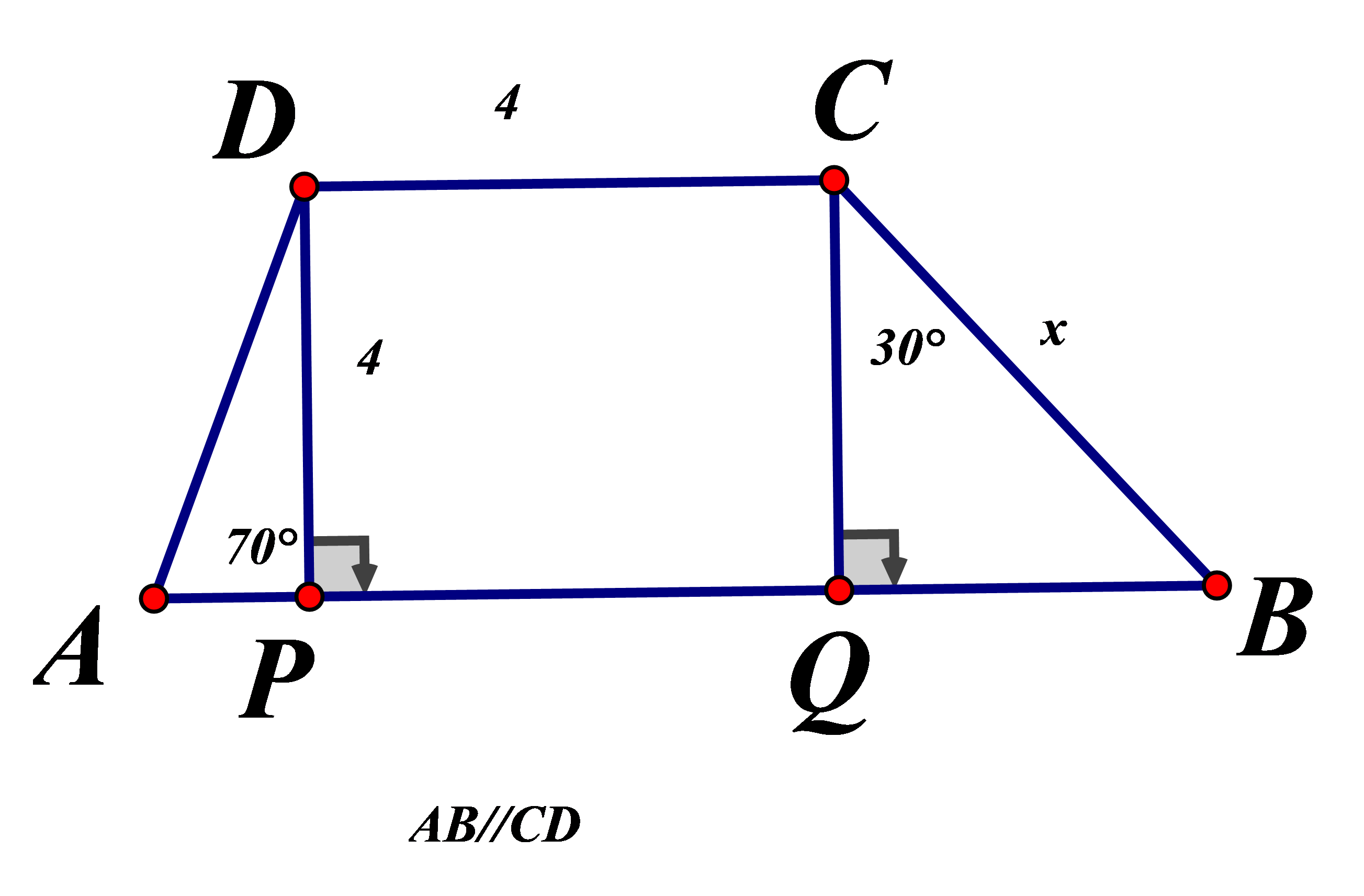
Tính x,y trong hình dưới (làm tròn đến hàng phần trăm )

Media VietJack

$\begin{array}{l} x = B C \\ y = A B \\ ∠ Q C B = 50 ° \end{array}$

$A . x = 6, 223, y = 10, 223$

$B . x = 6, 24, y = 10, 24$

$C . x = 6, 22, y = 10, 22$

$D . x = 6, 2, y = 10, 2$

Xem đáp án

Ta chứng minh được : $D C Q P$ là hình vuông $\Rightarrow C Q = 4$

$\begin{array}{l} \Rightarrow x = B C = \frac{C Q}{\cos 50 °} = 6, 22 (c m) \\ Q B = C Q . \tan 50 ° = 4, 767 c m \\ A P = \frac{4}{\tan 70 °} \approx 1, 456 c m \Rightarrow y = 1, 456 + 4 + 4, 767 = 10, 22 c m \end{array}$

Chọn đáp án C

Câu 36:

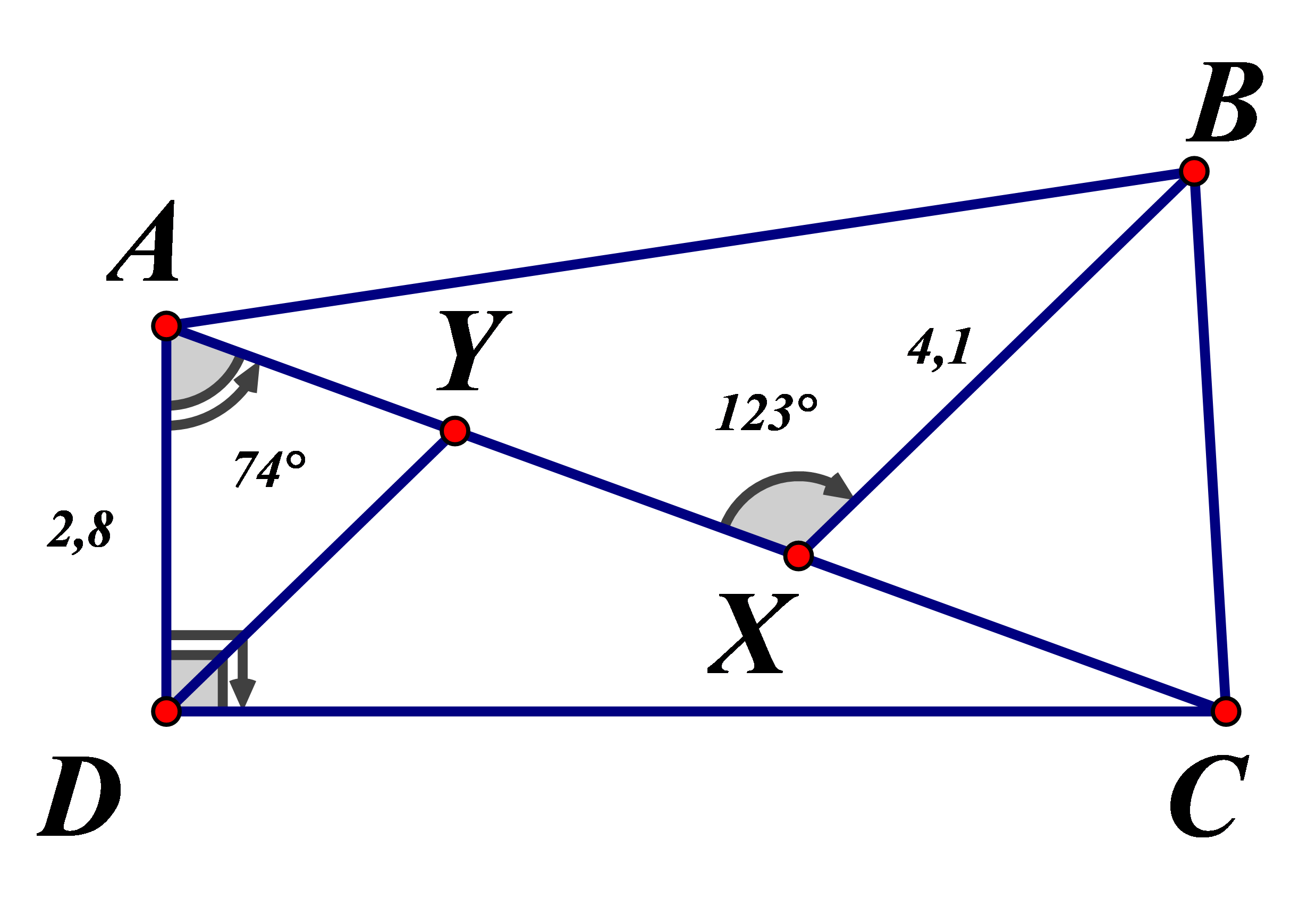
Cho hình bên, biết $A D ⊥ D C, ∠ D A C = 74^{0}, ∠ A X B = 123^{0}$ $, A D = 2, 8 c m, A X = 5, 5 c m, B X = 4, 1 (c m)$ . Gọi Y là điểm trên AX sao cho $D Y / / B X$ . Tính $A C, X Y$ và diện tích tam giác $B C X$ (làm tròn đến hàng phần nghìn).

$\begin{array}{l} A . A C \approx 10, 161 (c m), X Y \approx 2, 980 (c m), S_{B C X} \approx 8, 012 (c m^{2}) \end{array}$

$B . A C \approx 10, 160 (c m), X Y \approx 2, 980 (c m), S_{B C X} \approx 8, 012 (c m^{2})$

$C . A C \approx 10, 160 (c m), X Y \approx 2, 980 (c m), S_{B C X} \approx 8, 011 (c m^{2})$

$D . A C \approx 10, 160 (c m), X Y \approx 2, 981 (c m), S_{B C X} \approx 8, 012 (c m^{2})$

Xem đáp án

$Δ A D C$ vuông tại $D \Rightarrow A C = \frac{A D}{\cos ∠ D A C} = \frac{2, 8}{\cos 74 °} \approx 10, 158 c m$

Kẻ $A H ⊥ D Y$ tại H

$D Y / / B X \Rightarrow ∠ D Y X = ∠ B X Y = 123 °$ (so le trong)

Mà $∠ A Y D + ∠ D Y X = 180 ° \Rightarrow ∠ A Y D + 123 ° = 180 ° \Rightarrow ∠ A Y D = 57 °$

$Δ A D Y$ có : $∠ A D Y = 180 ° - ∠ D A Y - ∠ A Y D = 180 ° - 74 ° - 57 ° = 49 °$

$Δ A D H$ vuông tại H có : $A H = A D . \sin ∠ A D H = 2, 8. \sin 49 ° \approx 2, 11 c m$

$Δ A H Y$ vuông tại có: $A Y = \frac{A H}{\sin ∠ A Y H} \approx \frac{2, 11}{\sin 57 °} \approx 2, 52 (c m)$

$\Rightarrow X Y = A X - A Y = 5, 5 - 2, 52 \approx 2, 98 c m$

Kẻ $B K ⊥ A C$ tại K

Có $∠ B X K = 180 ° - ∠ B X A = 180 ° - 123 ° = 57 °$

$Δ B X K$ vuông tại có: $B K = B X . \sin ∠ B X K = 4, 1. \sin 57 ° = 3, 44 c m$

$\Rightarrow S_{B C K} = \frac{1}{2} B K . C X = \frac{1}{2} .3, 44.4, 7 \approx 8, 084 (c m^{2})$

Chọn đáp án D

Câu 37:

Cho tam giác ABC cân tại A, nội tiếp đường tròn (O) Đường cao AH cắt đường tròn ở D Tính số đo góc $∠ A C D$

$A {.45}^{0}$

$B {.60}^{0}$

$C {.90}^{0}$

$D {.30}^{0}$

Xem đáp án

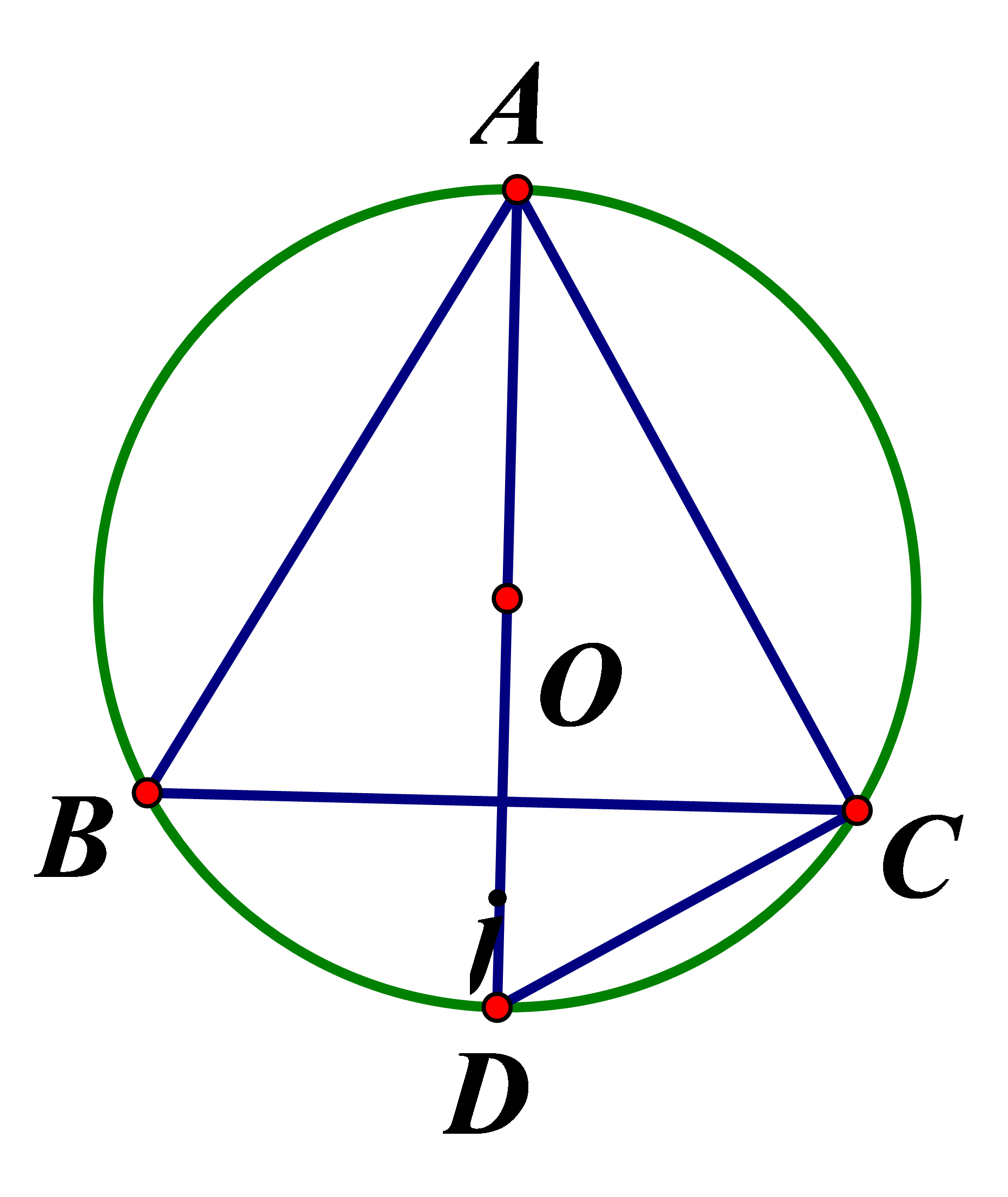
Vì $Δ A B C$ cân tại A nên AD đi qua O

Ta có $∠ A C D = 90 °$ (góc nội tiếp chắn nửa đường tròn)

Chọn đáp án C

Câu 38:

Tam giác ABC cân tại A, $B C = 12 c m,$ đường cao AH Tính bán kính của đường tròn ngoại tiếp tam giác $A B C$

$A .13 c m$

$B .6, 5 c m$

$C .6, 5$

$D .13$

Xem đáp án

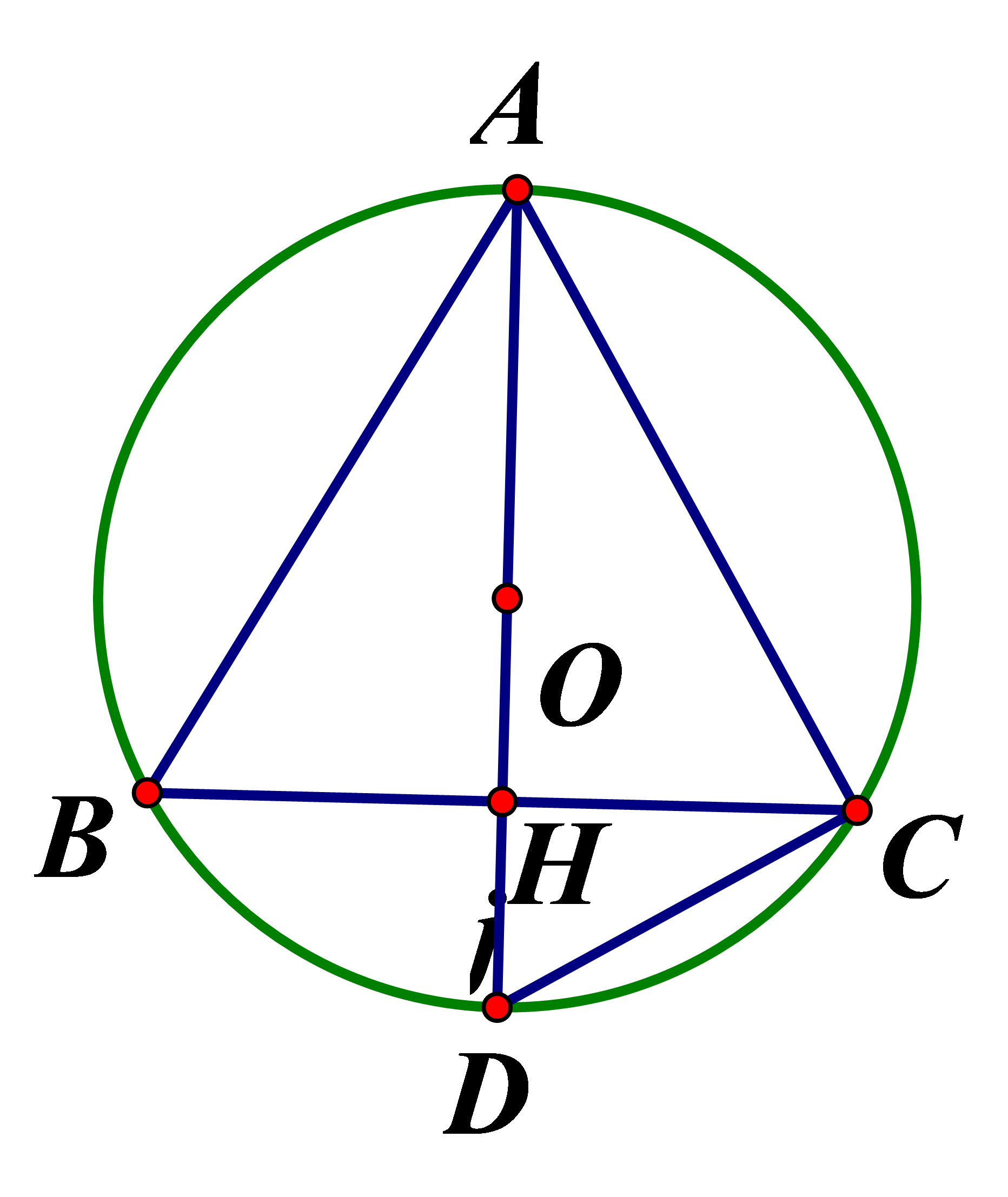
Vì $Δ A B C$ nội tiếp (O) $\Rightarrow A D$ là đường kính nên $Δ B C D$ vuông tại D

$\Rightarrow B H = \frac{B C}{2} = 6 c m$

$Δ B A D$ vuông tại $B, B H$ đường cao

$\begin{array}{l} \Rightarrow B H^{2} = A H . D H \Rightarrow D H = \frac{B H^{2}}{A H} = \frac{6^{2}}{4} = 9 c m \\ \Rightarrow A D = A H + D H = 4 + 9 = 13 c m \Rightarrow R = 6, 5 c m \end{array}$

Chọn đáp án C

Câu 39:

Cho đường tròn $(O; 2 c m)$ . Vẽ hai dây cung $A B, C D$ vuông góc với nhau. Tính diện tích lớn nhất của tứ giác $A B C D ?$

$A .32 c m^{2}$

$B .4 c m^{2}$

$C .16 c m^{2}$

$D .8 c m^{2}$

Xem đáp án

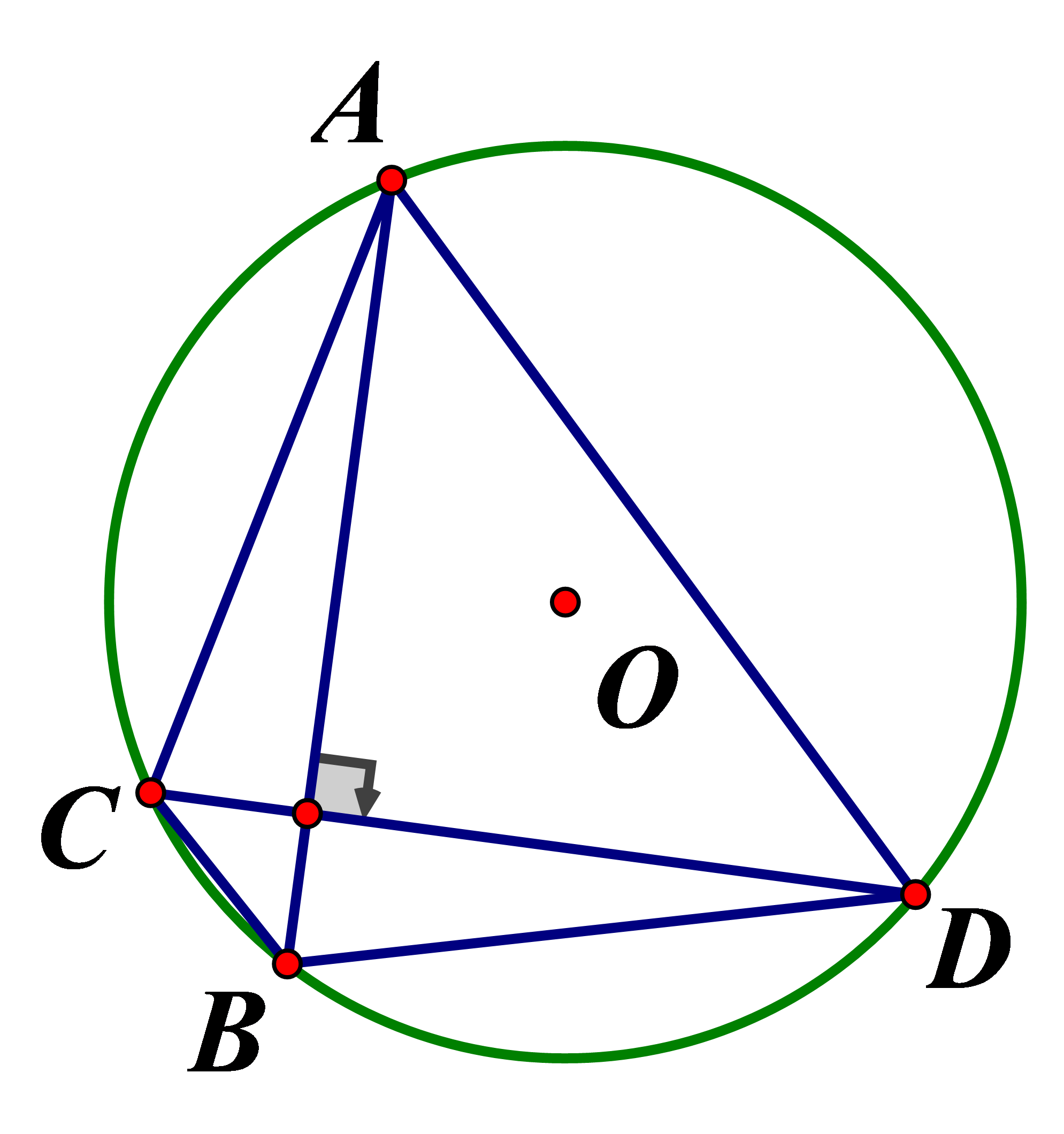
Ta có : $A B ⊥ C D \Rightarrow S_{A C B D} = \frac{A B . C D}{2}$

Lại có : $A B \leq 2 R = 4 c m, C D \leq 2 R = 4 c m \Rightarrow S_{A C D B \max} = \frac{4.4}{2} = 8 c m^{2}$

Chọn đáp án D

Câu 40:

Trong các câu sau, câu nào sai ?

$A . H a i đ ư ờ n g t r ò n t i ế p x ú c n g o à i t ạ i t h ì A t h u ộ c đ o ạ n t h ẳ n g n ố i t â m$

$B . H a i đ ư ờ n g t r ò n t i ế p x ú c t r o n g t ạ i A t h ì A t h u ộ c đ o ạ n n ố i t â m$

$C . N ế u h a i đ ư ờ n g t r ò n v à k h ô n g g i a o n h a u t h ì$

$D . N ế u h a i đ ư ờ n g t r ò n v à t i ế p x ú c t r o n g t h ì$

Xem đáp án

Chọn đáp án D

Câu 41:

Tính bán kính đường tròn tiếp xúc với tất cả các cạnh của hình vuông ABCD biết $A B = 2 (c m)$

$A .1 c m$

$B .2 c m$

$C . \sqrt{2} c m$

$D . \frac{\sqrt{2}}{2} c m$

Xem đáp án

$R = O A = \frac{A B}{2} = 1 c m$

Chọn đáp án A

Câu 42:

Cho tứ giác ABCD nội tiếp và $∠ B A C = 40^{0} .$ Tính số đo _{$∠ B D C$}

$A {.60}^{0}$

$B {.40}^{0}$

$C {.140}^{0}$

$D {.320}^{0}$

Xem đáp án

Vì là tứ giác ABCD nội tiếp nên

$∠ B D C = 180 ° - ∠ B A C = 180 ° - 40 ° = 140 °$ . Chọn đáp án C

Câu 43:

Cho hai điểm A,B cố định và góc $α$ không đổi $(0^{0} < α < 180^{0}) . M$ là điểm thay đổi sao cho $∠ A M B = α .$ Khi đó $M$ di động trên đường nào ?

$A . Đ ư ờ n g t r ò n đ ư ờ n g k í n h A B$

$B . Đ ư ờ n g t r u n g t r ự c c ủ a đ o ạ n A B$

$C . M ộ t c u n g t r ò n$

$D . H a i c u n g t r ò n .$

Xem đáp án

Chọn đáp án C

Câu 44:

Cho hình vuông $A B C D$ nội tiếp đường tròn tâm O, bán kính R.Điểm M bất kỳ thuộc cung nhỏ AD thì số đo của góc $∠ C M D$ bằng:

$A .22, 5^{0}$

$B {.45}^{0}$

$C {.90}^{0}$

$D . K h ô n g t í n h đ ư ợ c$

Xem đáp án

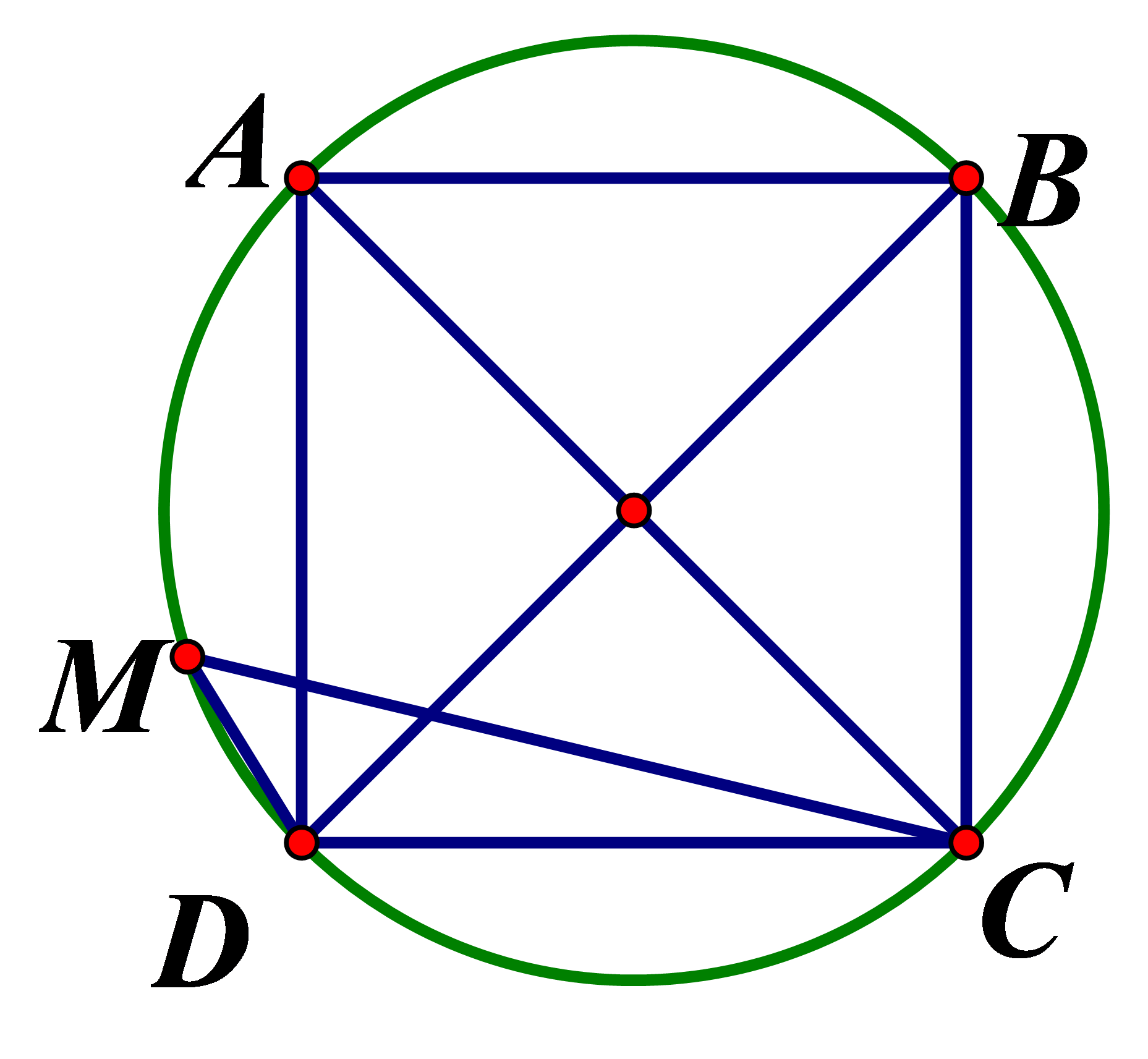
$∠ C D M = \frac{1}{2} s d \overset{⏜}{C M} = \frac{1}{2} (s d \overset{⏜}{C A} + s d \overset{⏜}{A M})$ mà không rõ số đo cung AM do M là điểm di động Chọn đáp án D

Câu 45:

Cho hình vẽ, biết $M T = 20 c m, M B = 50 c m .$ Tính bán kính đường tròn

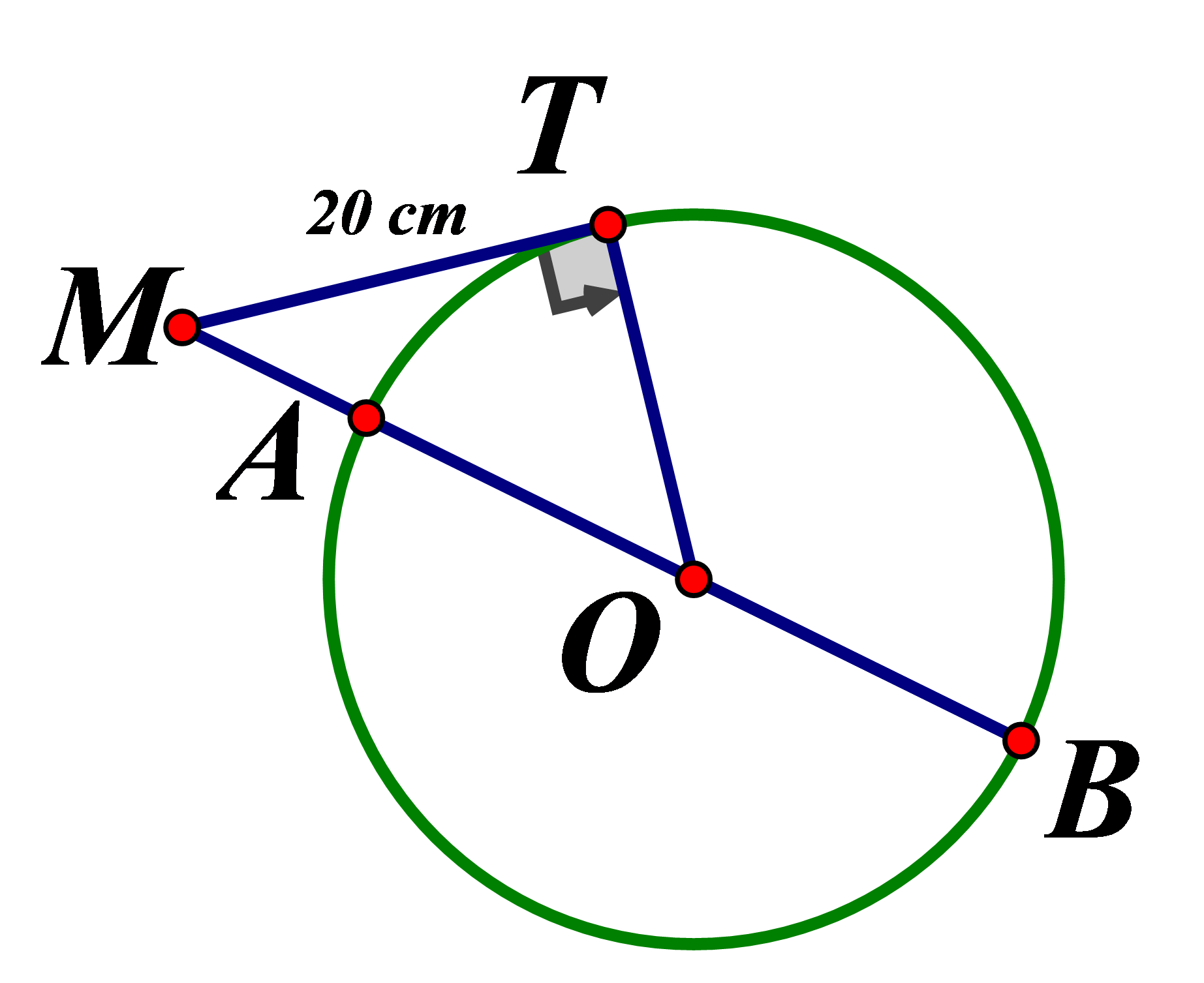
Media VietJack

$A .20$

$B .21$

$C .8$

$D .12$

Xem đáp án

Áp dụng phương tích trong đường tròn

$\begin{array}{l} \Rightarrow M T^{2} = M A . M B \Rightarrow M A = \frac{M T^{2}}{M B} = \frac{20^{2}}{50} = 8 \\ \Rightarrow R = \frac{A B}{2} = \frac{M B - M A}{2} = \frac{50 - 8}{2} = 21 c m \end{array}$

Chọn đáp án B

Câu 46:

Cho hình vẽ. Số đo

∠ B C D

bằng:

$A {.50}^{0}$

$B {.80}^{0}$

$C {.130}^{0}$

$D {.45}^{0}$

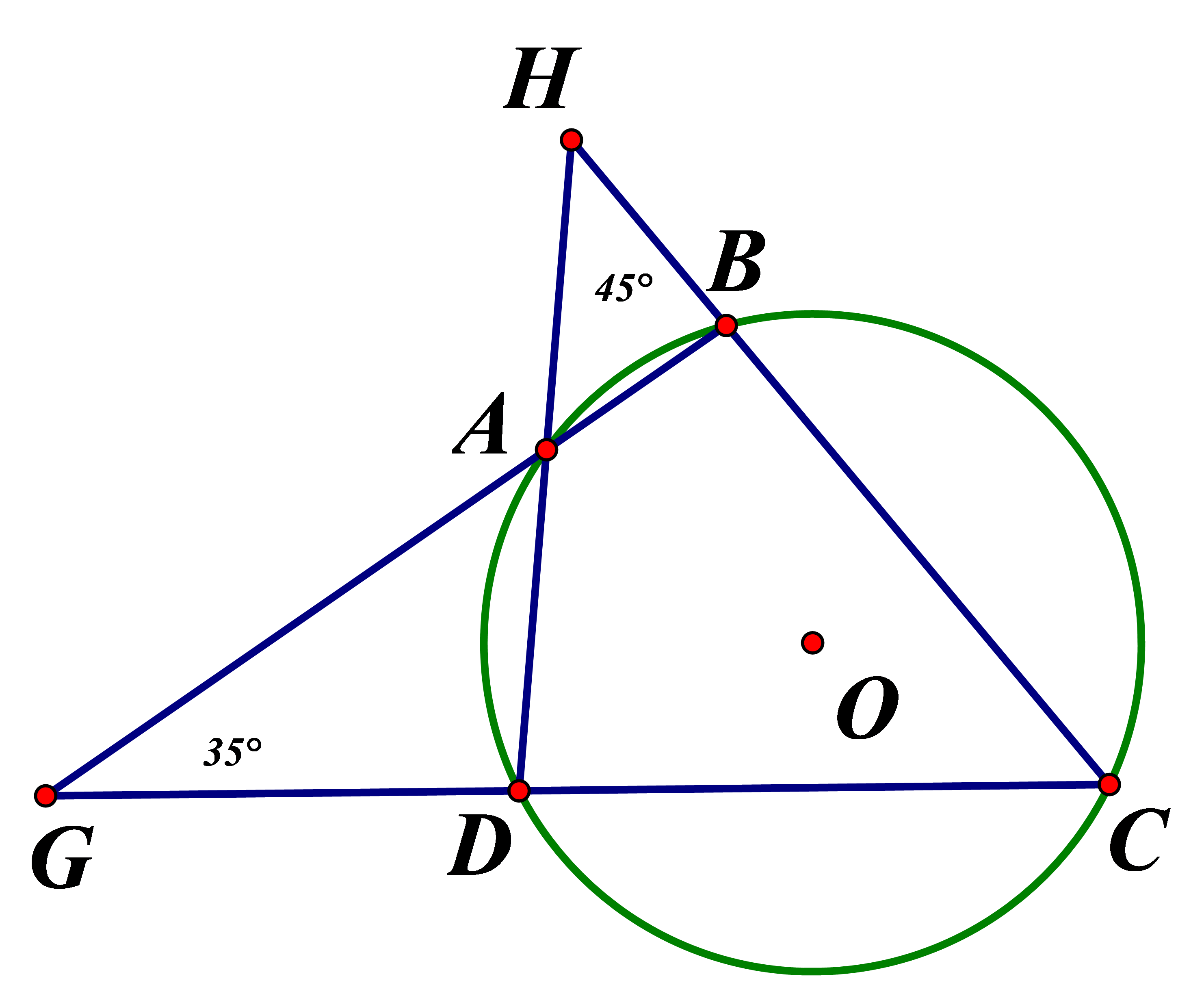
Xem đáp án

Áp dụng tính chất góc ngoài của tam giác

$\Rightarrow ∠ A B C = 45 ° + ∠ H A B; ∠ A D C = 35 ° + ∠ G A D$

$\Rightarrow ∠ A B C + ∠ A D C = 45 ° + 35 ° + 2 ∠ H A B$ (do $∠ H A B = ∠ G C D$ (đối đỉnh))

$\Rightarrow ∠ H A B = \frac{180 ° - (45 ° + 35 °)}{2} = 50 °$

Mà $A B C D$ là tứ giác nội tiếp nên $∠ B C D = ∠ H A B = 50 °$

Chọn đáp án A

Câu 47:

Tam giác ABC cân tại A nội tiếp đường tròn . Gọi I là tâm đường tròn nội tiếp tam giác. Các đường phân giác $∠ B, ∠ C$ của tam giác lần lượt cắt đường tròn (O) tại D và E. Tứ giác $A D I E$ là hình gì ?

$A . H ì n h t h a n g v à k h ô n g l à h ì n h b ì n h h à n h$

$B . H ì n h b ì n h h à n h v à k h ô n g l à h ì n h t h o$

$C . H ì n h t h o i v à k h ô n g l à h ì n h c h ữ n h ậ t$

$D . H ì n h c h ữ n h ậ t$

Xem đáp án

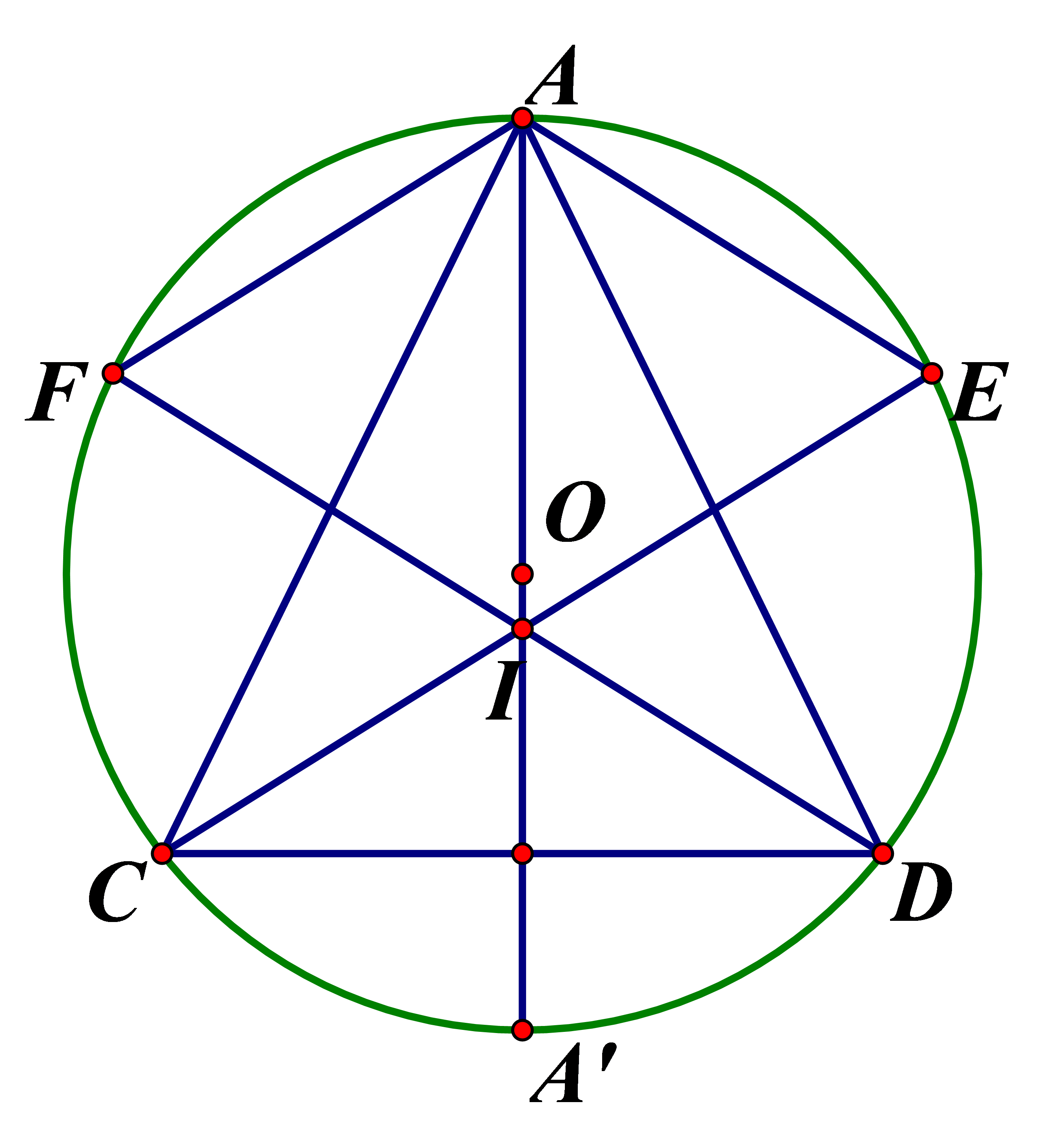
$∠ B = ∠ C$ và $B D, C E$ là hai tia phân giác nên

$∠ A B D = ∠ C B D = ∠ B C E = ∠ A C E \Rightarrow s d \overset{⏜}{B E} = s d \overset{⏜}{E A} = s d \overset{⏜}{A D} = s d \overset{⏜}{D C} (1)$

Gọi $A I \cap (O) = A' \Rightarrow A A'$ là đường kính $\Rightarrow s d \overset{⏜}{A' C} = s d \overset{⏜}{A' B}, s d \overset{⏜}{A' D} = s d \overset{⏜}{A' E} (2)$

Áp dụng góc nội tiếp và góc có đỉnh bên trong đường tròn ta có:

$\begin{array}{l} ∠ D A I = \frac{1}{2} s d \overset{⏜}{A' D} = \frac{1}{2} (s d A' C + s d \overset{⏜}{C D}) (3) \\ ∠ A I D = \frac{1}{2} s d (\overset{⏜}{A B} + s d \overset{⏜}{A' B}) (4) \end{array}$

Từ $(1), (2), (3), (4) \Rightarrow ∠ D A I = ∠ A I D \Rightarrow Δ A I D$ cân tại D

Chứng minh tương tự cân tại E $\Rightarrow A E = I E (b)$

Mà $s d \overset{⏜}{A E} = s d \overset{⏜}{A D} (c m t) \Rightarrow A E = A D (c)$

Từ (a), (b), (c), (d) $\Rightarrow A E = E I = I D = D A \Rightarrow A E I D$ là hình thoi

Chọn đáp án C

Câu 48:

Cho tam giác ABC nội tiếp đường tròn (O;R).Đường phân giác trong và ngoài của góc A cắt đường thẳng BC theo thứ tự tại D và E sao cho $A D = A E .$ Tính $A B^{2} + A C^{2} ?$

$A .4 R^{2}$

$B .2 R^{2}$

$C . R^{2}$

$D .3 R^{2}$

Xem đáp án

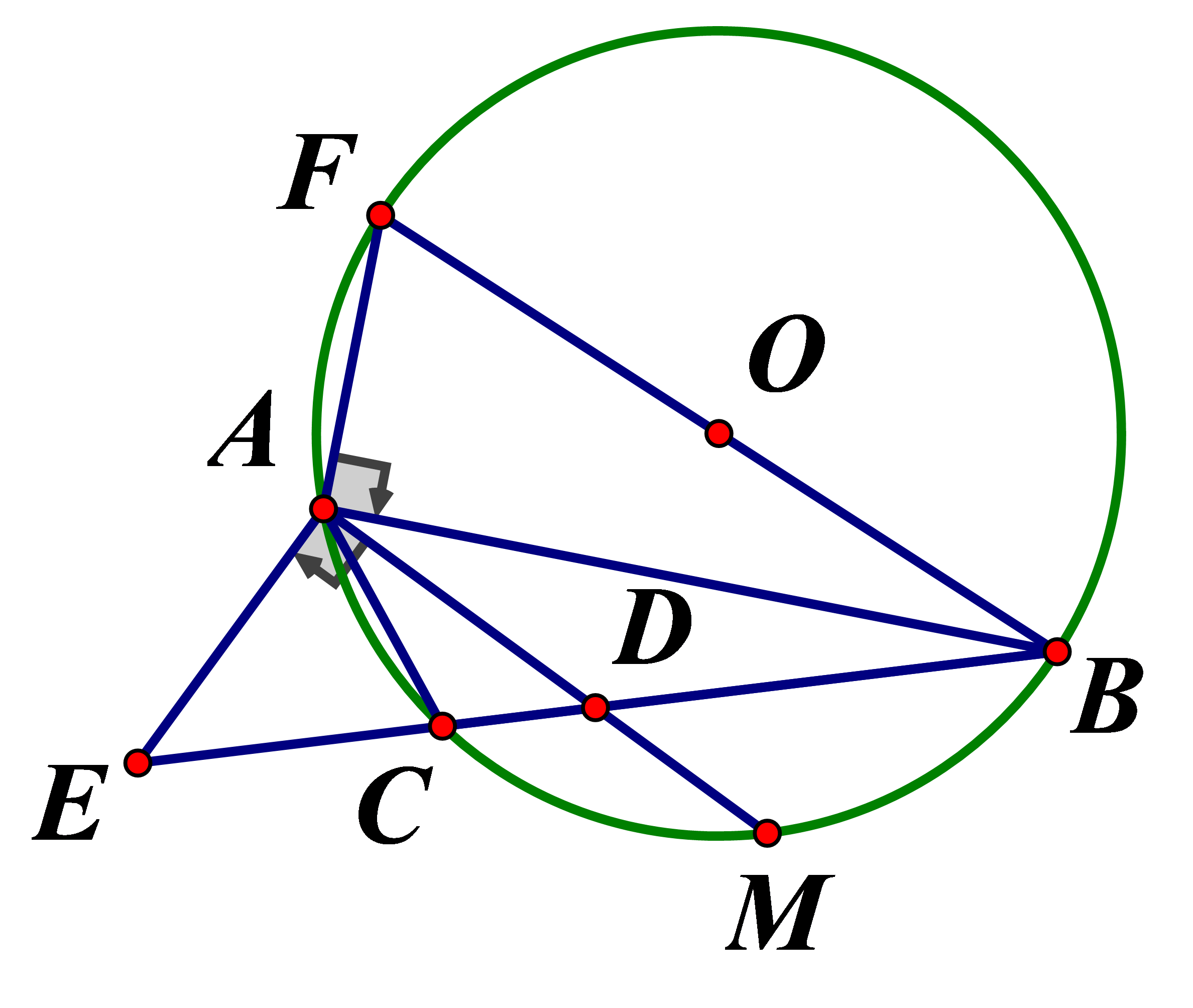
AD cắt đường tròn (O) tại M Kẻ đường kính BF

Ta có: $Δ A D E$ vuông cân tại A nên $∠ A D C = 45 ° \Rightarrow \frac{s d \overset{⏜}{B M} + s d \overset{⏜}{A C}}{2} = 45 °$

$\Rightarrow s d \overset{⏜}{B M} + s d \overset{⏜}{A C} = 90 °$ mà $\overset{⏜}{B M} = \overset{⏜}{M C} \Rightarrow \overset{⏜}{A F} = \overset{⏜}{A C} \Rightarrow A F = A C$

Do đó $A B^{2} + A C^{2} = A B^{2} + A F^{2} = B F^{2} = 4 R^{2}$

Chọn đáp án A

Câu 49:

Trong mặt phẳng, cho hai điểm A,B cố định phân biệt. Với điểm M thỏa mãn $∠ A M B = 90^{0}$ thì điểm M

$A . T h u ộ c m ộ t đ ư ờ n g c ó b á n k í n h b ằ n g A B$

$B . T h u ộ c m ộ t đ ư ờ n g t r ò n b á n k í n h b ằ n g 2 A B$

$C . T h u ộ c m ộ t đ ư ờ n g t r ò n b á n k í n h b ằ n g 3 A B$

$D . T h u ộ c m ộ t đ ư ờ n g t r ò n đ ư ờ n g k í n h b ằ n g A B$

Xem đáp án

Vì $∠ A M B = 90 °$ nên M thuộc đường tròn đường kính

Chọn đáp án D