50 câu hỏi trắc nghiệm thuộc Bộ 30 đề thi vào 10 môn Toán có lời giải chi tiết (Đề 10)

Câu 1:

Cho $Δ A B C$ có $∠ A = 90^{0}, A B = 6, A C = 8.$ Gọi M là trung điểm của $B C, G$ là trọng tâm của $Δ A B C$ . Tính $G M$

$A . G M = \frac{5}{2}$

$B . G M = \frac{5}{6}$

$C . G M = \frac{10}{3}$

$D . G M = \frac{5}{3}$

Xem đáp án

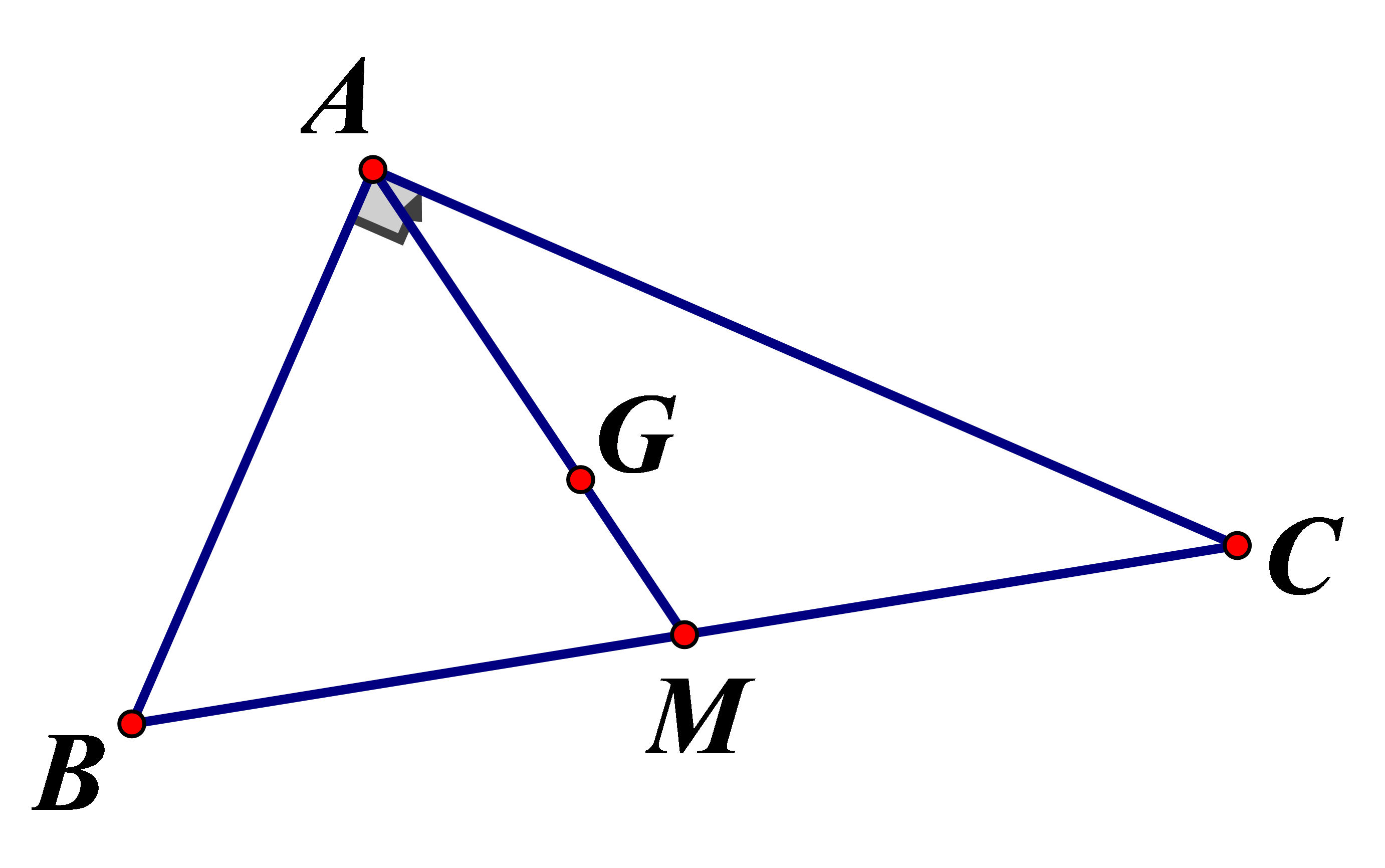
Áp dụng định lý Pytago trong tam giác vuông

$\Rightarrow B C = \sqrt{A B^{2} + A C^{2}} = \sqrt{6^{2} + 8^{2}} = 10 (c m)$

$\Rightarrow A M = \frac{1}{2} B C = 5 (c m) \Rightarrow G M = \frac{1}{3} A M = \frac{5}{3} (c m)$ (tính chất trọng tâm)

Chọn đáp án D

Câu 2:

Đẳng thức nào sau đây đúng với $x \leq 0 ?$

$A . \sqrt{4 x^{2}} = 2 x$

$B . \sqrt{4 x^{2}} = 4 x$

$C . \sqrt{4 x^{2}} = - 4 x$

$D . \sqrt{4 x^{2}} = - 2 x$

Xem đáp án

$\sqrt{4 x^{2}} = - 2 x k h i x \leq 0$

Chọn đáp án D

Câu 3:

Cho $Δ A B C$ vuông tại A.Biết $∠ B = 60^{0}, A C = 10 c m .$ Khẳng định nào sau đây đúng ?

$A . B C = 10 \sqrt{3} c m$

$B . B C = 20 \sqrt{3} c m$

$C . B C = 15 \sqrt{3} c m$

$D . B C = \frac{20 \sqrt{3}}{3} c m$

Xem đáp án

$B C = \frac{A C}{\sin 60 °} = \frac{10}{\frac{\sqrt{3}}{2}} = \frac{20 \sqrt{3}}{3} (c m)$

Chọn đáp án D

Câu 4:

Cho biểu thức $Q = |x - 3| + |x + 2|$ . Tính tổng T các số nguyên x khi Q đạt giá trị lớn nhất .

$A . T = 3$

$B . T = 7$

$C . T = 5$

$D . T = 9$

Xem đáp án

$Q_{\max} = 5 \Leftrightarrow \{\begin{cases} (x - 3) (x + 2) \geq 0 \\ (x - 3) (x + 2) \leq 0 \end{cases} \Leftrightarrow - 2 \leq x \leq 3 \Rightarrow x \in \{0; \pm 1; \pm 2; 3\} \Rightarrow S = 3$

Chọn đáp án A

Câu 5:

Tìm giá trị nhỏ nhất $y_{0}$ của hàm số $y = 2 x^{2}$

$A . y_{0} = 1$

$B . y_{0} = - 2$

$C . y_{0} = \frac{1}{2}$

$D . y_{0} = 0$

Xem đáp án

$y = 2 x^{2} \geq 0$ với mọi x nên $\min = y_{0} = 0 \Leftrightarrow x = 0$ . Chọn đáp án D

Câu 6:

Cho hàm số $y = 2 x - b .$ Xác định b nếu đồ thị hàm số đi qua điểm $M (1; - 2)$

$A . b = 4$

$B . b = - 4$

$C . b = 2$

$D . b = - 2$

Xem đáp án

Đồ thị hàm số $y = 2 x - b$ qua điểm $M (1; - 2)$

$\Rightarrow - 2 = 2.1 - b \Leftrightarrow b = 4$ .Chọn đáp án A

Câu 7:

Cho tam giác $M N P$ có $M N = 10, N P = 10, P M = 15.$ Khẳng định nào sau đây đúng ?

$A . ∠ M > ∠ P > ∠ N$

$B . ∠ M = ∠ P > ∠ N$

$C . ∠ M < ∠ P = ∠ N$

$D . ∠ M = ∠ P < ∠ N$

Xem đáp án

Áp dụng quan hệ giữa cạnh và góc ta có

$M N = 10, N P = 10, P M = 15. \Rightarrow ∠ P = ∠ M < ∠ N$ .Chọn đáp án D

Câu 8:

Hàm số nào sau đây luôn nghịch biến với mọi $x \in ℝ ?$

$A . y = - x^{2}$

$B . y = 1 - \frac{x}{3}$

$C . y = - 2 + x$

$D . y = - \frac{1}{2} x^{2}$

Xem đáp án

Hàm số $y = a x + b (a \neq 0)$ nghịch biến trên R khi $a < 0$ . Chọn đáp án B

Câu 9:

Tìm tổng S tất cả các giá trị của m để phương trình $3 x^{2} + (2 - m) x + m + 1 = 0$ có nghiệm kép ?

$A . S = - 16$

$B . S = 16$

$C . S = - 8$

$D . S = 8$

Xem đáp án

Để phương trình có nghiệm kép $\Leftrightarrow Δ = 0$

$\Leftrightarrow {(2 - m)}^{2} - 4.3. (m - 1) = 0 \Leftrightarrow m^{2} - 16 m + 16 = 0 \Leftrightarrow m = 8 \pm \sqrt{3}$

Nên tổng $m : 8 - 4 \sqrt{3} + 8 + 4 \sqrt{3} = 16$

Chọn đáp án B

Câu 10:

Điểm nào sau đây không thuộc đồ thị hàm số $y = 2 x - 3 ?$

$A . M (- 1; 4)$

$B . M (\frac{1}{2}; - 2)$

$C . Q (1; - 1)$

$D . N (0; - 3)$

Xem đáp án

Ta thay lần lượt các điểm vào đồ thị có $M (- 1; 4)$ không thỏa mãn

Chọn đáp án A

Câu 11:

Hai người thợ cùng làm một công việc trong 16 giờ thì xong. Nếu người thứ nhất làm 3 giờ và người thứ hai làm 6 giờ thì chỉ hoàn thành $25 %$ công việc. Hỏi nếu làm riêng thì người thứ nhất hoàn thành công việc đó trong bao lâu ?

$A . 48 g i ờ$

$B . 9 g i ờ$

$C . 24 g i ờ$

$D . 12 g i ờ$

Xem đáp án

Gọi x,y là số giờ cả hai người làm xong, theo bài ta có hệ :

$\{\begin{cases} \frac{1}{x} + \frac{1}{y} = \frac{1}{16} \\ \frac{3}{x} + \frac{6}{y} = \frac{1}{4} \end{cases} \Leftrightarrow \{\begin{cases} x = 24 \\ y = 48 \end{cases}$ . Vậy người thứ nhất làm 1 mình hết 24 giờ

Chọn đáp án C

Câu 12:

Cho $Δ A B C$ vuông tại A, đường cao AH Khẳng định nào sau đây đúng ?

$A . \sin C = \frac{A B}{A C}$

$B . \sin C = \frac{A B}{B C}$

$C . \sin C = \frac{A H}{B H}$

$D . \sin C = \frac{A H}{A B}$

Xem đáp án

$\sin C = \frac{A B}{B C}$

Chọn đáp án B

Câu 13:

Tính tổng S tất cả các nghiệm của phương trình

{(2 x^{2} + x - 4)}^{2} - 4 x^{2} + 4 x - 1 = 0

$A . S = - 1$

$B . S = - 2$

$C . S = 1$

$D . S = 2$

Xem đáp án

$\begin{array}{l} {(2 x^{2} + x - 4)}^{2} - 4 x^{2} + 4 x - 1 = 0 \Leftrightarrow {(2 x^{2} + x - 4)}^{2} = 4 x^{2} - 4 x + 1 \\ \Leftrightarrow {(2 x^{2} + x - 4)}^{2} = {(2 x - 1)}^{2} \Rightarrow [\begin{array}{l} 2 x^{2} + x - 4 = 2 x - 1 \\ 2 x^{2} + x - 4 = 1 - 2 x \end{array} \Leftrightarrow [\begin{array}{l} 2 x^{2} - x - 3 = 0 \\ 2 x^{2} + 3 x - 5 = 0 \end{array} \\ \Leftrightarrow [\begin{array}{l} x = \frac{3}{2}; x = - 1 \\ x = 1; x = \frac{- 5}{2} \end{array} \end{array}$

Nên $S = \frac{3}{2} - 1 + 1 - \frac{5}{2} = - 1$ .Chọn đáp án A

Câu 14:

Tâm đường tròn ngoại tiếp tam giác là trung điểm của cạnh lớn nhất nếu tam giác đó có :

$A . C ó g ó c t ù$

$B . C ó 3 g ó c n h ọ n$

$C . c ó g ó c v u ô n g$

$D . c ó h a i g ó c n h ọ n$

Xem đáp án

Tam giác có tâm đường tròn ngoại tiếp là trung điểm của cạnh lớn nhất là tam giác vuông. Chọn đáp án C

Câu 15:

Cặp số (1,0) là nghiệm của hệ phương trình nào dưới đây ?

$A . \{\begin{cases} 2 x + y = 3 \\ x - 2 y = 2 \end{cases}$

$B . \{\begin{cases} 2 x - y = 2 \\ 3 x + 2 y = 3 \end{cases}$

$C . \{\begin{cases} 2 x + y = 4 \\ 2 x - 3 y = 2 \end{cases}$

$D . \{\begin{cases} 2 x + y = 3 \\ x - y = 2 \end{cases}$

Xem đáp án

Cặp số $(1; 0)$ ta thay vào các hệ phương trình có $\{\begin{cases} 2 x - y = 2 \\ 3 x + 2 y = 3 \end{cases}$ thỏa mãn

Chọn đáp án B

Câu 16:

Một phân số có tử số bé hơn mẫu số là 5. Nếu tăng tử số lên 3 đơn vị và giảm mẫu số đi 6 đơn vị thì được một phân số bằng Tìm phân số ban đầu

$A . \frac{7}{12}$

$B . \frac{8}{15}$

$C . \frac{8}{13}$

$D . \frac{9}{14}$

Xem đáp án

Gọi phân số cần tìm có dạng $\frac{a}{a + 5} (a \neq - 5)$ . Theo bài ta có phương trình

$\frac{a + 3}{a + 5 - 6} = \frac{3}{2} \Rightarrow 2 a + 6 = 3 a - 1 \Leftrightarrow a = 7$ nên phân số cần tìm là

Chọn đáp án A

Câu 17:

Tính diện tích của hình tam giác giới hạn bởi các đường thẳng $y = - x + 6,$ $y = 2 x$ và trục Ox Biết rằng, mỗi đơn vị trên trục tọa độ có độ dài

$A . S = 36 c m^{2}$

$B . S = 24 c m^{2}$

$C . S = 18 c m^{2}$

$D . S = 12 c m^{2}$

Xem đáp án

Gọi $A, B, C$ là tọa độ của giao điểm của 2 đường thẳng và của mỗi đường thẳng với trục Ox $\Rightarrow A (2; 4), B (6; 0), C (0; 0)$

$\Rightarrow A B = 4 \sqrt{2}, A C = 2 \sqrt{5}, B C = 6$

Áp dụng định lý Hê rông với p là nửa chu vi ta có:

$S = \sqrt{p (p - A B) (p - A C) (p - B C)} = 12 (d v d t)$

Chọn đáp án D

Câu 18:

Số nghiệm của phương trình

|3 x - 2| = 2 - 3 x

bằng bao nhiêu ?

$A . V ô s ố n g h i ệ m$

$B . 2$

$C . 1$

$D . 0$

Xem đáp án

$|3 x - 2| = 2 - 3 x \Leftrightarrow [\begin{array}{l} 3 x - 2 = 2 - 3 x (x \geq \frac{2}{3}) \\ 2 - 3 x = 2 - 3 x (x \leq \frac{2}{3}) \end{array} \Leftrightarrow [\begin{array}{l} 6 x = 4 \Leftrightarrow x = \frac{2}{3} (t m) \\ x \in R / x \leq \frac{2}{3} \end{array} \Rightarrow x \leq \frac{2}{3}$

Chọn đáp án A

Câu 19:

Với cùng số tiền mua 36 quyển vở loại I có thể mua được bao nhiêu quyển vở loại II.Biết giá tiền quyển vở loại II bằng $75 %$ giá tiền một quyển vở loại I.

$A . 48 q u y ể n$

$B . 40 q u y ể n$

$D . 32 q u y ể n$

Xem đáp án

Số quyển vở loại II mua được : $36 : 75 % = 48$ (quyển)

Chọn đáp án A

Câu 20:

Số học sinh ba lớp $7 A, 7 B, 7 C$ của một trường tỉ lệ với $9; 8; 7.$ Số học sinh lớp $7 A$ nhiều hơn số học sinh lớp 7C là 10 em. Hỏi lớp 7B có bao nhiêu học sinh

$A . 35 h ọ c \sin h$

$B . 45 h ọ c \sin h$

$C . 40 h ọ c \sin h$

$D . 42 h ọ c \sin h$

Xem đáp án

Gọi $a, b, c$ lần lượt là số học sinh lớp $7 A, 7 B, 7 C$ .Theo tính chất dãy tỉ số bằng nhau ta có:

$\frac{a}{9} = \frac{b}{8} = \frac{c}{7} = \frac{a - c}{9 - 7} = \frac{10}{2} = 5 \Rightarrow b = 8.5 = 40$ .

Chọn đáp án C

Câu 21:

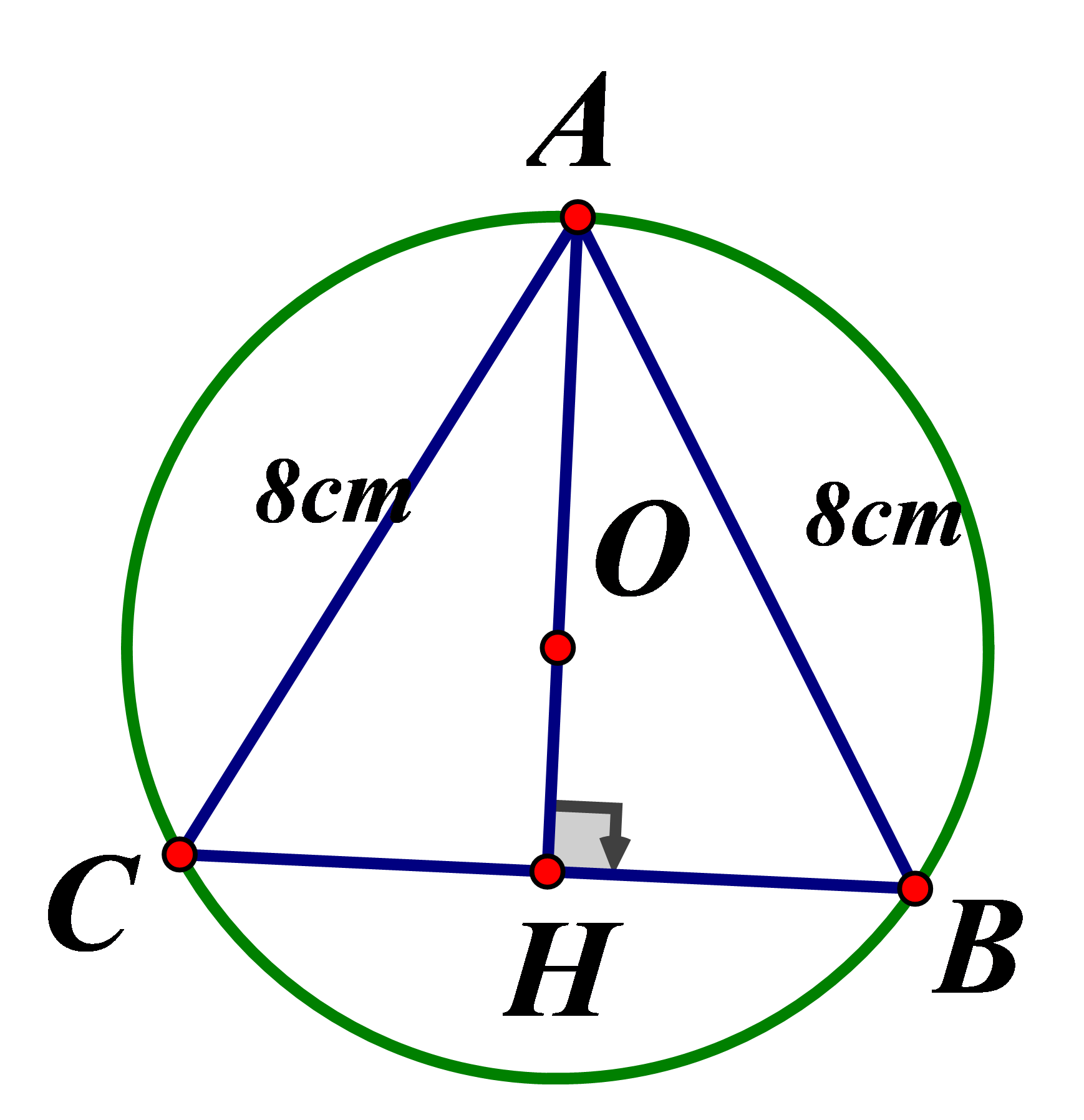
Cho $Δ A B C$ đều cạnh a nội tiếp $(O; R)$ và ngoại tiếp đường tròn $(I; r)$ . Khẳng định nào sau đây đúng ?

$A . I \equiv O, \frac{R}{r} = \frac{3}{2}$

$B . I \equiv O, \frac{R}{r} = 2$

$C . I \neq O, \frac{R}{r} = 2$

$D . I \neq O$

Xem đáp án

Hạ $A H$ là đường cao đồng thời là đường trung tuyến ,

Ta có $\frac{r}{R} = \frac{O H}{O A} = \frac{\frac{1}{3} A H}{\frac{2}{3} A H} = \frac{1}{2}$ . Chọn đáp án B

Câu 22:

Tính tổng P tất cả các giá trị của x thỏa mãn $\sqrt{{(- 2 x + 1)}^{2}} = 3$

$A . P = - 3$

$B . P = 3$

$C . P = 1$

$D . P = - 1$

Xem đáp án

$\sqrt{{(- 2 x + 1)}^{2}} = 3 \Leftrightarrow |- 2 x + 1| = 3 \Leftrightarrow [\begin{array}{l} - 2 x + 1 = 3 \\ - 1 + 2 x = 3 \end{array} \Leftrightarrow [\begin{array}{l} x = - 1 \\ x = 2 \end{array}$

Tổng các nghiệm $P = - 1 + 2 = 1$ . Chọn đáp án C

Câu 23:

Số dư của phép chia số $2018^{2018}$ cho số bằng $100$ bao nhiêu ?

$A .76$

$B .32$

$C .24$

$D .68$

Xem đáp án

$\begin{array}{l} 2018 \equiv 18 (\mod 100) \Rightarrow 2018^{2} \equiv 24 (\mod 100) \\ \Rightarrow 2018^{2018} \equiv 24^{1009} (\mod 100) = 24. {(24^{16})}^{63} = 24. {[{(24^{4})}^{4}]}^{63} \equiv 24. {[76^{4}]}^{63} (\mod 100) \\ \equiv 24.76 (\mod 100) \Rightarrow 2018^{2018} \equiv 24 (\mod 100) \end{array}$

Chọn đáp án C

Câu 24:

Hai tiếp tuyến $A, B$ tại của một đường tròn $(O)$ cắt nhau tại M và tạo thành $∠ A M B = 50^{0} .$ Tính số đo $∠ A O B$

$A . ∠ A O B = 110^{0}$

$B . ∠ A O B = 140^{0}$

$C . ∠ A O B = 120^{0}$

$D . ∠ A O B = 130^{0}$

Xem đáp án

Tứ giác có $A O B M$ :

$∠ A + ∠ O + ∠ B + ∠ M = 360 ° h a y 90 ° + ∠ O + 90 ° + 50 ° \Leftrightarrow ∠ O = 130 °$

Chọn đáp án D

Câu 25:

Tìm y biết $\frac{x - 2}{3} = \frac{y + 3}{2}$ và $x - y = 10$

$A . y = 7$

$B . y = 37$

$C . y = 27$

$D . y = 17$

Xem đáp án

Áp dụng dãy tỉ số bằng nhau

$\frac{x - 2}{3} = \frac{y + 3}{2} = \frac{x - 2 - y - 3}{3 - 2} = \frac{10 - 2 - 3}{1} = 5 \Rightarrow y + 3 = 10 \Rightarrow y = 7$

Chọn đáp án A

Câu 26:

Một tấm nhựa mỏng hình chữ nhật có diện tích $375 c m^{2}$ và chu vi là $80 c m$ . Tính chiều dài a và chiều rộng b của tấm nhựa đó .

$A . a = 75 c m, b = 5 c m$

$B . a = 125 c m, b = 3 c m$

$C . a = 25 c m, b = 15 c m$

$D . a = 60 c m, b = 20 c m$

Xem đáp án

Ta có $a + b = \frac{80}{2} = 40 (a, b > 0) \Rightarrow a = 40 - b$

$S = 375 \Leftrightarrow (40 - b) . b = 375 \Leftrightarrow b^{2} - 40 b + 375 = 0 \Leftrightarrow [\begin{array}{l} a = 25 \Rightarrow b = 15 (t m) \\ a = 15 \Rightarrow b = 25 (k t m) \end{array}$

Chọn đáp án C

Câu 27:

Tìm số tự nhiên n lớn nhất để $3 n + 19$ chia hết cho $n + 2$

$A . n = 13$

$B . n = 17$

$C . n = 11$

$D . n = 15$

Xem đáp án

$\begin{array}{l} \frac{3 n + 19}{n + 2} = \frac{3 (n + 2) + 13}{n + 2} = 3 + \frac{13}{n + 2} \\ \frac{3 n + 19}{n + 2} \in ℤ \Rightarrow 13 ⋮ (n + 2) \Rightarrow n + 2 = 13 \Leftrightarrow n = 11 \end{array}$

Chọn đáp án C

Câu 28:

Trong các hằng đẳng thức sau, hẳng đẳng thức nào đúng ?

$A . {(2 x - 3)}^{2} = 8 x^{3} - 36 x^{2} + 54 x - 27$

$B . {(2 x - 3)}^{2} = 8 x^{3} - 36 x^{2} + 54 x - 9$

$C . {(2 x - 3)}^{2} = 8 x^{3} - 36 x^{2} + 27 x - 27$

$D . {(2 x - 3)}^{2} = 8 x^{3} - 12 x^{2} + 54 x - 27$

Xem đáp án

Hẳng đẳng thức đúng là ${(2 x - 3)}^{2} = 8 x^{3} - 36 x^{2} + 54 x - 27$

Chọn đáp án A

Câu 29:

Cho $Δ A B C$ cân tại A. Biết $∠ A C B = 30^{0}, A B = 8 c m .$ Tính độ dài đường tròn ngoại tiếp $Δ A B C$

$A . C = 14 π c m$

$B . C = \frac{16}{3} π c m$

$C . C = 16 π c m$

$D . C = \frac{14}{5} π c m$

Xem đáp án

$A C = A B = 8 c m \Rightarrow A H = A C . \sin ∠ A C B = 8. \sin 30 ° = 4 (c m)$

$\Rightarrow R = A O = \frac{2}{3} A H = \frac{2}{3} .4 = \frac{8}{3} (c m) \Rightarrow P_{(O)} = 2 π R = 2 π . \frac{8}{3} = \frac{16 π}{3} (c m)$

Chọn đáp án B

Câu 30:

Gọi $x_{0}$ là nghiệm bé nhất của phương trình : $|3 x - 4| = |4 x - 3|$ . Tìm $x_{0}$

$A . x_{0} = 1$

$B . x_{0} = - 2$

$C . x_{0} = - 1$

$D . x_{0} = 2$

Xem đáp án

$|3 x - 4| = |4 x - 3| \Leftrightarrow [\begin{array}{l} 3 x - 4 = 4 x - 3 \\ 3 x - 4 = 3 - 4 x \end{array} \Leftrightarrow [\begin{array}{l} x = - 1 \\ x = 1 \end{array}$

Chọn đáp án C

Câu 31:

Tìm tất cả các giá trị của $a, b$ để hệ phương trình $\{\begin{cases} a x + y = - 5 \\ b x - a y = 1 \end{cases}$ có nghiệm $(x; y) = (2; 1)$

$A . a = - 3, b = 3$

$B . a = 3, b = 1$

$C . a = - 3, b = - 1$

$D . a = 3, b = - 1$

Xem đáp án

$\{\begin{cases} a x + y = - 5 \\ b x - a y = 1 \end{cases}$ có nghiệm $(x; y) = (2; 1)$ . Ta có:

$\{\begin{cases} 2 a + 1 = - 5 \\ - a + 2 b = 1 \end{cases} \Leftrightarrow \{\begin{cases} a = - 3 \\ b = - 1 \end{cases}$

Chọn đáp án D

Câu 32:

Tìm điều kiện của x để biểu thức $\sqrt{x^{2} + 2 x - 3}$ có nghĩa

$A . x \geq - 3$

$B . x \leq - 3 h o a c x \geq 1$

$C . x \leq 1$

$D . - 3 \leq x \leq 1$

Xem đáp án

để biểu thức $\sqrt{x^{2} + 2 x - 3}$ có nghĩa $x^{2} + 2 x - 3 \geq 0 [\begin{array}{l} x \leq - 3 \\ x \geq 1 \end{array}$

Chọn đáp án B

Câu 33:

Cho tứ giác ABCD nội tiếp đường tròn (O) .Gọi K là giao điểm của AB,CD .Biết $s d \overset{⏜}{A D} = 150^{0}, s d \overset{⏜}{B C} = 70^{0} .$ Tính số đo $∠ A K D$

$A . ∠ A K D = 80^{0}$

$B . ∠ A K D = 40^{0}$

$C . ∠ A K D = 50^{0}$

$D . ∠ A K D = 60^{0}$

Xem đáp án

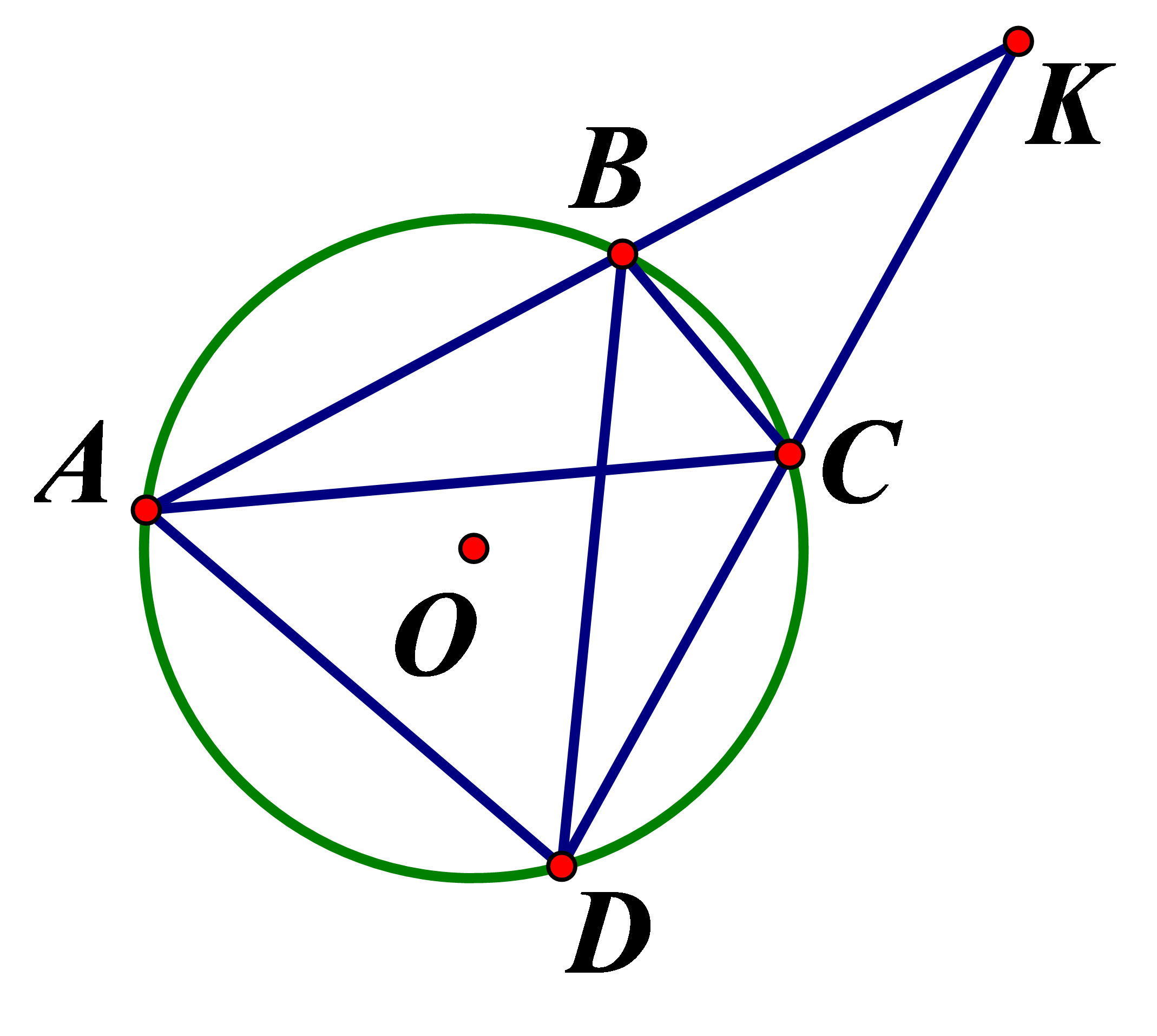
Áp dụng tính chất góc ở ngoài đường tròn , ta có :

$\Rightarrow ∠ A K D = \frac{1}{2} (s d \overset{⏜}{A D} - s d \overset{⏜}{B C}) = \frac{1}{2} (150 ° - 70 °) = 40 °$

Chọn đáp án B

Câu 34:

Cho $Δ A B C$ vuông tại A đường cao $A H .$ Biết $A C = 4 c m, B C = 5 c m .$ Tính độ dài đường cao AH

$A . A H = 2, 1 c m$

$B . A H = 2, 4 c m$

$C . A H = 2, 3 c m$

$D . A H = 2, 2 c m$

Xem đáp án

Áp dụng định lý Pytago $\Rightarrow A B = \sqrt{B C^{2} - A C^{2}} = \sqrt{5^{2} - 4^{2}} = 3 (c m)$

Áp dụng hệ thức lượng trong tam giác vuông

$\Rightarrow \frac{1}{A H^{2}} = \frac{1}{A B^{2}} + \frac{1}{A C^{2}} = \frac{1}{3^{2}} + \frac{1}{4^{2}} \Rightarrow A H = 2, 4 c m$

Chọn đáp án B

Câu 35:

Cho $Δ A B C$ vuông tại A. Biết $∠ B = 60^{0}, A B = 5 c m .$ Tính độ dài đoạn thẳng AC

$A . A C = 10 c m$

$B . A C = \frac{5 \sqrt{3}}{3} c m$

$C . A H = 2, 3 c m$

$D . A H = 2, 2 c m$

Xem đáp án

$A C = 5. \cot 60 ° = \frac{5 \sqrt{3}}{3} (c m)$

Chọn đáp án B

Câu 36:

Xác định hàm số $y = a x + b,$ biết đồ thị của hàm số đi qua điểm $M (- 1; 2)$ và song song với đường thẳng $y = 2 x - 3$

$A . y = 2 x - 4$

$B . y = x - 2$

$C . y = 2 x + 4$

$D . y = - x + 2$

Xem đáp án

$y = a x + b / / y = 2 x - 3 \Rightarrow \{\begin{cases} a = 2 \\ b \neq - 3 \end{cases}$

$y = 2 x + b q u a M (- 1; 2) \Rightarrow 2 = 2. (- 1) + b \Rightarrow b = 4$ $\Rightarrow y = 2 x + 4$

Chọn đáp án C

Câu 37:

Phương trình $a x^{2} + b x + c = 0 (a \neq 0)$ có biệt thức $Δ' = b'^{2} - a c > 0$ $(b' = \frac{b}{2})$ . Kết luận nào sau đây đúng ?

$A . P h ư ơ n g t r ì n h c ó h a i n g h i ệ m x_{1} = x_{2} = - \frac{b}{2 a}$

$B . P h ư ơ n g t r ì n h c ó h a i n g h i ệ m p h â n b i ệ t x_{1} = \frac{- b' + \sqrt{Δ'}}{2 a}, x_{2} = \frac{- b' - \sqrt{Δ'}}{2 a}$

$C . P h ư ơ n g t r ì n h v ô n g h i ệ m$

$D . P h ư ơ n g t r ì n h c ó h a i n g h i ệ m p h â n b i ệ t x_{1} = \frac{- b' + \sqrt{Δ'}}{a}, x_{2} = \frac{- b' - \sqrt{Δ'}}{a}$

Xem đáp án

Vì $Δ' > 0$ nên Phương trình có hai nghiệm phân biệt

$x_{1} = \frac{- b' + \sqrt{Δ'}}{a}, x_{2} = \frac{- b' - \sqrt{Δ'}}{a}$

Chọn đáp án D

Câu 38:

Cho đường tròn $(O; 5 c m)$ , dây $M N = 8 c m .$ Đoạn thẳng $O I ⊥ M N (I \in M N)$ .Tính độ dài đoạn thẳng OI

$A . O I = 3, 5 c m$

$B . O I = 4 c m$

$C . O I = 5 c m$

$D . O I = 3 c m$

Xem đáp án

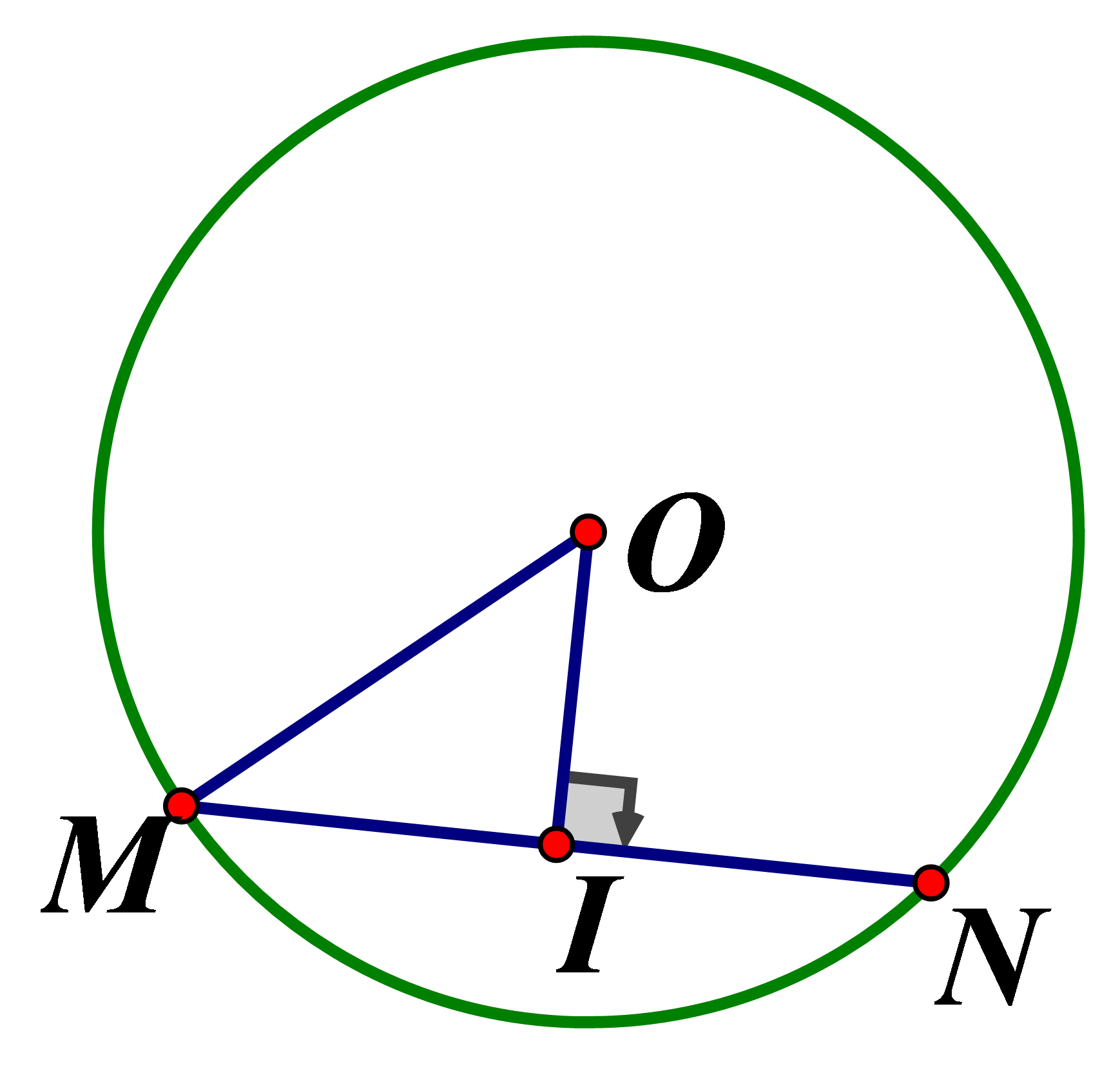
Vì $O I ⊥ M N \Rightarrow I$ là trung điểm MN $\Rightarrow M I = 4 c m$

$\Rightarrow O I = \sqrt{O M^{2} - M I^{2}} = \sqrt{5^{2} - 4^{2}} = 3 c m$

Chọn đáp án D

Câu 39:

Cho phương trình $x^{2} - 2 (m - 3) x + 2 m - 7 = 0 (1)$ . Gọi hai nghiệm của phương trình $(1)$ là $x_{1}, x_{2},$ tìm tất cả các giá trị của m để $\frac{1}{x_{1} + 1} + \frac{1}{x_{2} + 1} = m$

$A . m = \frac{2 - \sqrt{33}}{4}$

$B . m = \frac{7 + \sqrt{33}}{4}$

$C . m = \frac{2 \pm \sqrt{33}}{4}$

$D . m = \frac{7 \pm \sqrt{33}}{4}$

Xem đáp án

$\begin{array}{l} x^{2} - 2 (m - 3) x + 2 m - 7 = 0 (1) \\ Δ' = {(m - 3)}^{2} - (2 m - 7) = {(m - 4)}^{2} \geq 0 (\forall m) \end{array}$

Nên phương trình (1) luôn có nghiệm

Theo Vi-et ta có: $\{\begin{cases} x_{1} + x_{2} = 2 (m - 3) \\ x_{1} x_{2} = 2 m - 7 \end{cases}$ . Theo bài ta có :

$\begin{array}{l} \frac{1}{x_{1} + 1} + \frac{1}{x_{2} + 1} = m \Leftrightarrow \frac{x_{1} + x_{2} + 2}{(x_{1} + 1) (x_{2} + 1)} = m \Leftrightarrow \frac{x_{1} + x_{2} + m}{x_{1} + x_{2} + x_{1} x_{2} + 1} = m \\ \Leftrightarrow \frac{2 (m - 3) + 2}{2 (m - 3) + 2 m - 7 + 1} = m \Leftrightarrow \frac{2 m - 4}{4 m - 12} = m \Leftrightarrow \frac{m - 2}{2 m - 6} = m \\ \Rightarrow m - 2 = 2 m^{2} - 6 m \Leftrightarrow 2 m^{2} - 7 m + 2 = 0 \Leftrightarrow m = \frac{7 \pm \sqrt{33}}{4} \end{array}$

Chọn đáp án D

Câu 40:

Tứ giác $A B C D$ nội tiếp có $∠ A B C = 80^{0}$ và $∠ B C D = 100^{0} .$ Tính hiệu của $∠ A D C - ∠ B A C$

$A . ∠ A D C - ∠ B A C = 20^{0}$

$B . ∠ A D C - ∠ B A C = 10^{0}$

$C . ∠ A D C - ∠ B A C = 45^{0}$

$D . ∠ A D C - ∠ B A C = 25^{0}$

Xem đáp án

$\begin{array}{l} ∠ A B C = 80^{0} \Rightarrow ∠ A D C = 180 ° - 80 ° = 100 ° \\ ∠ B C D = 100^{0} \Rightarrow ∠ B A D = 180 ° - 100 ° = 80 ° \end{array}$ $∠ A D C - ∠ B A C = 20^{0}$

Chọn đáp án A

Câu 41:

Tính tổng T các số tự nhiên chia hết cho cả 2 và 3 nhưng nhỏ hơn 100.

$A . T = 816$

$B . T = 1632$

$C . T = 765$

$D .867$

Xem đáp án

Các số cần tìm là $0; 6; 12; ....; 84; 90; 96$

Bài toán đưa về tìm tổng của dãy số trên.

Số số hạng : $(96 - 0) : 6 + 1 = 17$ (số)

$T = 96.17 : 2 = 816$

Chọn đáp án A

Câu 42:

Độ dài cung có số đo $α °$ , của đường tròn $(O; R)$ được tính theo công thức nào dưới đây ?

$A . \frac{π R α}{180}$

$B . \frac{π R^{2} α}{180}$

$C . \frac{π R α^{2}}{180}$

$D . \frac{π R n}{180}$

Xem đáp án

$l = \frac{π R α}{180}$

Chọn đáp án A

Câu 43:

Cho hình vuông $A B C D$ có tâm O, cạnh $4 c m .$ Vẽ hai đường tròn $(O_{1}; 1 c m)$ và $(O_{2}; 1 c m)$ tiếp xúc với hai cạnh $A B, C D$ của hình vuông và tiếp xúc nhau tại O. Vẽ hai đường tròn $(O_{3})$ và $(O_{4})$ tiếp xúc với hai cạnh AD, BC của hình vuông và mỗi đường tròn đều tiếp xúc với cả hai đường tròn $(O_{1})$ và $(O_{2})$ . Tính tổng diện tích S của các hình tròn $(O_{1}), (O_{2}), (O_{3}), (O_{4})$

$A . S = \frac{26}{3} π (c m^{2})$

$B . S = \frac{25}{3} (c m^{2})$

$C . S = \frac{26}{9} π (c m^{2})$

$D . S = \frac{24}{9} π (c m^{2})$

Xem đáp án

Chọn đáp án C

Câu 44:

Cho $Δ A B C$ vuông tại A, đường cao AH Khẳng định nào sau đây đúng ?

$A . \frac{1}{A H^{2}} = \frac{1}{A B^{2}} + \frac{1}{B C^{2}}$

$B . \frac{1}{A H^{2}} = \frac{1}{A B^{2}} + \frac{1}{A C^{2}}$

$C .. \frac{1}{A H^{2}} = \frac{1}{B C^{2}} + \frac{1}{A C^{2}}$

$D .. \frac{1}{A H^{2}} = \frac{1}{H B^{2}} + \frac{1}{H C^{2}}$

Xem đáp án

Áp dụng hệ thức lượng trong tam giác vuông $\frac{1}{A H^{2}} = \frac{1}{A B^{2}} + \frac{1}{A C^{2}}$ , đúng

Chọn đáp án B

Câu 45:

Cho $Δ A B C$ có $∠ A = 80^{0}$ nội tiếp đường tròn $(O; R)$ . Tính diện tích S của hình quạt tròn $O B C$ (chứa cung nhỏ $B C)$

$A . S = \frac{4 π R^{2}}{9}$

$B . \frac{2 π R^{2}}{3}$

$C . \frac{4 π R^{2}}{3}$

$D . \frac{2 π R^{2}}{9}$

Xem đáp án

$∠ A = 80^{0} \Rightarrow s d \overset{⏜}{B C} = 160 °$

$S_{q u a t} = \frac{π R^{2} n}{360 °} = \frac{π R .160}{360} = \frac{4 π R}{9} (c m^{2})$

Chọn đáp án A

Câu 46:

Cho $Δ A B C$ vuông tại A, đường cao AH .Biết $\frac{B H}{H C} = \frac{9}{16}, A H = 48 c m .$ Tính độ dài cạnh AB:

$A . A B = 65 c m$

$B . A B = 55 c m$

$C . A B = 50 c m$

$D . A B = 60 c m$

Xem đáp án

Vì $\frac{B H}{H C} = \frac{9}{16}, A H = 48 c m \Rightarrow 9 k .16 k = 48^{2} \Rightarrow k = 4 \Rightarrow B H = 36$

$A B = \sqrt{A H^{2} + B H^{2}} = \sqrt{48^{2} + 36^{2}} = 60 c m$

Chọn đáp án D

Câu 47:

Rút gọn biểu thức $A = \sqrt{{(2 - \sqrt{5})}^{2}}$ . Kết quả nào sau đây đúng ?

$A . A = \sqrt{5} - 2$

$B . A = \sqrt{2} - \sqrt{5}$

$C . A = 2 - \sqrt{5}$

$D . A = \sqrt{5} - \sqrt{2}$

Xem đáp án

$A = \sqrt{{(2 - \sqrt{5})}^{2}} = |2 - \sqrt{5}| = \sqrt{5} - 2$

Chọn đáp án A

Câu 48:

Tính diện tích xung quanh của hình lăng trụ đứng $A B C . A' B' C'$ có kích thước như hình vẽ bên

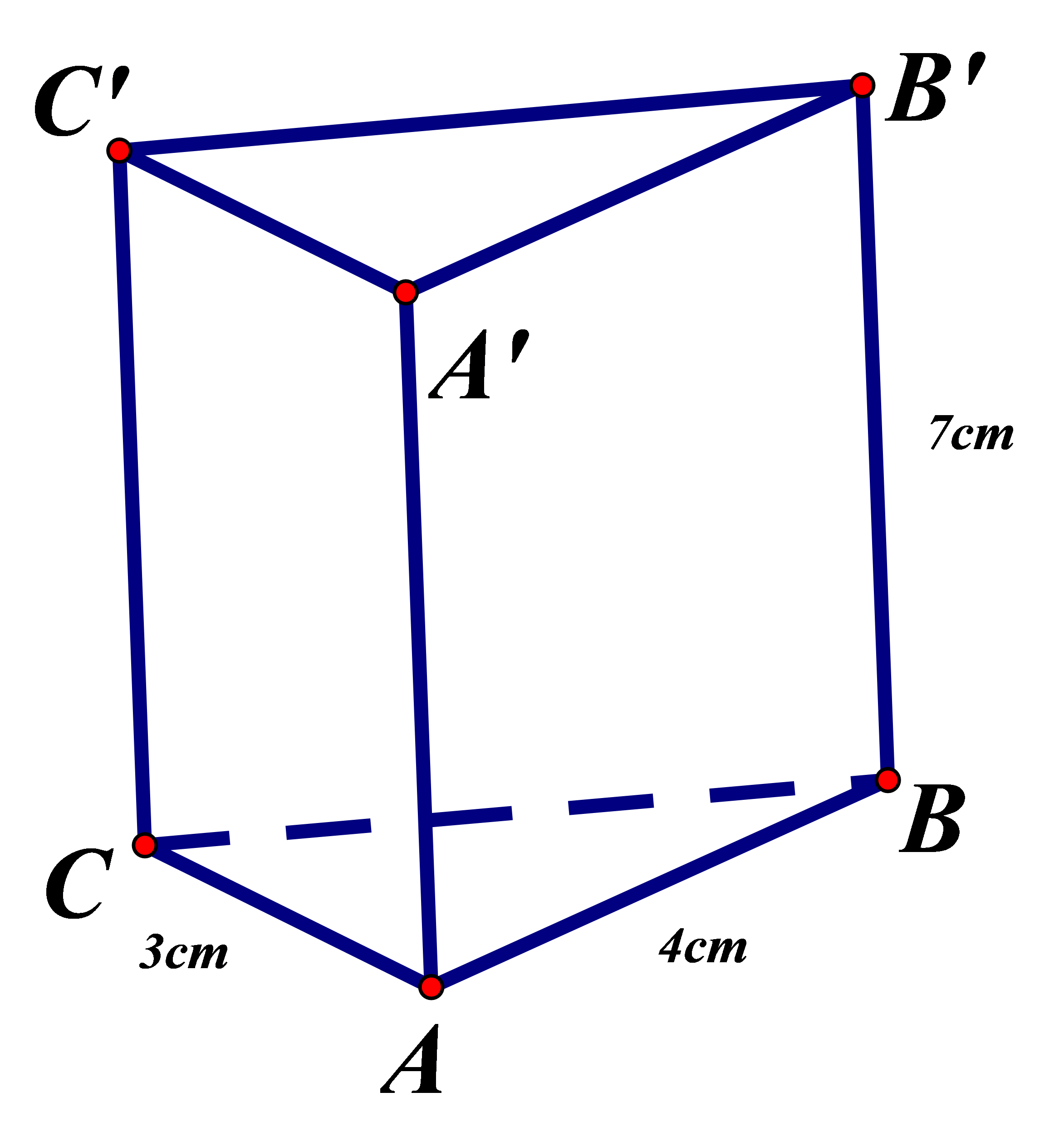
Media VietJack

$A .42 c m^{2}$

$B .84 c m^{2}$

$C .48 c m^{2}$

$D .96 c m^{2}$

Xem đáp án

Áp dụng định lý Pytago $\Rightarrow B C = \sqrt{3^{2} + 4^{2}} = 5 (c m)$

$\Rightarrow S_{x q} = P h = (3 + 4 + 5) .7 = 84 c m^{2}$

Chọn đáp án B

Câu 49:

Rút gọn biểu thức $A = \frac{y^{2}}{3 a b} . \sqrt{\frac{9 a^{3} b^{4}}{x y^{3}}}$ với $a, b, x, y$ là các số dương. Kết quả nào sau đây đúng ?

$A . A = a y \sqrt{\frac{b}{x y}}$

$B . A = b y \sqrt{\frac{a}{x}}$

$C . A = b y \sqrt{\frac{a}{x y}}$

$D . A = y \sqrt{\frac{a b}{x y}}$

Xem đáp án

$A = \frac{y^{2}}{3 a b} . \sqrt{\frac{9 a^{3} b^{4}}{x y^{3}}} = \frac{y^{2}}{3 a b} . \frac{\sqrt{9 a^{3} b^{4}}}{\sqrt{x y^{3}}} = \frac{y^{3}}{3 a b} . \frac{3. a . b^{2} \sqrt{a}}{y \sqrt{x y}} = \frac{y b \sqrt{a y}}{\sqrt{x}}$

Chọn đáp án C

Câu 50:

Cho $Δ A B C$ vuông tại A biết $A B = 6 c m, B C = 10 c m .$ Đường phân giác ngoài của góc ngoài tại đỉnh B cắt tia CA tại E. Tính độ dài đoạn thẳng BE

$A . B E = 2 \sqrt{5} c m$

$B . B E = 6 \sqrt{5} c m$

$C . B E = 4 \sqrt{5} c m$

$D . B E = 5 \sqrt{5} c m$

Xem đáp án

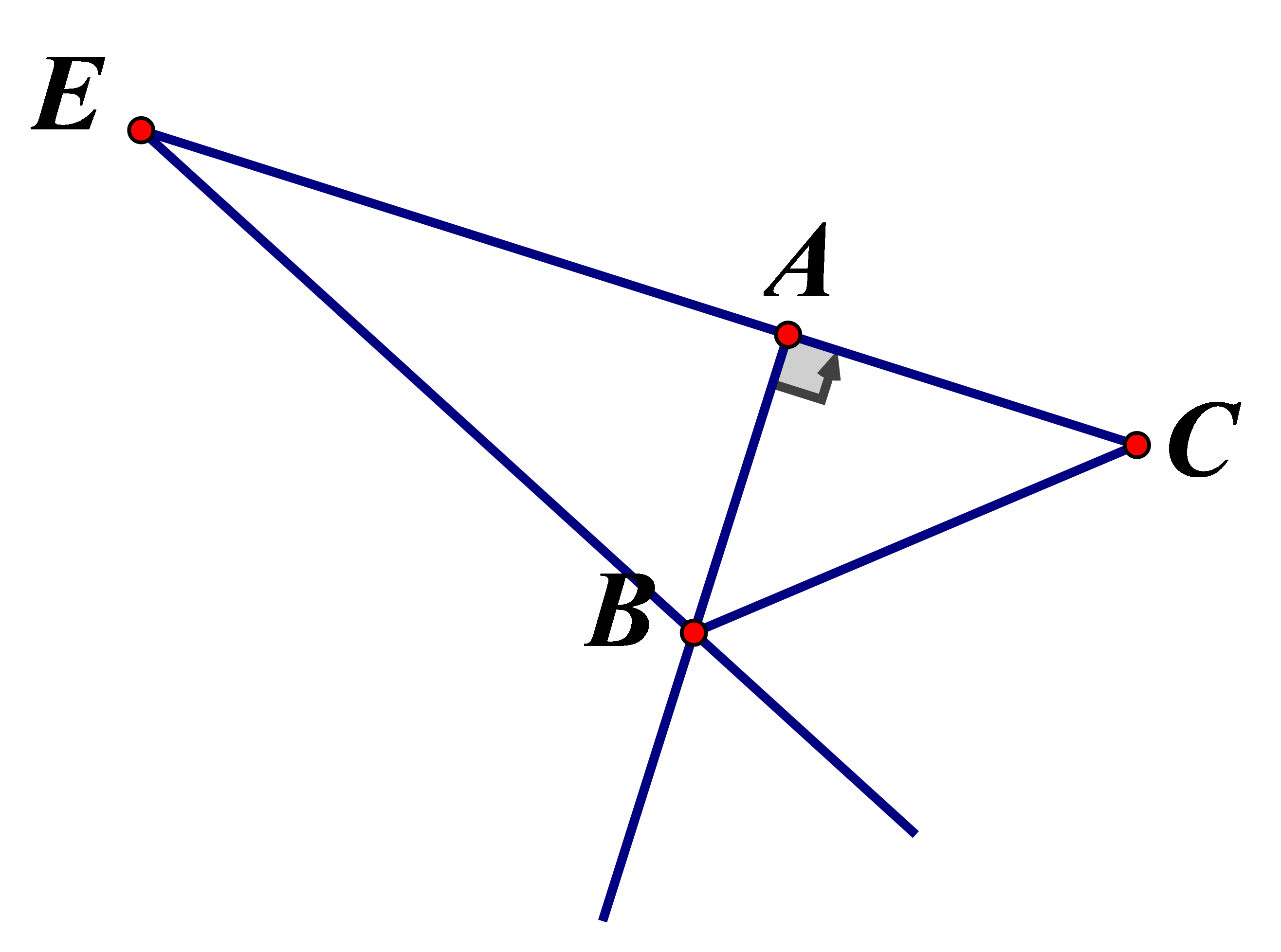
$Δ A B C$ vuông tại A $\Rightarrow A C = \sqrt{B C^{2} - A B^{2}} = \sqrt{10^{2} - 6^{2}} = 4 (c m)$

Vì BE là phân giác ngoài tại đỉnh B

$\Rightarrow \frac{E C}{E A} = \frac{B C}{B A} = \frac{E C}{E C + A C} = \frac{B C}{B A} \Rightarrow E C . B A = B C . (E C + A C)$

$\Leftrightarrow E C . (B C - B A) = B C . A C \Leftrightarrow E C = \frac{B C . A C}{B A - B C} = \frac{10.4}{10 - 6} = 10 c m$

$\Rightarrow B E = 6 \sqrt{5}$

Chọn đáp án B