50 câu hỏi trắc nghiệm thuộc Bộ 30 đề thi vào 10 môn Toán có lời giải chi tiết (Đề 22)

Câu 1:

Cho tam giác ABC vuông tại A. Hệ thức nào sau đây sai ?

$A . \sin^{2} B + \sin^{2} C = 1$

$B . \cos B = \cos C$

$C . \sin B = \cos C$

$D . \tan B = \cot C$

Xem đáp án

Hệ thức sai là

\cos B = \cos C

.Chọn đáp án B

Câu 2:

Đồ thị ở hình bên dưới là đồ thị của hàm số nào trong các hàm số sau :

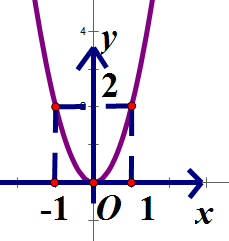
Media VietJack

$A . y = 4 x^{2}$

$B . y = 2 x^{2}$

$C . y = \frac{1}{4} x^{2}$

$D . y = \frac{1}{2} x^{2}$

Xem đáp án

Đồ thị hàm số $y = a x^{2}$ đi qua $(1; 2) \Rightarrow 2 = a {.1}^{2} \Rightarrow a = 2$

Chọn đáp án B

Câu 3:

Cho tứ giác ABCD có $∠ A = ∠ B, ∠ C = ∠ D .$ Khẳng định nào sau đây là đúng ?

$A . T ứ g i á c A B C D l à h ì n h c h ữ n h ậ t$

$B . T ứ g i á c A B C D l à h ì n h v u ô n g$

$C . T ứ g i á c A B C D l à h ì n h t h a n g c â n$

$D . T ứ g i á c A B C D l à h ì n h t h o i .$

Xem đáp án

Tứ giác có 2 cặp cạnh kề bằng nhau là hình thang cân

Chọn đáp án C

Câu 4:

Cho tam giác đều ABC có diện tích bằng $4 \sqrt{3} (c m^{2})$ .Tam giác MNP đồng dạng với tam giác ABC theo tỉ số đồng dạng $k = \frac{1}{2} .$ Tính độ dài MN

$A . M N = 2 (c m)$

$B . M N = 6 (c m)$

$C . M N = 8 (c m)$

$D . M N = 4 (c m)$

Xem đáp án

Vì $Δ M N P ∽ Δ A B C$ theo $k = \frac{1}{2} \Rightarrow \frac{S_{M N P}}{S_{A B C}} = \frac{1}{4} \Rightarrow S_{M N P} = \sqrt{3}$

Mà $S_{M N P} = \frac{M N^{2} \sqrt{3}}{4} \Rightarrow \frac{M N^{2} \sqrt{3}}{4} = \sqrt{3} \Leftrightarrow M N^{2} = 4 \Leftrightarrow M N = 2 (c m)$

Chọn đáp án A

Câu 5:

Tìm nghiệm của phương trình $3 x - 5 = 9 - 4 x$

$A . x = 2$

$B . x = \frac{4}{7}$

$C . x = - 4$

$D . x = - 2$

Xem đáp án

$3 x - 5 = 9 - 4 x \Leftrightarrow 7 x = 14 \Leftrightarrow x = 2$

Chọn đáp án A

Câu 6:

Chia đa thức $6 x^{3} - 7 x^{2} - x + 2$ cho đa thức $2 x + 1$ ta được két quả nào sau đây ?

$A .3 x^{2} - 5 x + 2$

$B .3 x^{2} + 5 x - 2$

$C .3 x^{2} - 5 x - 2$

$D .3 x^{2} + 5 x + 2$

Xem đáp án

Thực hiện phép chia $6 x^{3} - 7 x^{2} - x + 2$ cho đa thức $2 x + 1$

Ta được thương là $3 x^{2} - 5 x + 2$ .Chọn đáp án A

Câu 7:

Giải hệ phương trình $\{\begin{cases} 2 x + 3 y = 1 \\ 3 x + y = - 2 \end{cases}$

$A . (x; y) = (- 1; - 1)$

$B . (x; y) = (1; 1)$

$C . (x; y) = (1; - 1)$

$D . (x; y) = (- 1; 1)$

Xem đáp án

$\{\begin{cases} 2 x + 3 y = 1 \\ 3 x + y = - 2 \end{cases} \Leftrightarrow \{\begin{cases} 2 x + 3 y = 1 \\ - 9 x - 3 y = 6 \end{cases} \Leftrightarrow \{\begin{cases} - 7 x = 7 \\ y = - 2 - 3 x \end{cases} \Leftrightarrow \{\begin{cases} x = - 1 \\ y = 1 \end{cases}$

Chọn đáp án D

Câu 8:

Thực hiện phép tính $5 x (3 x^{2} + 2)$

$A .15 x^{2} + 10$

$B .15 x^{2} + 10 x$

$C .5 x^{2} + 10 x$

$D .15 x^{2} + 5 x$

Xem đáp án

$5 x (3 x^{2} + 2) = 15 x^{3} + 10 x$

Chọn đáp án B

Câu 9:

Cho các tập hợp $ M = \{0; 2; 4\}, N = \{1; 3\}, P = \{1; 2; 3; 4\}$ . Khẳng định nào sau đây đúng ?

$A . N \subset P$

$B . M \cap N = P$

$C . M \subset P$

$D . M \cup N = P$

Xem đáp án

$N \subset P$ .Chọn đáp án A

Câu 10:

Cho các tập hợp số $ℕ, ℤ, ℚ, ℝ$ . Khẳng định nào sau đây sai ?

$A . ℚ \subset ℝ$

$B . ℚ \cup ℝ = ℝ$

$C . ℕ \cap ℤ = ℚ$

$D . ℕ \subset ℚ$

Xem đáp án

Khẳng định sai là $ℕ \cap ℤ = ℚ$ Chọn đáp án C

Câu 11:

Đẳng thức nào sau đây đúng với mọi $x > 4$

$A . \sqrt{x^{2} + 9} = x + 3$

$B . \sqrt{4 - 4 x + x^{2}} = 2 - x$

$C . \sqrt{1 - 2 x + x^{2}} = 1 - x$

$D . \sqrt{x^{2} - 6 x + 9} = x - 3$

Xem đáp án

$x > 4 \Rightarrow x > 3 \Rightarrow \sqrt{x^{2} - 6 x + 9} = \sqrt{{(x - 3)}^{2}} = |x - 3| = x - 3 (d o x > 3)$

Chọn đáp án D

Câu 12:

Tính diện tích xung quanh

S_{x q}

của hình trụ có bán kính đáy

r = 10 c m

và chiều cao

h = 30 c m

$A . S_{x q} = 400 π (c m^{2})$

$B . S_{x q} = 500 π (c m^{2})$

$C . S_{x q} = 600 π (c m^{2})$

$D . S_{x q} = 300 π (c m^{2})$

Xem đáp án

$S_{x q} = 2 π r h = 2 π .10.30 = 600 π$

Chọn đáp án C

Câu 13:

Cho

Q = {(\sqrt{2 - \sqrt{3}} + \sqrt{2 + \sqrt{3}})}^{2} .

Khẳng định nào sau đây đúng ?

$A . Q = 6^{2}$

$B . Q = 3$

$C . Q = 6$

$D . Q = 3^{2}$

Xem đáp án

$Q = {(\sqrt{2 - \sqrt{3}} + \sqrt{2 + \sqrt{3}})}^{2} = 2 - \sqrt{3} + 2 + \sqrt{3} + 2 \sqrt{(2 - \sqrt{3}) (2 + \sqrt{3})} = 4 + 2.1 = 6$

Chọn đáp án C

Câu 14:

Tìm giá trị nhỏ nhất $y_{\min}$ của hàm số $y = \sqrt{3} x^{2}$

$A . y_{\min} = - \frac{1}{2}$

$B . y_{\min} = 2$

$C . y_{\min} = 0$

$D . y_{\min} = 1$

Xem đáp án

$x^{2} \geq 0 \Leftrightarrow y = \sqrt{3} x^{2} \geq 0 \Leftrightarrow y_{\min} = 0$

Chọn đáp án C

Câu 15:

Giải phương trình $2 x^{2} - 5 x + 2 = 0$

$A . x_{1} = - \frac{1}{2}, x_{2} = 2$

$B . x_{1} = \frac{1}{2}, x_{2} = 2$

$C . x_{1} = - \frac{1}{2}, x_{2} = - 2$

$D . x_{1} = \frac{1}{2}, x_{2} = - 2$

Xem đáp án

$2 x^{2} - 5 x + 2 = 0 \Leftrightarrow [\begin{array}{l} x = 2 \\ x = \frac{1}{2} \end{array}$

Chọn đáp án B

Câu 16:

Tại thời điểm tia sáng mặt trời tạo với mặt đất một góc 40⁰ người ta đo được bóng của một cột cờ là 15(m). Hỏi chiều cao của cột cờ là bao nhiêu (kết quả làm tròn đến chữ số thập phân thứ hai)

$A . h \approx 11, 59 m$

$B . h \approx 12, 69 m$

$C . h \approx 13, 59 m$

$D . h \approx 12, 59 m$

Xem đáp án

Áp dụng lượng giác trong tam giác vuông

$h = 15. \tan 40 ° \approx 12, 59 (m)$ .Chọn đáp án D

Câu 17:

Xác định hàm số $y = a x + b,$ biết đồ thị của hàm số song song với đường thẳng $y = - 3 x + 5$ và đi qua điểm $A (- 2; 2)$

$A . y = \frac{3}{2} x + 5$

$B . y = - 3 x - 4$

$C . y = - 3 x + 4$

$D . y = \frac{1}{2} x - 5$

Xem đáp án

Đồ thị hàm số $y = a x + b$ song song với đường thẳng $y = - 3 x + 5$

$\Rightarrow \{\begin{cases} a = - 3 \\ b \neq 5 \end{cases}$ . Đồ thị hàm số $y = - 3 x + b$ đi qua $A (- 2; 2)$

$\Rightarrow 2 = (- 3) . (- 2) + b \Rightarrow b = - 4$ (tm)

Vậy đường thẳng cần tìm là Chọn đáp án B

Câu 18:

Tính $M = \sqrt{25} - \sqrt{16}$

$A . M = 4$

$B . M = 3$

$C . M = 1$

$D . M = 2$

Xem đáp án

$M = \sqrt{25} - \sqrt{16} = 5 - 4 = 1$

Chọn đáp án C

Câu 19:

Một hình nón có diện tích mặt đáy bằng $4 π (c m^{2})$ và diện tích xung quanh bằng $8 π (c m^{2})$ . Tính chiều cao h của hình nón đó.

$A . h = 2 (c m)$

$B . h = 2 \sqrt{5} (c m)$

$C . h = 3 (c m)$

$D . h = 2 \sqrt{3} (c m)$

Xem đáp án

$S_{d a y} = π R^{2} = 4 π \Rightarrow R = 2, S_{x q} = π R l = 8 π \Leftrightarrow π .2 l = 8 π \Rightarrow l = 4$ $h = \sqrt{l^{2} - R^{2}} = \sqrt{4^{2} - 2^{2}} = 2 \sqrt{3} (c m)$

Chọn đáp án D

Câu 20:

Tìm điều kiện của m để hàm số $y = (2 m - 1) x + m + 2$ luôn nghịch biến

$A . m \leq \frac{1}{2}$

$B . m > \frac{1}{2}$

$C . m < \frac{1}{2}$

$D . m \geq \frac{1}{2}$

Xem đáp án

để hàm số $y = (2 m - 1) x + m + 2$ luôn nghịch biến thì $2 m - 1 > 0 \Leftrightarrow m > \frac{1}{2}$

Chọn đáp án B

Câu 21:

Tìm số tự nhiên n có hai chữ số, biết rằng hai lần chữ số hàng đơn vị lớn hơn chữ số hàng chục 1 đơn vi và nếu viết hai chữ số ấy theo thứ tự ngược lại thì được một số mới có hai chữ số bé hơn số cũ 27 đơn vị

$A . n = 52$

$B . n = 47$

$C . n = 25$

$D . n = 74$

Xem đáp án

Gọi $n = \bar{a b} (0 < a, b < 10, a, b \in ℕ)$ . Theo bài ta có hệ phương trình :

$\{\begin{cases} a - 2 b = - 1 \\ \bar{a b} - \bar{b a} = 27 \end{cases} \Leftrightarrow \{\begin{cases} a - 2 b = - 1 \\ 9 a - 9 b = 27 \end{cases} \Leftrightarrow \{\begin{cases} a = 7 \\ b = 4 \end{cases} (t m)$

Vậy số cần tìm là 74. Chọn đáp án D

Câu 22:

Tìm nghiệm của phương trình $\sqrt{\frac{2 x - 3}{x - 1}} = 2$

$A . x = - 2$

$B . x = 1$

$C . x = - \frac{1}{3}$

$D . x = \frac{1}{2}$

Xem đáp án

$\sqrt{\frac{2 x - 3}{x - 1}} = 2 (x \geq \frac{3}{2} \cup x \leq 1) \Rightarrow \frac{2 x - 3}{x - 1} = 4 \Rightarrow 2 x - 3 = 4 x - 4 \Leftrightarrow x = \frac{1}{2} (t m)$

Chọn đáp án D

Câu 23:

Cho hai số x,y thỏa mãn $\frac{x}{5} = \frac{y}{3}$ và $x - y = 4.$ Tính $T = x y$

$A . T = 50$

$B . T = 70$

$C . T = 40$

$D . T = 60$

Xem đáp án

$\frac{x}{5} = \frac{y}{3} = \frac{x - y}{5 - 3} = \frac{4}{2} = 2 \Rightarrow \{\begin{cases} x = 10 \\ y = 6 \end{cases} \Rightarrow x y = 60$

Chọn đáp án D

Câu 24:

Cho hai điểm A,B thuộc đường tròn (O) .Hai tiếp tuyến của (O) tại B,C cắt nhau tại A biết

∠ B A C = 40^{0} .

Tính

∠ B O C

$A . ∠ B O C = 70^{0}$

$B . ∠ B O C = 140^{0}$

$C . ∠ B O C = 90^{0}$

$D . ∠ B O C = 40 °$

Xem đáp án

tiếp tuyến của (O) tại B,C cắt nhau tại $A \Rightarrow ∠ A B O = ∠ A C O = 90 °$

Tứ giác AOBC có $∠ A + ∠ B + ∠ O + ∠ C = 360 °$

Hay $40 ° + 90 ° + ∠ O + 90 ° = 220 ° \Rightarrow ∠ O = 140 °$

Chọn đáp án B

Câu 25:

Điểm nào sau đây không thuộc đồ thị hàm số $y = 2 x^{2}$

$A . N (0; 0)$

$B . M (2; 4)$

$C . Q (1; 2)$

$D . P (- 1; 2)$

Xem đáp án

Ta thay lần lượt các điểm vào hàm só $y = 2 x^{2}$ có điêm $M (2; 4)$ không thỏa

Chọn đáp án B

Câu 26:

Phương trình bậc hai $a x^{2} + b x + c = 0 (a \neq 0)$ có biệt thức $Δ = b^{2} - 4 a c = 0.$ Khẳng định nào sau đây đúng ?

$A . P h ư ơ n g t r ì n h c ó v ô s ố n g h i ệ m$

$B . P h ư ơ n g t r ì n h c ó n g h i ệ m k é p$

$C . P h ư ơ n g t r ì n h c ó h a i n g h i ệ m p h â n b i ệ t$

$D . P h ư ơ n g t r ì n h v ô n g h i ệ m$

Xem đáp án

Vì $Δ = 0$ nên phương trình có nghiệm kép

Chọn dáp án B

Câu 27:

Tính góc nhọn $α$ tạo bởi đường thẳng $y = \sqrt{3} x + \frac{1}{2}$ với trục $O x$

$A . α = 75^{0}$

$B . α = 60^{0}$

$C . α = 45^{0}$

$D . α = 30^{0}$

Xem đáp án

Vì $a$ (hệ số góc) là $\sqrt{3}$ nên $\tan α = \sqrt{3} \Rightarrow α = 60 °$

Chọn đáp án B

Câu 28:

Cho tam giác cân ABC biết $A B = 4 (c m)$ và chu vi của tam giác bằng $22 (c m) .$ Tính độ dài cạnh BC

$A . B C = 9 (c m)$

$B . B C = 8 (c m)$

$C . B C = 14 (c m)$

$D . B C = 4 (c m)$

Xem đáp án

Nếu $A B = 4 c m$ là cạnh bên thì $B C = 22 - 2.4 = 14 (c m)$ khi đó $B C > A B + A C (14 > 4 + 4)$ . Trái với bất đẳng thức tam giác nên $A B = 4 c m$ là cạnh đáy $\Rightarrow B C = \frac{22 - 4}{2} = 9 c m$ .Chọn đáp án A

Câu 29:

Cho biểu thức $M = \sqrt{{(3 - \sqrt{15})}^{2}}$ .Khẳng định nào sau đây đúng ?

$A . M = \sqrt{15} - \sqrt{3}$

$B . M = \sqrt{3} - \sqrt{15}$

$C . M = \sqrt{15} - 3$

$D . M = 3 - \sqrt{15}$

Xem đáp án

$M = \sqrt{{(3 - \sqrt{15})}^{2}} = |3 - \sqrt{15}| = \sqrt{15} - 3 (d o \sqrt{15} > 3)$

Chọn đáp án C

Câu 30:

Cho tam giác ABC có

A B = 2 (c m), B C = 5 (c m), C A = 6 (c m) .

Bất đẳng thức nào sau đây đúng

$A . ∠ B > ∠ C > ∠ A$

$B . ∠ A > ∠ B > C$

$C . ∠ C > ∠ B > ∠ A$

$D . ∠ B > ∠ A > ∠ C$

Xem đáp án

$\begin{array}{l} A B = 2 (c m), B C = 5 (c m), C A = 6 (c m) \\ \Rightarrow A C > B C > A B \Rightarrow ∠ B > ∠ A > ∠ C \end{array}$

(quan hệ giữa cạnh và góc trong tam giác)

Chọn đáp án D

Câu 31:

Hệ phương trình nào sau đây có vô số nghiệm ?

$A . \{\begin{cases} - 2 x + y = - 3 \\ x + y = 1 \end{cases}$

$B . \{\begin{cases} 3 x + 2 y = 3 \\ 2 x + 3 y = 2 \end{cases}$

$C . \{\begin{cases} - x + y = 2 \\ 2 x + y = 3 \end{cases}$

$D . \{\begin{cases} 3 x - 2 y = 2 \\ - 3 x + 2 y = - 2 \end{cases}$

Xem đáp án

Hệ có vô số nghiệm khi $\frac{a}{a'} = \frac{b}{b'} = \frac{c}{c'}$ nên sai đề

Câu 32:

Tìm điều kiện của x để biểu thức $\sqrt{- x^{2} + 6 x - 9}$ xác định ?

$A . x = 3$

$B . x \in R$

$C . x \neq 3$

$D . K h ô n g c ó g i á t r ị x$

Xem đáp án

biểu thức $\sqrt{- x^{2} + 6 x - 9}$ xác định thì

$- x^{2} + 6 x - 9 \geq 0$ mà $- x^{2} + 6 x - 9 = - (x^{2} - 6 x + 9) = - {(x - 3)}^{2} \leq 0$

Nên $- x^{2} + 6 x - 9 = 0 \Leftrightarrow x = 3$

Chọn đáp án A

Câu 33:

Cho hai số $M = 2^{10}, N = 3^{10}$ . Khẳng định nào sau đây đúng ?

$A . M > N$

$B . N = M + 1$

$C . M = N$

$D . M < N$

Xem đáp án

$3^{10} > 2^{10} \Rightarrow N > M$

Chọn đáp án D

Câu 34:

Tính tích P các nghiệm của phương trình :

x^{2} - 7 x + 10 = 0

$A . P = - 10$

$B . P = 10$

$C . P = - 7$

$D . P = 7$

Xem đáp án

$x_{1} x_{2} = \frac{c}{a} = 10$

Chọn đáp án B

Câu 35:

Tính bán kính R của đường tròn ngoại tiếp tam giác đều ABC cạnh 2 cm

$A . R = 2 \sqrt{3} c m$

$B . R = \sqrt{3} c m$

$C . R = \frac{\sqrt{3}}{3} c m$

$D . R = \frac{2 \sqrt{3}}{3} c m$

Xem đáp án

$R = \frac{2}{3} A H = \frac{2}{3} . \frac{\sqrt{3}}{2} A B = \frac{2}{3} . \frac{\sqrt{3}}{2} .2 = \frac{2 \sqrt{3}}{3} (c m)$

Chọn đáp án D

Câu 36:

Trên đường tròn $(O; 6 c m)$ lấy ba điểm $A, B, C$ sao cho BC là đường trung trực của OA .Tính độ dài đoạn thẳng AB

$A . A B = 5 c m$

$B . A B = 3 c m$

$C . A B = 6 c m$

$D . A B = \sqrt{7} c m$

Xem đáp án

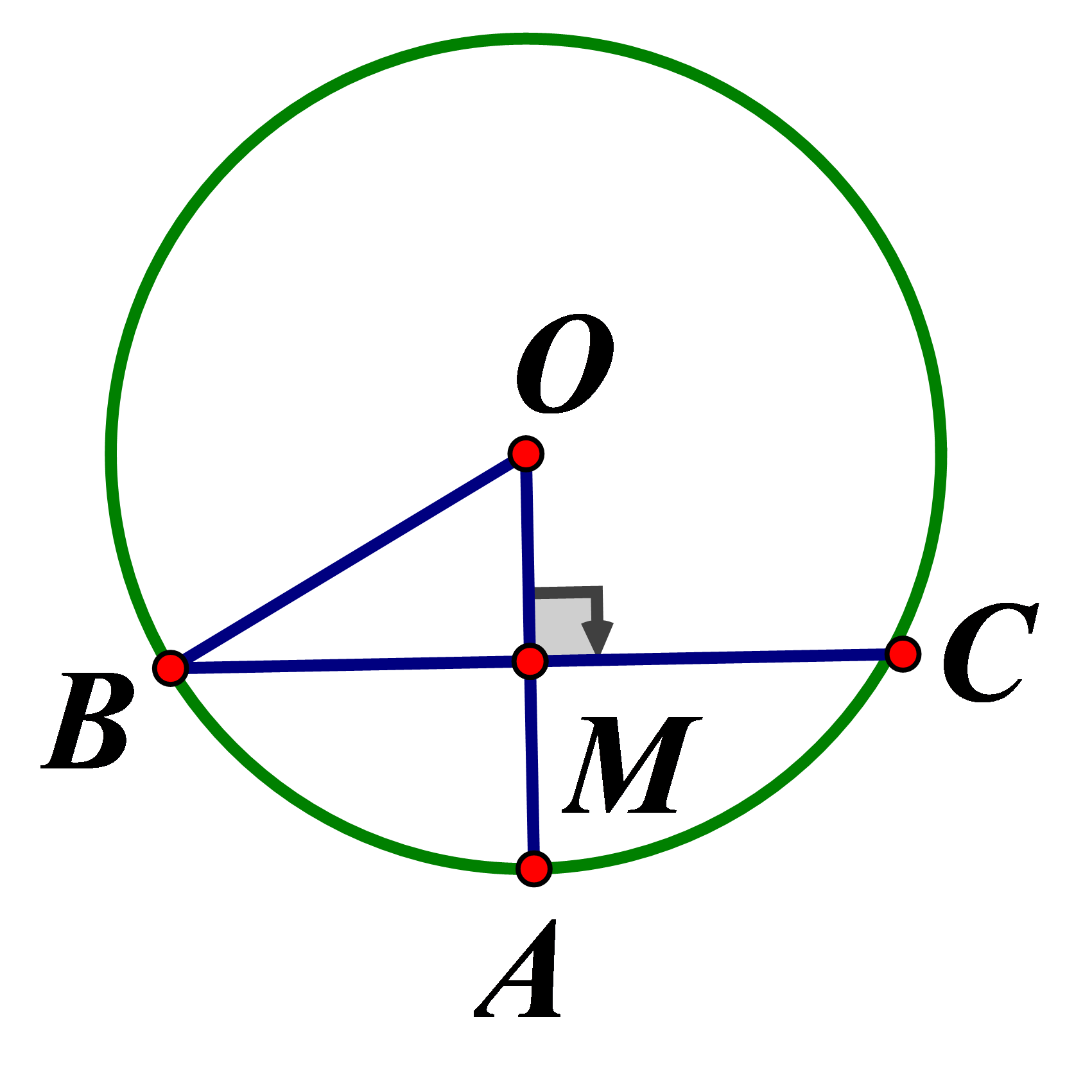
Gọi M là trung điểm $O A \Rightarrow O M = M A = \frac{R}{2} = \frac{6}{2} = 3 c m$

Do $O M ⊥ A B \Rightarrow M$ là trung điểm AB (tính chất đường kính dây cung)

Áp dụng định lý Pytago, Ta có :

$B M = \sqrt{O B^{2} - O M^{2}} = \sqrt{6^{2} - 3^{2}} = 3 \sqrt{3} (c m)$

\Rightarrow A B = \sqrt{B M^{2} + A M^{2}} = \sqrt{{(3 \sqrt{3})}^{2} + 3^{2}} = 6 (c m)

Chọn đáp án C

Câu 37:

Tìm điều kiện của x để đẳng thức $\sqrt{(x + 2) (x - 3)} = \sqrt{x + 2} . \sqrt{x - 3}$ đúng

$A . x \geq 3$

$B . x > 3$

$C . x \geq - 2$

$D . x > - 2$

Xem đáp án

đẳng thức $\sqrt{(x + 2) (x - 3)} = \sqrt{x + 2} . \sqrt{x - 3}$ đúng $\Leftrightarrow \{\begin{cases} x + 2 \geq 0 \\ x - 3 \geq 0 \end{cases} \Rightarrow x \geq 3$

Chọn đáp án A

Câu 38:

Kêt quả thống kê điểm kiểm tra học kỳ I môn toán của học sinh lớp thầy giáo lập được bảng tần số sau :

Điểm	4	5	6	7	8	9	10
Tần số	6	4	11	a	b	5	2	N=40

Biết điểm trung bình cộng là 6,65 Tính T=b-a

$A . T = 12$

$B . T = 5$

$C . T = 7$

$D . T = 2$

Xem đáp án

Ta có: $\begin{array}{l} \frac{4.6 + 5.4 + 6.11 + 7 a + 8 b + 9.5 + 10.2}{40} = 6, 65 \Rightarrow 7 a + 8 = 91 (2) \\ (1), (2) \Rightarrow \{\begin{cases} a + b = 12 \\ 7 a + 8 b = 91 \end{cases} \Leftrightarrow \{\begin{cases} a = 5 \\ b = 7 \end{cases} \Rightarrow T = b - a = 7 - 5 = 2 \end{array}$

Chọn đáp án D

Câu 39:

Cho phương trình $x^{2} - 2 (m - 2) x + m^{2} - 3 m = 0 (m$ là tham số). Tìm các giá trị của m để phương trình đã cho có hai nghiệm phân biệt $x_{1}, x_{2}$ thỏa mãn $x_{1}^{2} + x_{2}^{2} = 8$

$A . m = 1$

$B . m = - 4$

$C . m = - 1$

$D . m = 4$

Xem đáp án

Để phương trình có hai nghiệm thì $Δ' \geq 0$

$\Leftrightarrow {(m - 2)}^{2} - (m^{2} - 3) \geq 0 \Leftrightarrow - 4 m \geq - 7 \Leftrightarrow m \leq \frac{7}{4}$

Lúc đó, áp dụng Vi et ta có: $\{\begin{cases} x_{1} + x_{2} = 2 m - 4 \\ x_{1} x_{2} = m^{2} - 3 m \end{cases}$

$\begin{array}{l} x_{1}^{2} + x_{2}^{2} = 8 \Leftrightarrow {(x_{1} + x_{2})}^{2} - 2 x_{1} x_{2} = 8 \Leftrightarrow {(2 m - 4)}^{2} - 2 (m^{2} - 3 m) = 8 \\ \Leftrightarrow 2 m^{2} - 10 m + 8 = 0 \Leftrightarrow [\begin{array}{l} m = 1 (t m) \\ m = 4 (k t m) \end{array} \end{array}$

Chọn đáp án A

Câu 40:

Cắt mặt cầu (S) bằng một mặt phẳng đi qua tâm ta được mặt cắt là một hình tròn có chu vi bằng $4 π (c m)$ . Tính thể tích V của hình cầu (S)

$A . V = 32 π (c m^{3})$

$B . V = \frac{32 π}{3} (c m^{3})$

$C . V = \frac{16}{3} π (c m^{3})$

$D .16 π (c m^{3})$

Xem đáp án

$C = 2 π R = 4 π \Rightarrow R = 2 \Rightarrow V = \frac{4}{3} π R^{3} = \frac{4}{3} π {.2}^{3} = \frac{32 π}{3} (c m^{3})$

Chọn đáp án B

Câu 41:

Cho đường tròn

(O; R)

. Qua điểm A thuộc đường tròn, kẻ tiếp tuyến Ax trên đó lấy điểm B sao cho

O B = \sqrt{2} R, O B

cắt đường tròn tại C.Tính góc ở tâm tạo bởi hai bán kính OA,OC

$A {.90}^{0}$

$B {.105}^{0}$

$C {.35}^{0}$

$D .45 °$

Xem đáp án

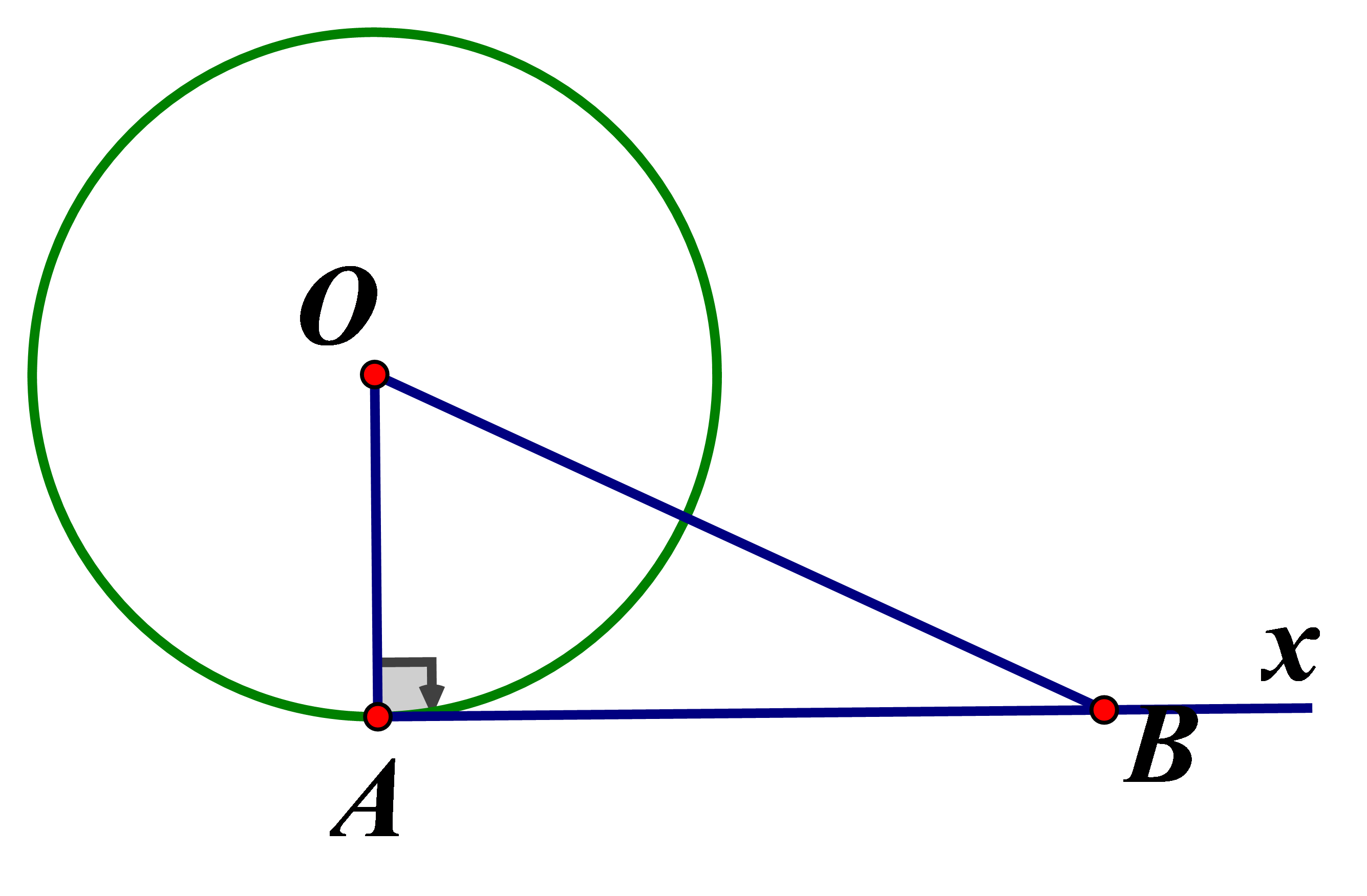
Ta có $\cos ∠ O = \frac{O A}{O B} = \frac{R}{R \sqrt{2}} = \frac{\sqrt{2}}{2} \Rightarrow ∠ O = 45 °$

Chọn đáp án D

Câu 42:

Một phòng họp có 360 ghế ngồi được sắp xếp thành từng dãy và số ghế của từng dãy đều bằng nhau. Vì cuộc họp có 400 đại biểu nên phải tăng thêm một dãy ghế và mỗi dãy ghế tăng thêm 1 ghế. Hỏi ban đầu trong phòng họp có bao nhiêu dãy ghế (biết rằng số dãy ghế ít hơn số ghế trên một dãy) ?

$A . 15 d ã y$

$B . 12 d ã y$

$C . 18 d ã y$

$D . 24 d ã y$

Xem đáp án

Gọi số dãy ghế trong phòng họp là x dãy $(x \in ℕ, x > 0)$

Ta có phương trình : $(x + 1) (\frac{360}{x} + 1) = 400 \Leftrightarrow [\begin{array}{l} x = 15 \\ x = 24 \end{array}$

Vì số ghế nhiều hơn số dãy nên x=15

Chọn đáp án A

Câu 43:

Cho tam giác ABC cân tại A, $B C = 12 c m .$ đường cao $A H = 4 c m .$ Tính bán kính R của đường tròn ngoại tiếp tam giác ABC

$A . R = 5, 5 (c m)$

$B . R = 6 (c m)$

$C . R = 7 (c m)$

$D . R = 6, 5 (c m)$

Xem đáp án

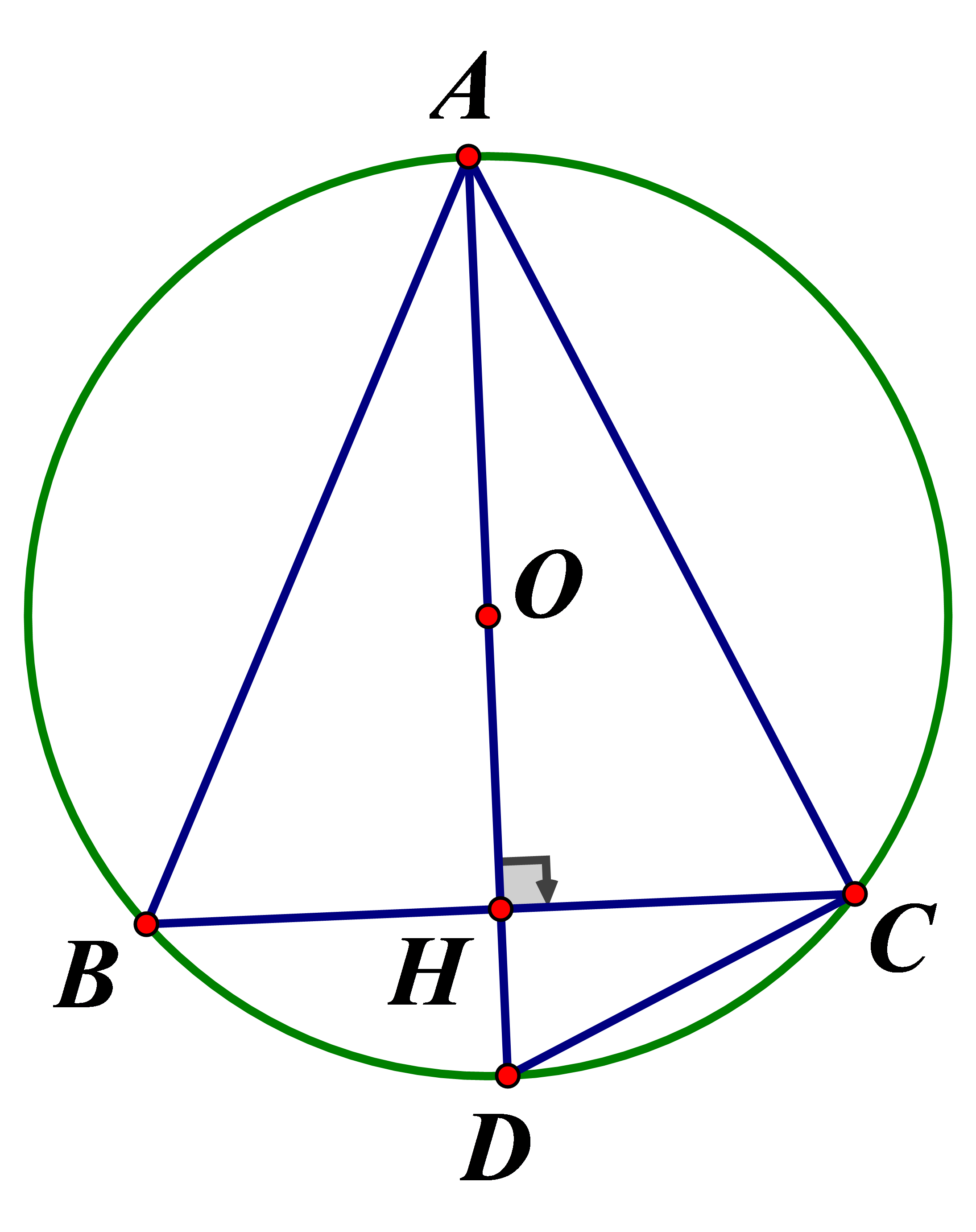
Gọi $(O)$ là tâm đường tròn ngoại tiếp $Δ A B C, D$ là giao điểm của AH và (O)

$Δ A B C$ cân tại A nên AH là đường cao đồng thời là đường trung trực, trung tuyến của cạnh $B C \Rightarrow A D$ là đường trung trực của BC

$\Rightarrow A D$ là đường kính của $(O) \Rightarrow C H = \frac{B C}{2} = 6 (c m)$

$Δ A C D$ nội tiếp đường tròn đường kính $A D \Rightarrow Δ A C D$ vuông tại C

Xét $Δ A C D$ vuông tại C ta có: $C H^{2} = A H . H D \Rightarrow H D = \frac{C H^{2}}{A H} = \frac{6^{2}}{4} = 9 (c m)$ $\Rightarrow A D = A H + H D = 9 + 4 = 13 \Rightarrow R = \frac{A D}{2} = \frac{13}{2} = 6, 5 (c m)$

Chọn đáp án D

Câu 44:

Nếu tăng chiều dài thêm 2(m) và tăng chiều rộng thêm 3(m) của một thửa ruộng hình chữ nhật thì diện tích tăng thêm $100 (m^{2}) .$ Nếu cùng giảm cả chiều dài và chiều rộng đi $2 (m)$ thì diện tích giảm đi $68 (m^{2})$ . Tính diện tích S của thửa ruộng ban đầu ?

$A . S = 306 (m^{2})$

$B . S = 308 (m^{2})$

$C . S = 310 (m^{2})$

$D . S = 304 (m^{2})$

Xem đáp án

Gọi $x, y$ lần lượt là chiều dài, chiều rộng ban đầu $(x > y > 2)$ .

Theo bài ta có phương trình : $\{\begin{cases} (x + 2) (y + 3) = x y + 100 \\ (x - 2) (y - 2) = x y - 68 \end{cases} \Leftrightarrow \{\begin{cases} 3 x + 2 y = 94 \\ - 2 x - 2 y = - 72 \end{cases} \Leftrightarrow \{\begin{cases} x = 22 \\ y = 14 \end{cases} \Rightarrow S = 308 (c m^{2})$

Chọn đáp án B

Câu 45:

Một số tự nhiên a khi chia cho 7 thì dư 5, chia cho 13 thì dư 4. Hỏi số khi chia cho 91 thì dư là bao nhiêu ?

$A .71$

$B .20$

$C .9$

$D .82$

Xem đáp án

Theo đề ta có : $a = 7 m + 5$ và $a = 13 n + 4 (m, n \in ℕ)$ , cộng thêm 9 vào a ta được $a + 9 = 7 m + 14 = 7 (m + 2) ⋮ 7 \Rightarrow a + 9 ⋮ 7$

Và $a + 9 = 13 n + 13 = 13 (n + 1) ⋮ 13 \Rightarrow a + 9 ⋮ 13$

Mà $(7, 13) = 1 \Rightarrow a + 9 ⋮ 7.13 \Leftrightarrow a + 9 ⋮ 91 \Rightarrow a + 9 = 91 k (k \in ℕ)$

Hay $a = 91 k - 9 = 91 k - 91 + 9 = 91 (k - 1) + 82,$ do đó dư 82

Chọn đáp án D

Câu 46:

Cho tam giác ABC có $A B = 10 (c m), B C = 1 (c m) .$ Tính diện tích S của tam giác ABC biết độ dài cạnh AC là một số tự nhiên (tính theo đơn vị cm)

$A . S = \frac{\sqrt{399}}{4} (c m^{2})$

$B . \frac{\sqrt{399}}{2} (c m^{2})$

$C . \frac{\sqrt{399}}{6} (c m^{2})$

$D . \frac{\sqrt{399}}{8} (c m^{2})$

Xem đáp án

Áp dụng bất đẳng thức tam giác $\Rightarrow 10 - 1 < A C < 10 + 1 \Rightarrow A C = 10 (A C \in ℕ)$

Vậy $A B = A C = 10 c m, B C = 1 c m$ . Áp dụng hệ thức Hê rông với là nửa chu vi ta có:

$S = \sqrt{p (p - A B) (p - A C) (p - B C)} = \frac{\sqrt{399}}{4}$ .Chọn đáp án A

Câu 47:

Cho đường tròn

(O; 15 c m)

và dây AB=18cm vẽ dây CD song song và có khoảng cách đến AB bằng 21cm.Tính độ dài dây CD

$A . C D = 10 (c m)$

$B . C D = 5 (c m)$

$C . C D = 24 (c m)$

$D . C D = 12 (c m)$

Xem đáp án

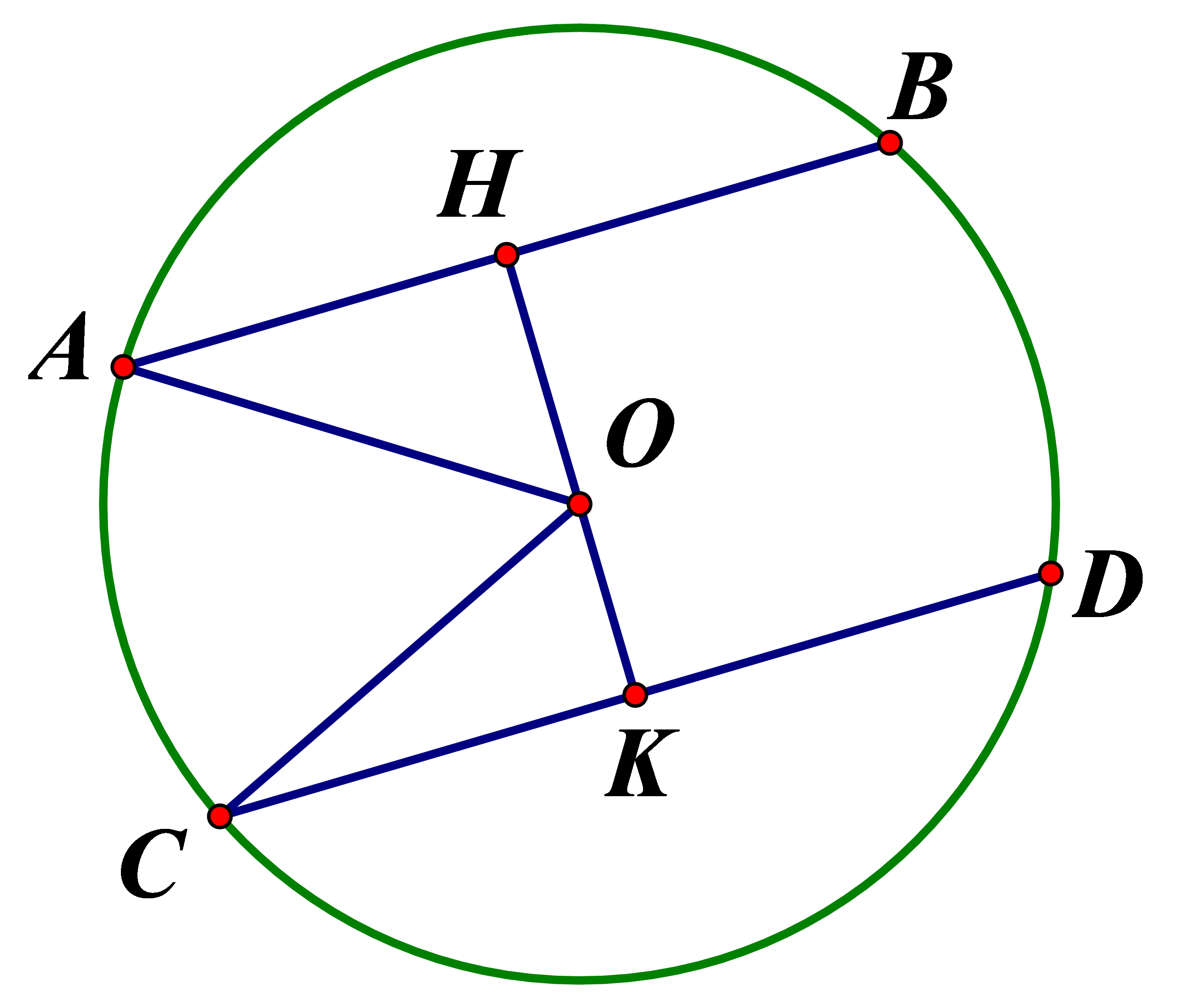
Gọi H là trung điểm AB. Hạ $H K ⊥ C D \Rightarrow K$ là trung điểm CD (đường kính – dây cung)

Áp dụng định lý Pytago

$\Rightarrow O H = \sqrt{O A^{2} - A H^{2}} = \sqrt{15^{2} - 9^{2}} = 12 \Rightarrow O K = H K - O H = 21 - 12 = 9 (c m)$

$C K = \sqrt{C O^{2} - O K^{2}} = \sqrt{15^{2} - 9^{2}} = 12 \Rightarrow C D = 2 C K = 12.2 = 24 (c m)$

Chọn đáp án C

Câu 48:

Kết quả rút gọn biểu thức $K = (\frac{\sqrt{a}}{\sqrt{a} - 1} - \frac{1}{a - \sqrt{a}}) : (\frac{1}{\sqrt{a} + 1} + \frac{2}{a - 1})$ $(\begin{array}{l} a > 0 \\ a \neq 1 \end{array})$ có dạng $\frac{m . a + n}{\sqrt{a}} .$ Tính giá trị của $2 m + 3 n$

$A .2 m + 3 n = 4$

$B .2 m + 3 n = - 1$

$C .2 m + 3 n = - 4$

$D .2 m + 3 n = 1$

Xem đáp án

$\begin{array}{l} K = (\frac{\sqrt{a}}{\sqrt{a} - 1} - \frac{1}{a - \sqrt{a}}) : (\frac{1}{\sqrt{a} + 1} + \frac{2}{a - 1}) = \frac{a - 1}{\sqrt{a} (\sqrt{a} - 1)} : \frac{\sqrt{a} - 1 + 2}{a - 1} \\ = \frac{a - 1}{\sqrt{a} (\sqrt{a} - 1)} . \frac{a - 1}{\sqrt{a} + 1} = \frac{{(a - 1)}^{2}}{(a - 1) \sqrt{a}} = \frac{a - 1}{\sqrt{a}} \Rightarrow \{\begin{cases} m = 1 \\ n = - 1 \end{cases} \Rightarrow 2 m + 3 n = 2 - 3 = - 1 \end{array}$

Chọn đáp án B

Câu 49:

Có bao nhiêu giá trị nguyên dương của n để đa thức $7 x^{n - 1} y^{5} - 5 x^{3} y^{4}$ chia hết cho đơn thức $x^{2} y^{n}$

$A .2$

$B .1$

$C .3$

$D . V ô s ố$

Xem đáp án

để đa thức $7 x^{n - 1} y^{5} - 5 x^{3} y^{4}$ chia hết cho đơn thức $x^{2} y^{n}$

$\Rightarrow \{\begin{cases} n - 1 \geq 2 \\ n \leq 4 \end{cases} \Rightarrow 3 \leq n \leq 4$ $\Rightarrow n \in \{3; 4\}$ . Có 2 giá trị

Chọn đáp án A

Câu 50:

Cho góc $α (0^{0} < α < 90^{0}),$ biết $\cos α - \sin α = \frac{1}{3} .$ Tính giá trị của biểu thức $T = \sin α . \cos α$

$A . T = \frac{3}{2}$

$B . T = \frac{2}{3}$

$C . T = \frac{4}{9}$

$D . T = \frac{9}{4}$

Xem đáp án

$\begin{array}{l} \cos α - \sin α = \frac{1}{3} \Leftrightarrow {(\cos α - \sin α)}^{2} = \frac{1}{9} \Leftrightarrow \cos^{2} α + \sin^{2} α - 2 \cos α \sin α = \frac{1}{9} \\ \Leftrightarrow 1 - 2 \cos α \sin α = \frac{1}{9} \Rightarrow \cos α \sin α = \frac{1 - \frac{1}{9}}{2} = \frac{4}{9} \end{array}$

Chọn đáp án C