50 câu hỏi trắc nghiệm thuộc Bộ 30 đề thi vào 10 môn Toán có lời giải chi tiết (Đề 14)

Câu 1:

Cặp số nào sau đây là nghiệm của hệ phương trình

\{\begin{cases} 4 x + 5 y = 3 \\ x - 3 y = 5 \end{cases} ?

$A . (- 2; - 1)$

$B . (2; - 1)$

$C . (3; 1)$

$D . (2; 1)$

Xem đáp án

Ấn $M o d e - 5 - 1$ (giải hệ phương trình bậc nhất 1 ẩn ) được đáp án

Vậy chọn đáp án B

Câu 2:

Tìm số tự nhiên $n (n \in ℕ *)$ biết rằng:

$A . n = 12$

$B . n = 14$

$C . n = 16$

$D . n = 18$

Xem đáp án

Số số hạng : $(2 n - 2) : 2 + 1 = n$ nên tổng $(2 n + 2) . n : 2 = n (n + 1)$

Ta có $(n + 1) n = 156 = 13.12 \Rightarrow n = 12$

Chọn đáp án A

Câu 3:

Xác định tất cả các giá trị của để ba đường thẳng $y = \frac{\sqrt{6}}{4} k x + \sqrt{53}; y = (k - 1) x + \sqrt{53}; y = \sqrt{7} k^{2} x + \sqrt{53}$ đồng quy tại một điểm trên trục tung

$A . [\begin{array}{l} k = 1 \\ k = 4 \end{array}$

$B . [\begin{array}{l} k = 0 \\ k = 3 \end{array}$

$C . [\begin{array}{l} k = 1 \\ k = 2 \end{array}$

$D . k \in ℝ s a o c h o k \neq 0; k \neq 1$

Xem đáp án

Vì ba hàm số đều có $b = \sqrt{53}$ nên cả 3 đều cắt trục tung tại $(0; \sqrt{53})$ nẻn ta có hệ:

$\{\begin{cases} \sqrt{53} = \frac{\sqrt{6}}{4} k .0 + \sqrt{53} \\ \sqrt{53} = (k - 1) .0 + \sqrt{53} \\ \sqrt{53} = \sqrt{7} . k^{2} .0 + \sqrt{53} \end{cases} \Leftrightarrow \{\begin{cases} 0 k = 0 \\ 0 k = 0 \\ 0 k = 0 \end{cases} \Rightarrow k \in ℝ / k \neq 1, k \neq 0$

Chọn đáp án D

Câu 4:

Cho tam giác có $A B = 20 c m, B C = 12 c m, C A = 16 c m .$ Tính chu vi của đường tròn nội tiếp tam giác đã cho

$A .8 π c m$

$B .13 π c m$

$C .20 π c m$

$D .16 π c m$

Xem đáp án

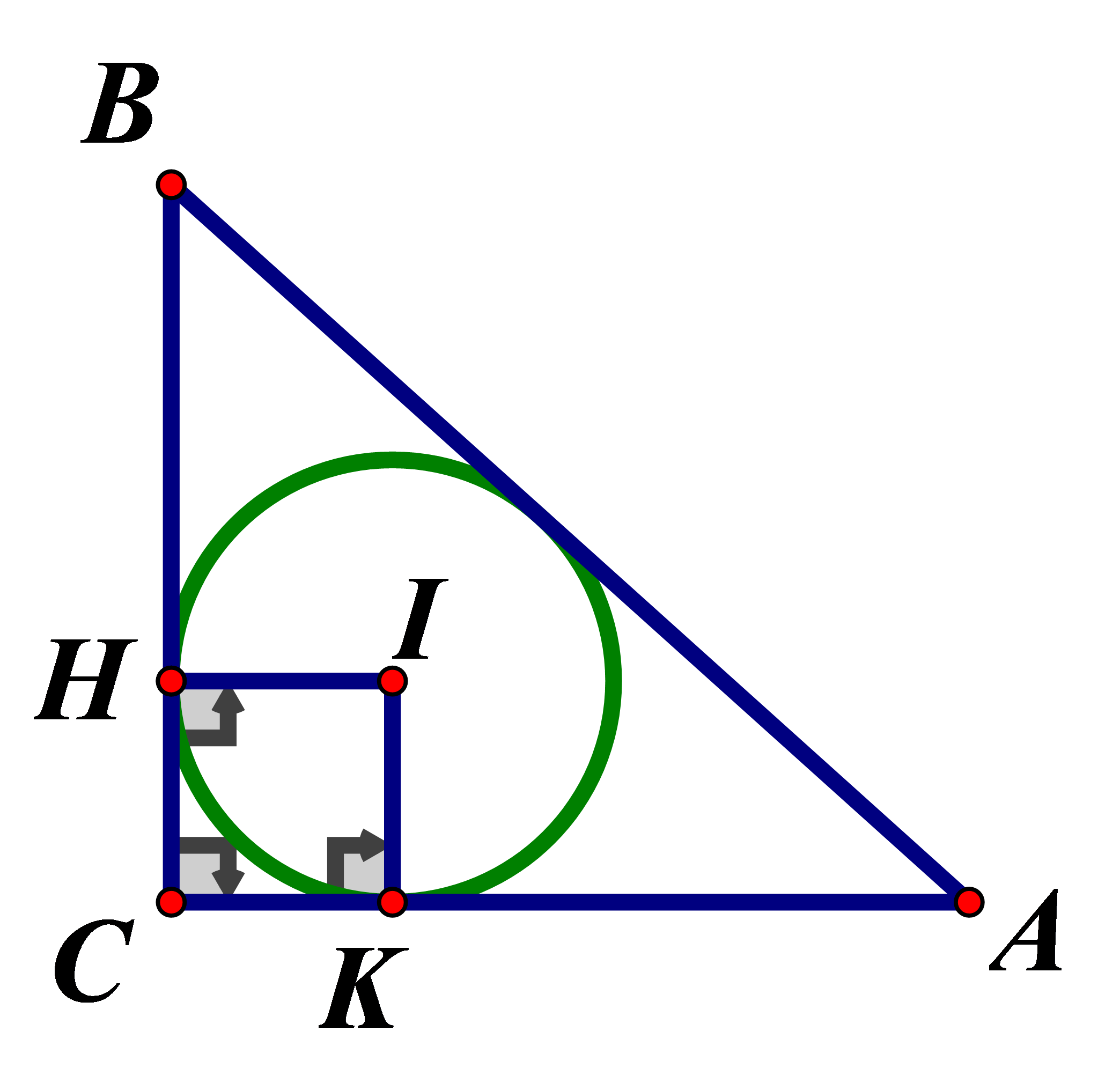
Vì $A B^{2} = B C^{2} + A C^{2} \Rightarrow Δ A B C$ vuông tại C

Vẽ hình vuông $C H I K$ (với I là tâm đường tròn nội tiếp, $I H ⊥ B C, I K ⊥ A C)$

Ta có: $r = C H = \frac{C A + C B - A B}{2} = 4$ nên chu vi: $2 π .4 = 8 π$

Chọn đáp án A

Câu 5:

Đường thẳng $y = (k + 1) x + 3$ cắt trục hoành tại điểm có hoành độ bằng 1. Giá trị của là k:

$A . k = - 4$

$B . k = 4$

$C . k = 1$

$D . k = - 1$

Xem đáp án

$y = (k + 1) x + 3 (k \neq - 1) (d)$ cắt trục hoành tại điểm có hoành độ bằng $1 \Rightarrow \{\begin{cases} x_{0} = 1 \\ y_{0} = 0 \end{cases} (*)$

Thay $(*)$ và $(d) \Rightarrow 0 = (k + 1) .1 + 3 \Leftrightarrow 0 = k + 1 + 3 \Leftrightarrow k = - 4 (t m)$

Chọn đáp án A

Câu 6:

Biểu thức nào sau đây có dạng bình phương một hiệu

$A .1 - 2 x^{2} + 2 x^{4}$

$B . y^{2} - 2 y + 2$

$C .4 a^{2} - 4 a + 1$

$D .9 - 6 b + 3 b^{2}$

Xem đáp án

Ta thấy $4 a^{2} - 4 a + 1 = {(2 a - 1)}^{2}$ . Chọn đáp án C

Câu 7:

Cho tam giác ABC có chu vi bằng 30cm và diện tích bằng $45 c m^{2} .$ Vẽ đường tròn $(O)$ nội tiếp tam giác $A B C .$ Bán kính của đường tròn đó bằng:

$A .6 c m$

$B .3 c m$

$C .8 c m$

$D .5 c m$

Xem đáp án

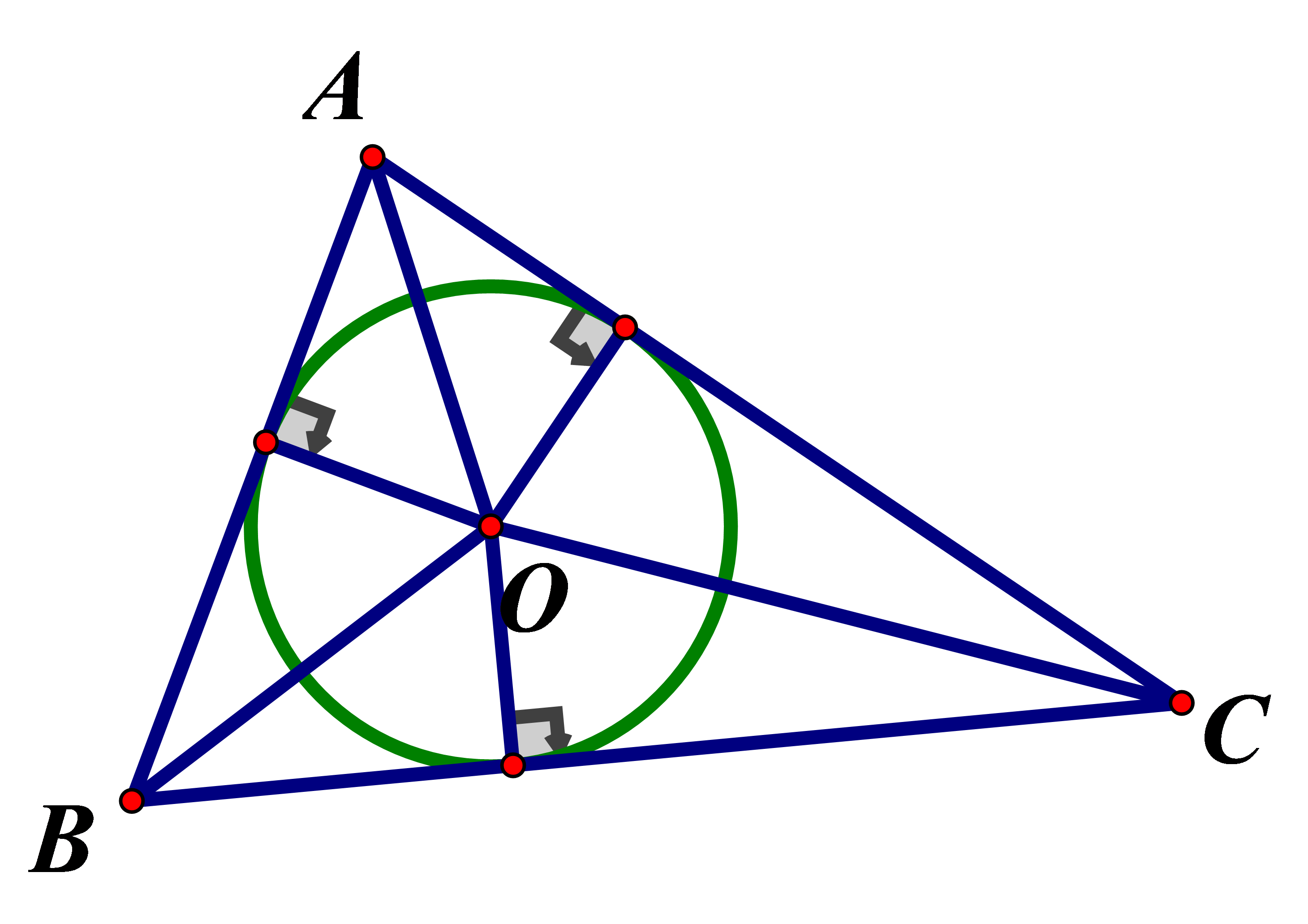
Gọi r là bán kính đường tròn nội tiếp $Δ A B C$ . Ta có:

$\begin{array}{l} S_{A B C} = S_{A O B} + S_{A O C} + S_{B O C} \\ = \frac{1}{2} A B . r + \frac{1}{2} A C . r + \frac{1}{2} B C . r = \frac{1}{2} (A B + B C + C A) r = \frac{1}{2} P_{A B C} . r (P : c h u v i) \\ \Leftrightarrow 45 = \frac{1}{2} .30. r \Leftrightarrow r = 3 c m \end{array}$

Chon đáp án B

Câu 8:

Bộ ba đoạn thẳng có độ dài nào sau đây có thể là độ dài ba cạnh của một tam giác vuông ?

$A .6 c m, 8 c m, 10 c m$

$B .2 c m, 3 c m, 5 c m$

$C .6 c m, 9 c m, 14 c m$

$D .4 c m, 9 c m, 12 c m$

Xem đáp án

Ta xét $a^{2} = b^{2} + c^{2}$ với a là cạnh lớn nhất (định lý Pytago đảo)

Được : $10^{2} = 100 = 6^{2} + 8^{2}$

Chọn đáp án A

Câu 9:

Kết quả của phép tính $\sqrt{{(1 - \sqrt{7})}^{2}}$ là :

$A .1 - \sqrt{7}$

$B .1 + \sqrt{7}$

$C . \sqrt{7} - 1$

$D . - 6$

Xem đáp án

$\sqrt{{(1 - \sqrt{7})}^{2}} = |1 - \sqrt{7}| = \sqrt{7} - 1$ (do nên câu C đúng, $\sqrt{7} > 1)$ chọn đáp án C

Câu 10:

Một dây AB của đường tròn (O) có độ dài 12cm .Biết khoảng cách từ tâm O đến dây AB là 8cm .Bán kính của đường tròn đó bằng:

$A .2 d m$

$B .10 d m$

$C .1 d m$

$D .2 c m$

Xem đáp án

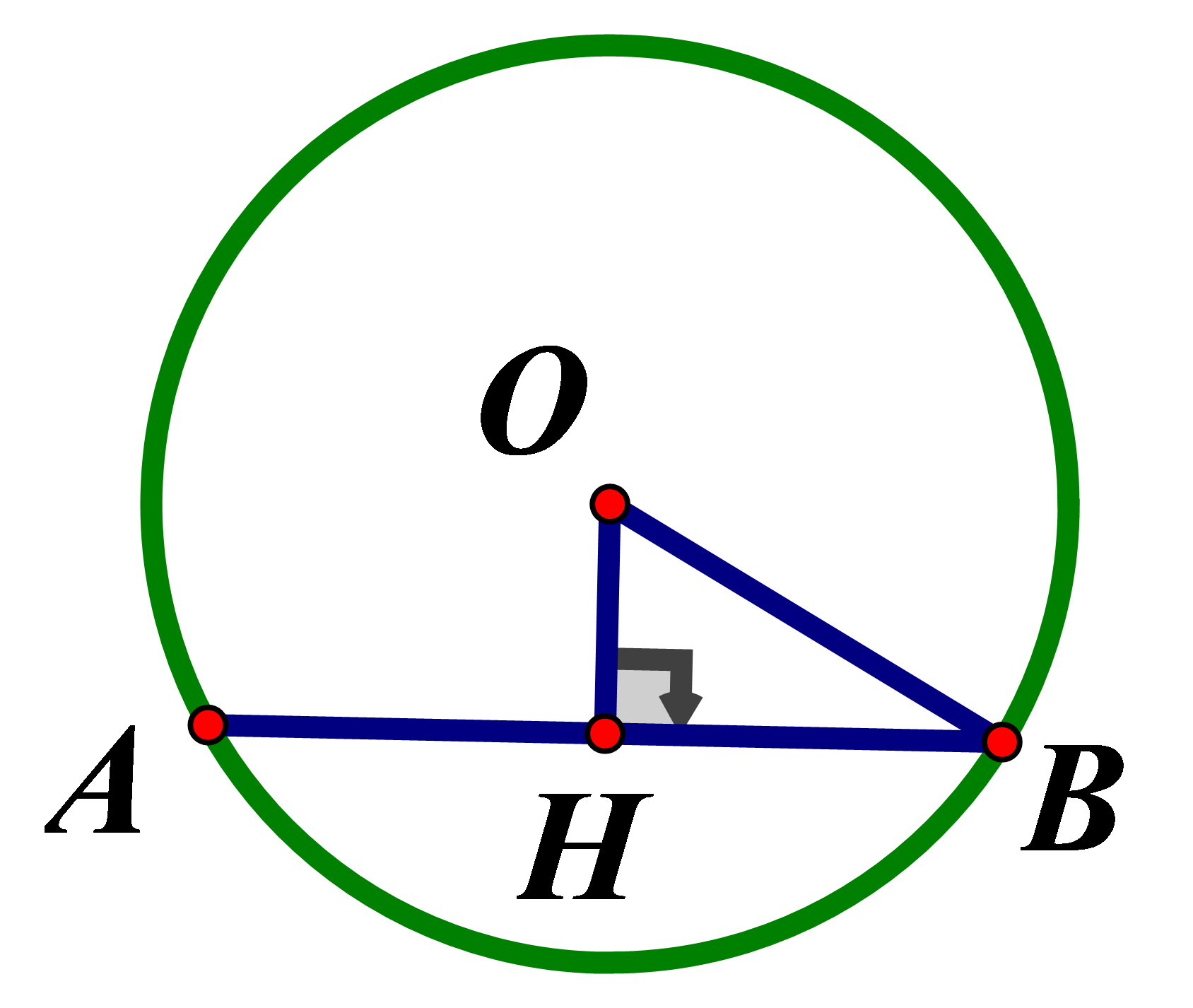
Hạ $O H ⊥ A B \Rightarrow H$ là trung điểm của AB (đường kính dây cung)

Nên $H B = \frac{A B}{2} = \frac{12}{2} = 6 (c m)$

$Δ O H B$ vuông tại H nên $O B = \sqrt{O H^{2} + H B^{2}}$ (định lý Pytago)

$= \sqrt{8^{2} + 6^{2}} = 10 (c m) = 1 d m$

Chọn đáp án C

Câu 11:

Cho tam giác ABC vuông tại A có $A B = 9 c m, A C = 12 c m .$ Đường cao AH có độ dài là :

$A . A H = 7, 2 c m$

$B . A H = 3, 6 c m$

$C . A H = 6, 5 c m$

$D . A H = 2, 4 c m$

Xem đáp án

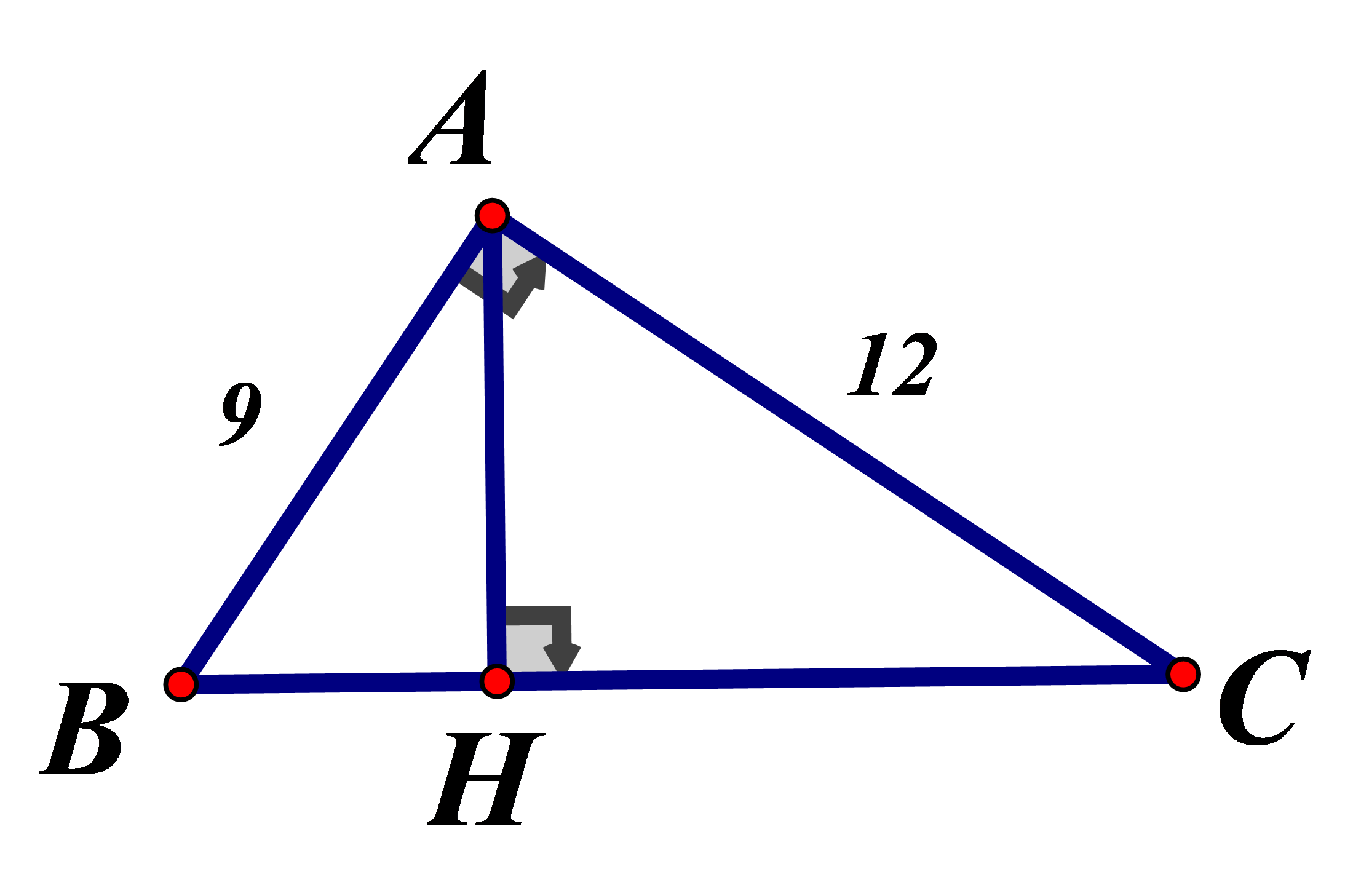
Áp dụng hệ thức lượng vào $Δ A B C$ vuông tại A, đường cao AH

$\Rightarrow \frac{1}{A H^{2}} = \frac{1}{9^{2}} + \frac{1}{12^{2}} = \frac{25}{1296} \Rightarrow A H = \sqrt{\frac{1296}{25}} = 7, 2 (c m)$

Chọn đáp án A

Câu 12:

Phương trình $\frac{2 x - 1}{x - 1} + \frac{x}{(x - 1) (x - 2)} = \frac{6 x - 2}{x - 2}$ có nghiệm là :

$A . [\begin{array}{l} x = 0 \\ x = 1 \end{array}$

$B . x = 0$

$C . x = 1$

$D . x = 2$

Xem đáp án

$\begin{array}{l} \frac{2 x - 1}{x - 1} + \frac{x}{(x - 1) (x - 2)} = \frac{6 x - 2}{x - 2} (\begin{array}{l} x \neq 1 \\ x \neq 2 \end{array}) \Leftrightarrow \frac{(2 x - 1) (x - 2) + x}{(x - 1) (x - 2)} = \frac{(6 x - 2) (x - 1)}{(x - 1) (x - 2)} \\ \Rightarrow 2 x^{2} - 5 x + 2 + x = 6 x^{2} - 8 x + 2 \Leftrightarrow 4 x^{2} - 4 x = 0 \\ \Leftrightarrow x (x - 1) = 0 \Leftrightarrow [\begin{array}{l} x = 0 (t m) \\ x = 1 (k t m) \end{array} \Rightarrow S = \{0\} \end{array}$

Chọn đáp án B.

Câu 13:

Cho tam giác ABC biết $A B = 9 c m, A C = 1 c m, B C = a (c m)$ với $a \in ℕ .$ Khi đó giá trị của a là :

$A . a = 9$

$B . a = 5$

$C . a = 10$

$D . a = 2$

Xem đáp án

Áp dụng bất đẳng thức tam giác ta có:

$A B - A C < B C < A B + A C$ hay $9 - 1 > a < 9 + 1 \Leftrightarrow 8 < a < 10 \Rightarrow a = 9$ (do $a \in ℕ)$

Chọn đáp án A

Câu 14:

Giá trị x nguyên thỏa mãn ${(- \frac{3}{4})}^{3 x - 1} = \frac{256}{81}$

$A . x = - 2$

$B . x = 1$

$C . x = - 1$

$D . x = 2$

Xem đáp án

$\begin{array}{l} {(- \frac{3}{4})}^{3 x - 1} = \frac{256}{81} \Leftrightarrow {(- \frac{3}{4})}^{3 x - 1} = {(- \frac{3}{4})}^{- 4} \\ \Rightarrow 3 x - 1 = - 4 \Leftrightarrow x = - 1 \end{array}$

Chọn đáp án C

Câu 15:

Hai số x và y thỏa mãn $7 x = 3 y; x - y = 16$ là :

$A . x = - 12, y = - 28$

$B . x = 12, y = 28$

$C . x = - 2, y = - 28$

$D . x = - 12, y = - 8$

Xem đáp án

$7 x = 3 y \Rightarrow \frac{x}{3} = \frac{y}{7}$ . Áp dụng tính chất dãy tỉ số bằng nhau:

$\Rightarrow \frac{x}{3} = \frac{y}{7} = \frac{x - y}{3 - 7} = \frac{16}{- 4} = - 4$ $\Rightarrow \frac{x}{3} = - 4 \Rightarrow x = - 12, \frac{y}{7} = - 4 \Rightarrow y = - 28$

Chọn đáp án A

Câu 16:

Đồ thị hàm số $y = a x + b$ đi qua điểm $M (1; \sqrt{3} + 5)$ và song song với đường thẳng $y = \sqrt{3} x$ là :

$A . y = - \sqrt{3} x + 5$

$B . y = \sqrt{3} x + 1$

$C . y = x + \sqrt{3} + 5$

$D . y = \sqrt{3} x + 5$

Xem đáp án

Đường thẳng $y = a x + b$ song song với đường thẳng $y = \sqrt{3} x$ $\Rightarrow \{\begin{cases} a = \sqrt{3} \\ b \neq 0 \end{cases}$

Đường thẳng $y = \sqrt{3} x + b$ đi qua điểm $M (1; \sqrt{3} + 5)$

$\Rightarrow \sqrt{3} + 5 = \sqrt{3} .1 + b \Leftrightarrow b = 5 (t m)$

Vậy $y = \sqrt{3} x + 5$ . Chọn đáp án D

Câu 17:

Cho tam giác $A B C, A D$ là phân giác trong của góc $B A C .$ Vẽ $D E / / A B (E \in A C) .$ Biết $A B = 4 c m, A C = 6 c m .$ Tính DE

$A . D E = \frac{2}{3} c m$

$B . D E = 2 c m$

$C . D E = 2, 4 c m$

$D . D E = 1, 5 c m$

Xem đáp án

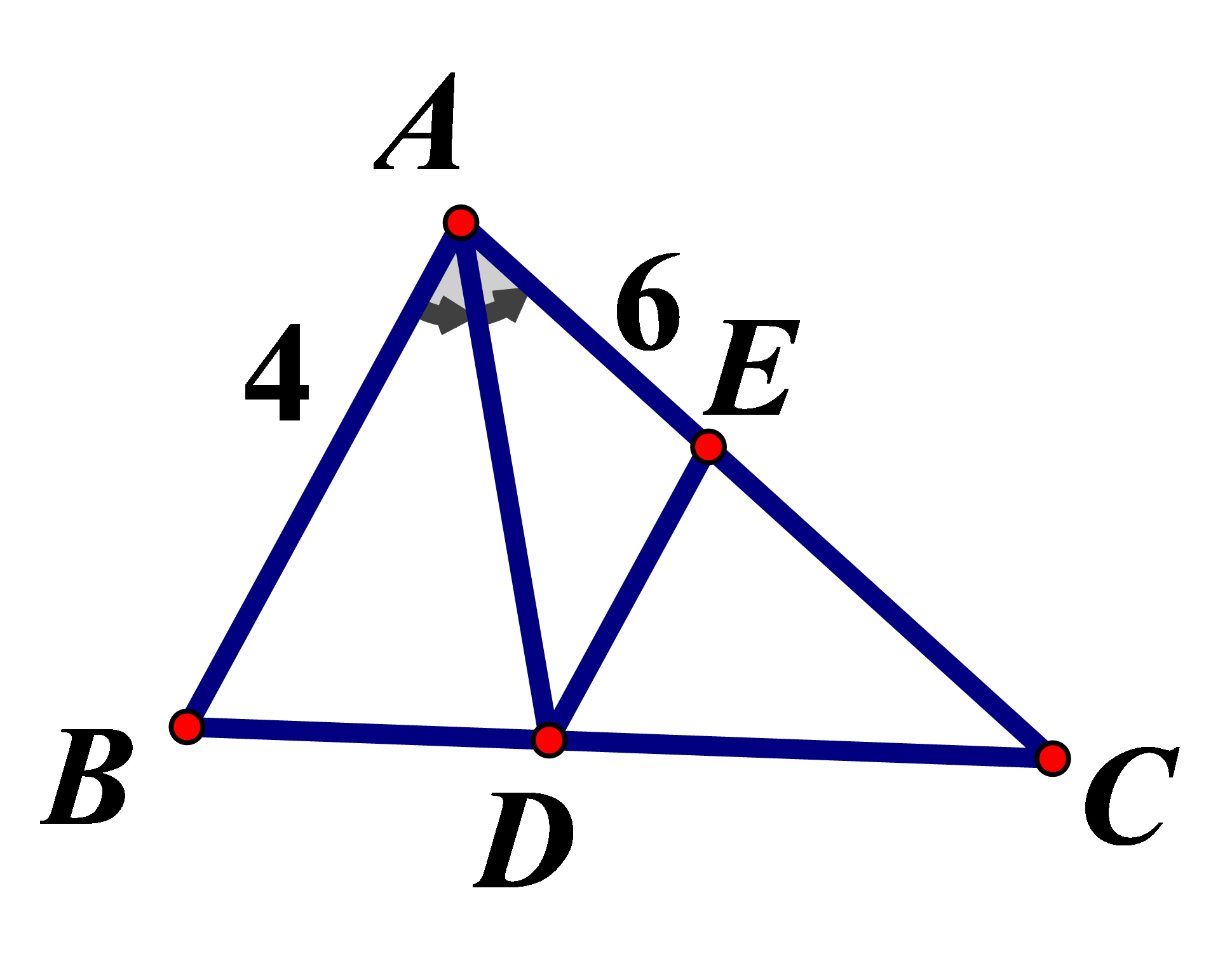
Ta có: $D E / / A B \Rightarrow \frac{D E}{A B} = \frac{C D}{B C}$ (định lý Ta let)

$\Rightarrow \frac{D E}{A B} = \frac{C D}{B D + D C}$ $\Leftrightarrow \frac{A B}{D E} = \frac{B D + D C}{D C}$ hay $\frac{4}{D E} = \frac{B D}{D C} + 1 (1)$

Lại có AD là phân giác trong của $∠ B A C \Rightarrow \frac{B D}{D C} = \frac{A B}{A C} = \frac{4}{6} (2)$

Từ (1) và (2) ta có: $\frac{4}{D E} = \frac{4}{6} + 1 \Rightarrow D E = 2, 4 c m$

Chon đáp án C

Câu 18:

Đồ thị hàm số

y = a x (a < 0)

nằm trong những góc phần tư :

$A . (I I), (I I I)$

$B . (I), (I V)$

$C . (I I), (I V)$

$D . (I), (I I I)$

Xem đáp án

Vì $a < 0$ , ta dặt $a = - 1 \Rightarrow y = - x$ . Vẽ đồ thị

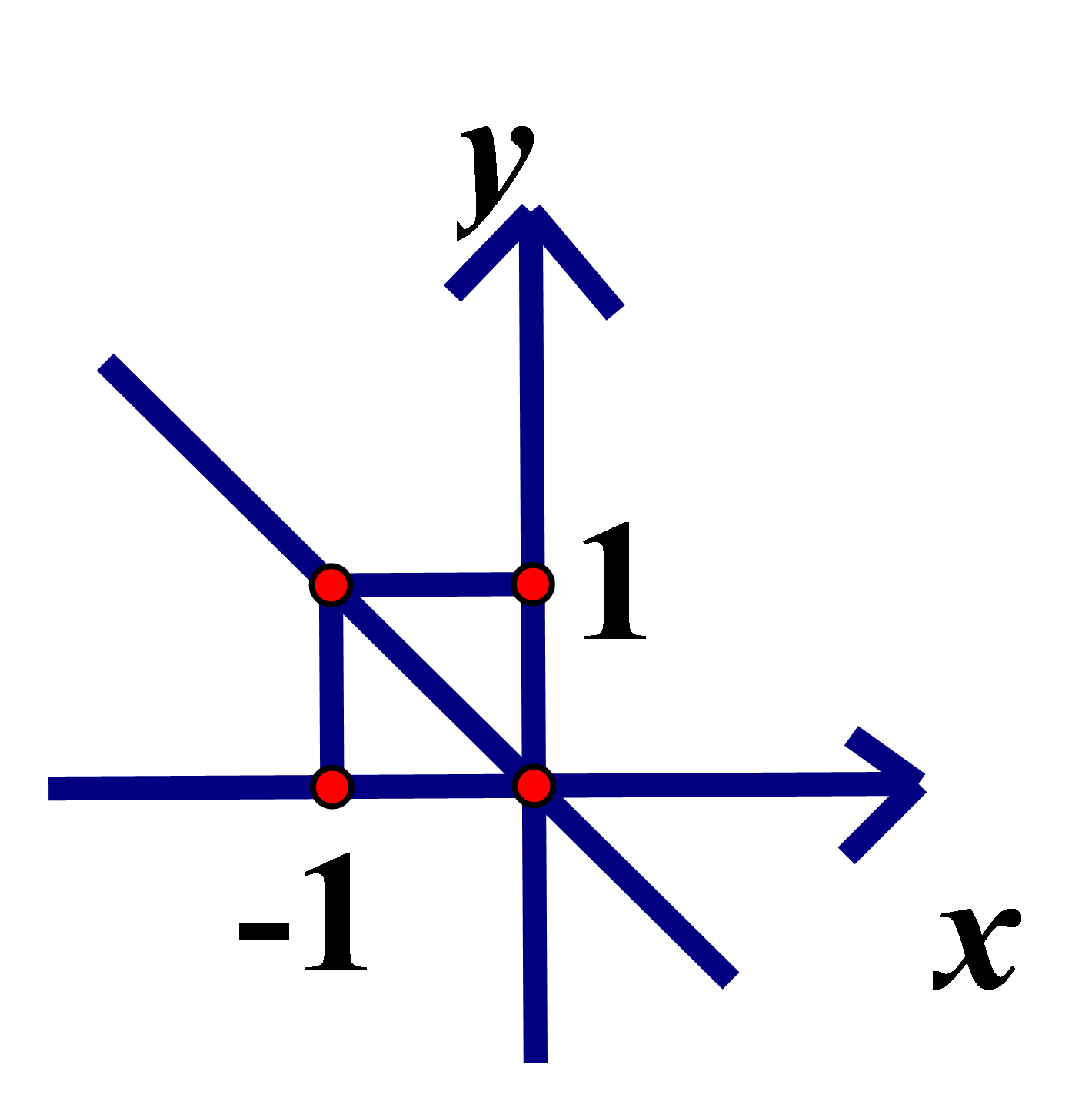
$\Rightarrow y = - x$ nằm góc phần tư thứ (II) và (IV). Chọn đáp án C

Câu 19:

Khẳng định nào sau đây là sai ?

$A . \sin 45^{0} = \cos 45^{0}$

$B . \sin 20^{0} = \sin 70^{0}$

$C . \sin 30^{0} = \frac{1}{2}$

$D . \tan 45^{0} = \cot 45^{0}$

Xem đáp án

Câu sai là $\sin 20 ° = \sin 70 °$ . Chọn B

Câu 20:

Tích của $2009.2010$ có bao nhiêu ước ?

$A .75$

$B .90$

$C .96$

$D .81$

Xem đáp án

$2009.2010 = 7^{2} .41.2.3.5.67$ . Nên số ước là :

$(2 + 1) (1 + 1) (1 + 1) (1 + 1) (1 + 1) (1 + 1) = 96$ (ước)

Chọn đáp án C

Câu 21:

Tổng khoảng cách từ một đỉnh của hình vuông cạnh bằng 2cm tới trung điểm các cạnh hình vuông là :

$A .2 \sqrt{5} c m$

$B .2 + 2 \sqrt{5} c m$

$C .2 + \sqrt{3} c m$

$D .2 + 2 \sqrt{3} c m$

Xem đáp án

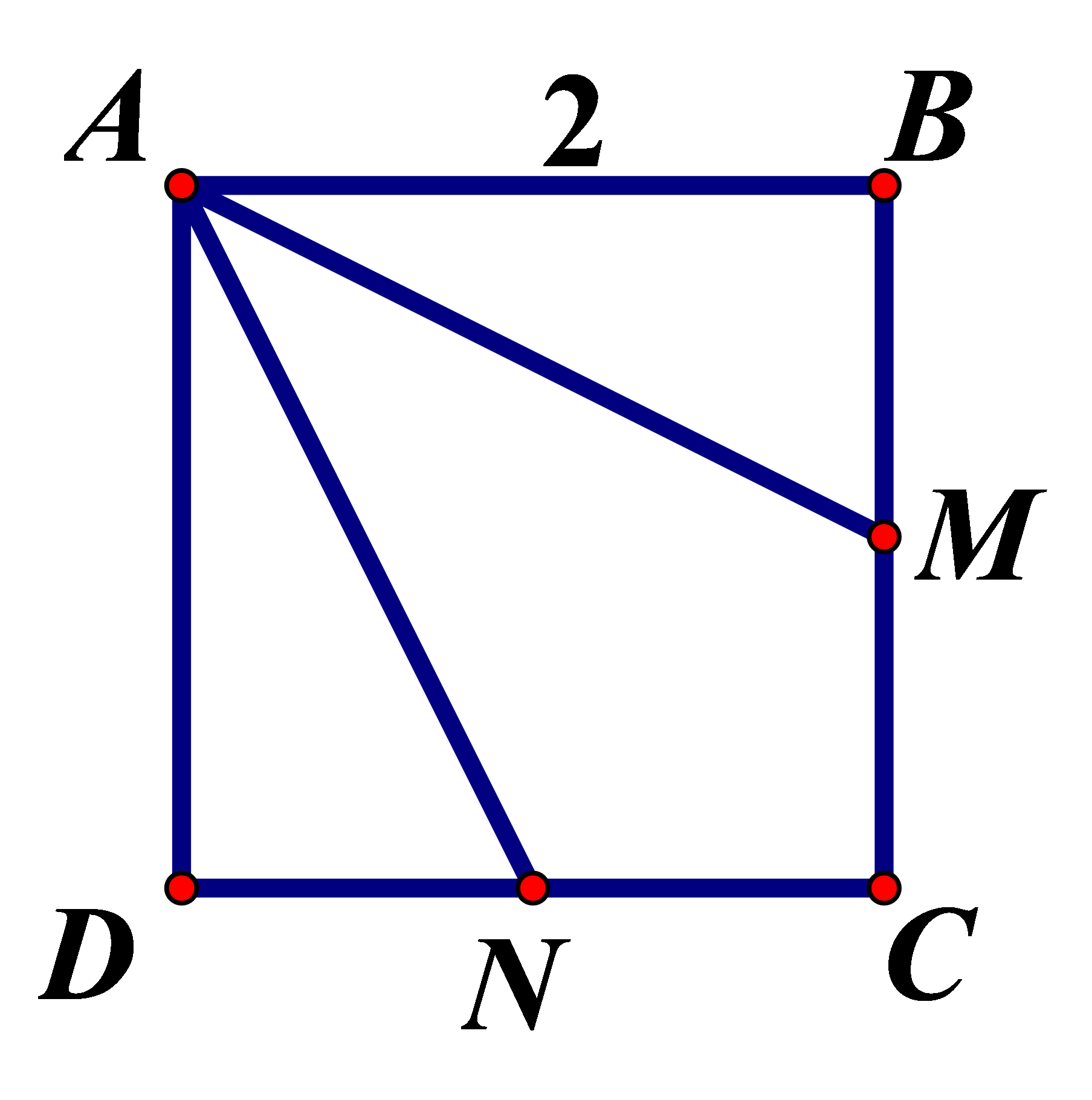
Áp dụng định lý Pytago ta có:

$A M = A N = \sqrt{1^{2} + 2^{2}} = \sqrt{5}$ . Vậy tổng cần tìm $= 1 + 1 + 2 \sqrt{5} = 2 + 2 \sqrt{5}$

Chọn đáp án B

Câu 22:

Cho $(O; 15 c m)$ và dây $A B = 24 c m .$ Một tiếp tuyến của đường tròn song song với AB cắt các tia OA,OB theo thứ tự ở $E, F .$ Tính EF

$A . E F = 42 c m$

$B . E F = 36 c m$

$C . E F = 40 c m$

$D . E F = 38 c m$

Xem đáp án

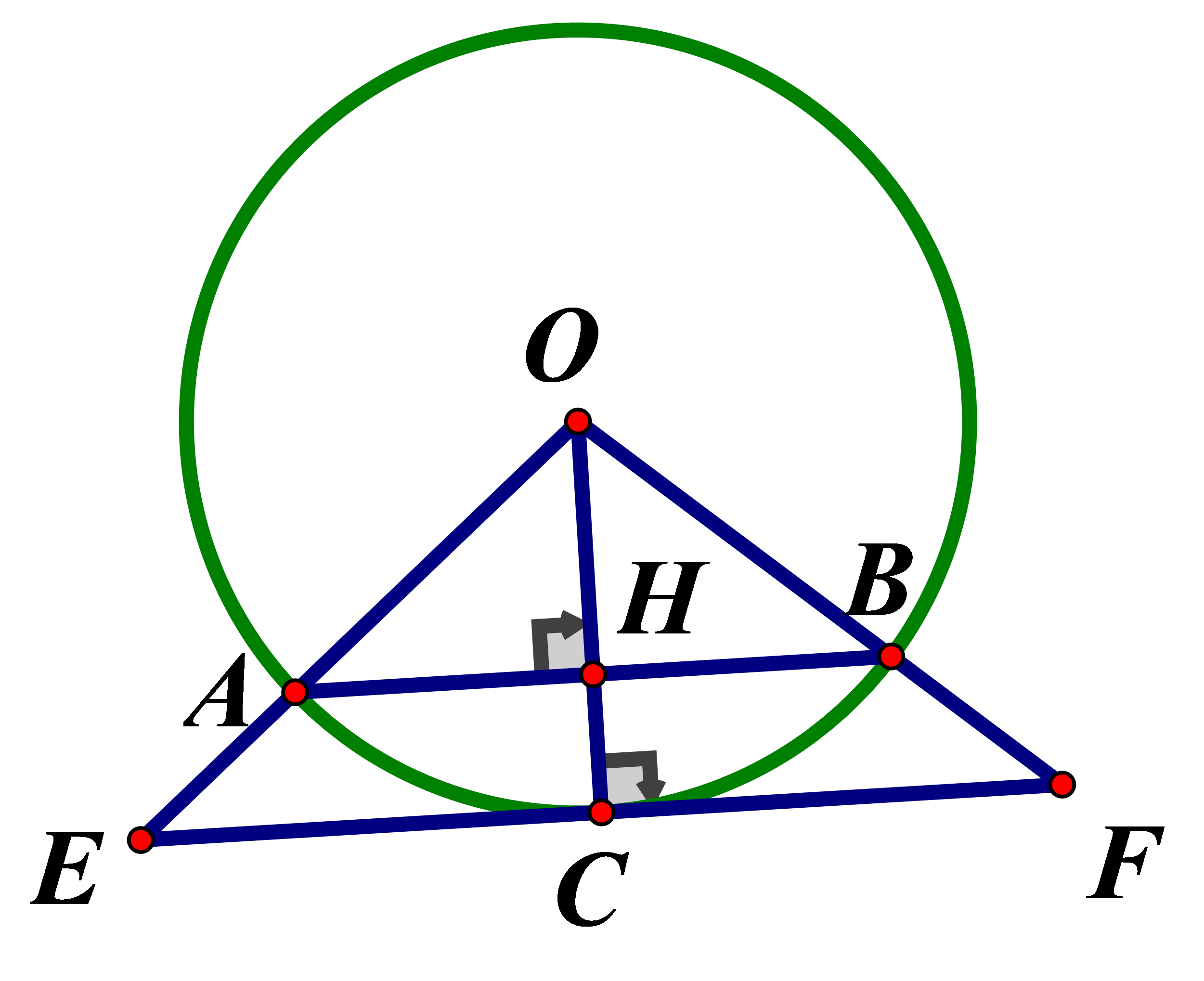
Gọi C là tiếp điểm của với đường tròn (O),H là giao điểm của OC và AB

Ta có $O C ⊥ E F$ (EF là tiếp tuyến của đường tròn (O))

Mà $A B / / E F (g t) \Rightarrow O C ⊥ A B$ tại H $\Rightarrow H$ là trung điểm của AB (đường kính – dây cung) $\Rightarrow H B = H A = \frac{A B}{2} = \frac{24}{2} = 12 (c m)$

Áp dụng định lý Pytago vào tam giác OHB vuông tại H, ta có:

$O H = \sqrt{O B^{2} - H B^{2}} = \sqrt{15^{2} - 12^{2}} = 9 (c m)$

$Δ O C F$ có $H B / / C F (H \in A B, C \in E F)$ , theo định lý Ta let ta có: $\frac{O H}{O C} = \frac{O B}{O F} (1)$

$Δ O E F$ có $A B / / E F \Rightarrow \frac{A B}{E F} = \frac{O B}{O F}$ (định lý ta let) (2)

Từ (1) và (2) suy ra $\frac{A B}{E F} = \frac{O H}{O C}$ , thay số

$\Rightarrow \frac{24}{E F} = \frac{9}{15} \Rightarrow E F = \frac{15.24}{9} = 40 (c m)$

Chọn đáp án C.

Câu 23:

Cho đường tròn $(O; 3 c m)$ . Tâm O của đường tròn cách dây AB là 1cm. Độ dài dây AB là :

$A . A B = 2 \sqrt{2} c m$

$B . A B = 4 \sqrt{2} c m$

$C . A B = 2 c m$

$D . A B = 3 \sqrt{2} c m$

Xem đáp án

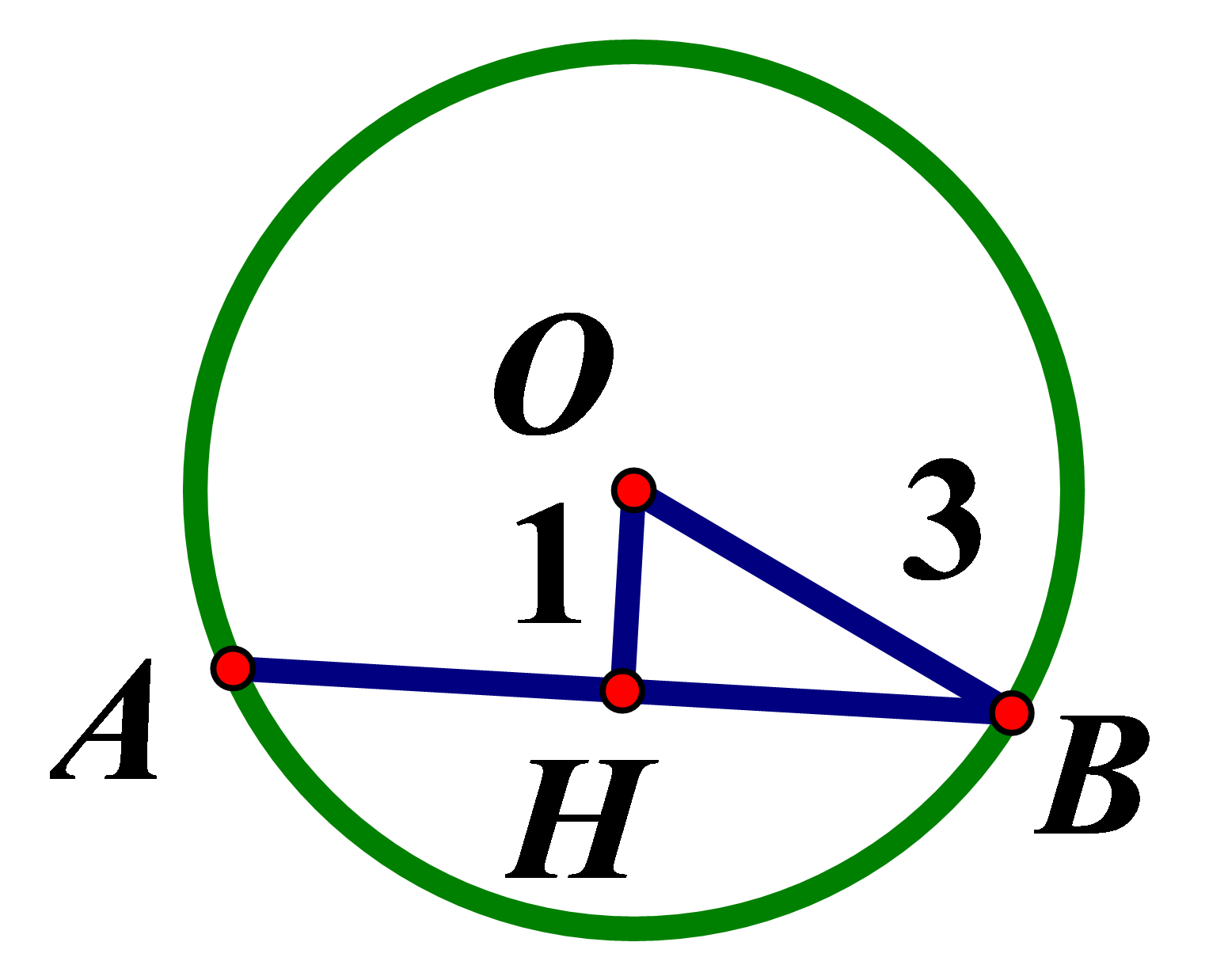
Hạ $O H ⊥ A B \Rightarrow H$ à trung điểm AB (đường kính dây cung)

$Δ O H B$ vuông tại H, theo định lý Pytago ta có:

$H B = \sqrt{O B^{2} - O H^{2}} = \sqrt{3^{2} - 1^{2}} = 2 \sqrt{2} (c m)$

$\Rightarrow A B = 2 H B = 2.2 \sqrt{2} = 4 \sqrt{2} (c m)$

Chọn đáp án B

Câu 24:

Nghiệm của phương trình $\sqrt{x + 1} = x - 1$ là :

$A . x = 0$

$B . x = 1$

$C . x = 3$

$D . x = 2$

Xem đáp án

$\sqrt{x + 1} = x - 1 (x > 1)$ . Bình phương 2 vế:

$\Rightarrow x + 1 = x^{2} - 2 x + 1 \Leftrightarrow x^{2} - 3 x = 0 \Leftrightarrow [\begin{array}{l} x = 0 (k t m) \\ x = 3 (t m) \end{array}$

Vậy chọn đáp án C

Câu 25:

Một cái thang dài 6m được đặt tạo với mặt đất một góc $60^{0} .$ Khi đó chân thang cách tường bao nhiêu mét ?

$A .1, 4 m$

$B .3, 2 c m$

$C .3 c m$

$D .2, 8 c m$

Xem đáp án

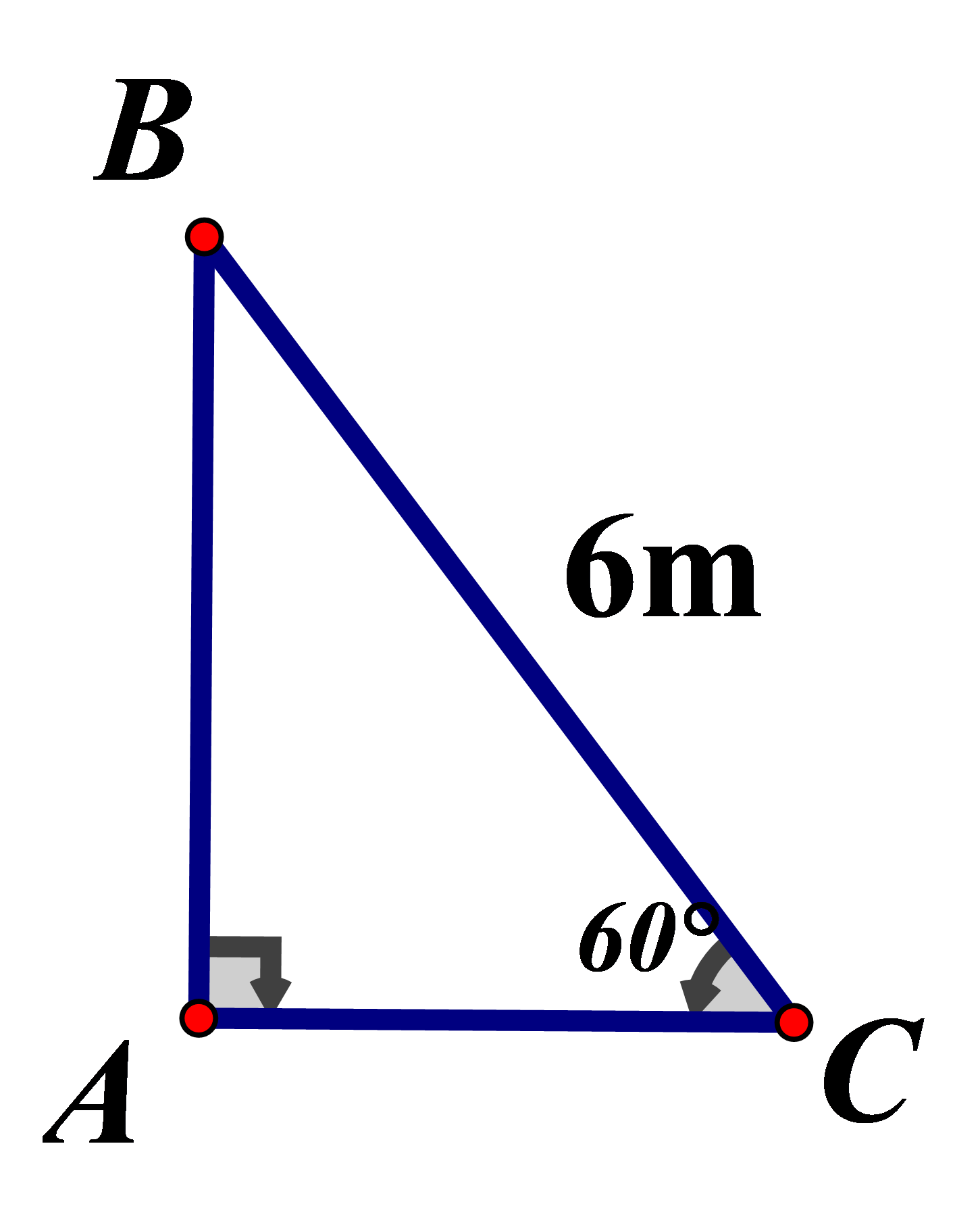
Khoảng cách cần tìm là AC. Ta có:

$\cos 60^{0} = \frac{A C}{B C} \Rightarrow A C = B C . \cos 60^{0} = 6. \cos 60^{0} = 3 (m)$

Chọn đáp án C

Câu 26:

Hàm số $y = (m - 3) x + 4$ đồng biến khi

$A . m < - 3$

$B . m > 3$

$C . m > - 3$

$D . m < 3$

Xem đáp án

$y = (m - 3) x + 4$ đồng biến khi $m - 3 > 0 \Leftrightarrow m > 3$

Chọn đáp án B

Câu 27:

Có 16 tờ tiền loại 2000 đồng,5000 đồng và 10000 đồng. Trị giá mỗi loại tiền trên đều bằng nhau. Hỏi loại tiền đồng có bao nhiêu tờ ?

$A .6$

$B .4$

$C .10$

$D .2$

Xem đáp án

Gọi $x, y, z$ lần lượt là số tờ tiền $2000, 5000, 10 000$

Nên ta có: $\{\begin{cases} x + y + z = 16 \\ 2 x = 5 y = 10 z \Rightarrow \frac{x}{5} = \frac{y}{2} = \frac{z}{1} \end{cases}$ . Áp dụng tính chất dãy ti số bằng nhau:

$\Rightarrow \frac{x}{5} = \frac{y}{2} = \frac{z}{1} = \frac{x + y + z}{5 + 2 + 1} = \frac{16}{8} = 2$ $\Rightarrow \frac{y}{2} = 2 \Leftrightarrow y = 4.$

Chọn đáp án B

Câu 28:

Cho hai đường thẳng $m^{2} x - y = m^{2} + 2 m$ và $(m + 1) x - 2 y = m - 1.$ Biết hai đường thẳng cắt nhau tại $A (3; 4) .$ Giá trị của m là :

$A . m = 3$

$B . m = - 1$

$C . m = 2$

$D . m = 0$

Xem đáp án

Vì $A (3; 4)$ đều thuộc 2 đồ thị

$\Rightarrow \{\begin{cases} 3 m^{2} - 4 = m^{2} + 2 m \\ (m + 1) .3 - 2.4 = m - 1 \end{cases} \Leftrightarrow \{\begin{cases} 2 m^{2} - 2 m - 4 = 0 \\ 3 m + 3 - 8 = m - 1 \end{cases} \Leftrightarrow \{\begin{cases} m^{2} - m - 2 = 0 \\ 2 m = 4 \end{cases} \Leftrightarrow m = 2$

Chọn đáp án C

Câu 29:

Cho tam giác ABC cân tại A nội tiếp đường tròn (O) tia AO cắt cung nhỏ $\overset{⏜}{B C}$ tại D biết số đo cung nhỏ $\overset{⏜}{B C}$ bằng $100^{0} .$ Tính số đo góc $∠ C O D ?$

$A . ∠ C O D = 100^{0}$

$B . ∠ C O D = 25^{0}$

$C . ∠ C O D = 50^{0}$

$D . ∠ C O D = 130^{0}$

Xem đáp án

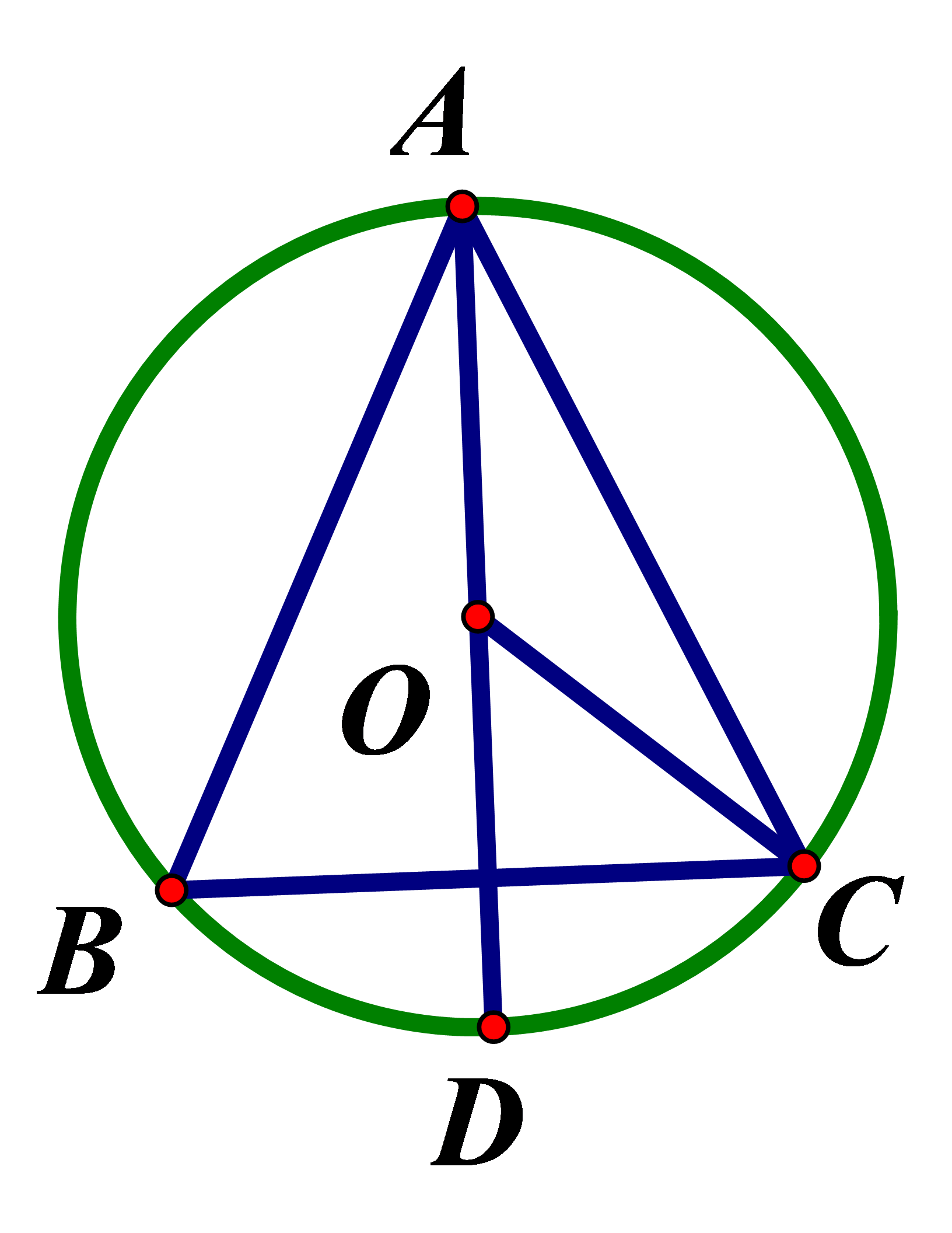
Vì $s d \overset{⏜}{B C}$ nhỏ $= 100^{0} \Rightarrow s d \overset{⏜}{D C} = \frac{1}{2} s d \overset{⏜}{B C}$ (vì AD là trung tuyến cũng là phân giác nên $s d \overset{⏜}{B D} = s d \overset{⏜}{D C})$ nên $s d \overset{⏜}{D C} = \frac{100^{0}}{2} = 50^{0}$

$∠ D O C$ là góc ở tâm nên $∠ C O D = s d \overset{⏜}{D C} = 50^{0} .$ Chọn đáp án C

Câu 30:

Đường thẳng đi qua hai điểm $O (0; 0)$ và $A (1; \sqrt{3})$ chứa đồ thị hàm số nào dưới đây ?

$A . y = \sqrt{3} x$

$B . y = x + \sqrt{3}$

$C . y = 2 x + 3$

$D . y = \sqrt{3} x + 1$

Xem đáp án

Vì đường thẳng qua điểm $(0; 0)$ nên có dạng $y = a x$

Vì đường thẳng $y = a x$ qua $(1; \sqrt{3}) \Rightarrow 1. a = \sqrt{3} \Rightarrow a = \sqrt{3} \Rightarrow y = \sqrt{3} x$

Chọn đáp án A

Câu 31:

Cho $(O; 10 c m)$ đường kính AB .Gọi T là trung điểm của OA.Tính bán kính r của đường tròn tiếp xúc với AB tại T và tiếp xúc với (O)

$A . r = \frac{13}{8} c m$

$B . r = \frac{15}{8} c m$

$C . r = \frac{13}{4} c m$

$D . r = \frac{15}{4} c m$

Xem đáp án

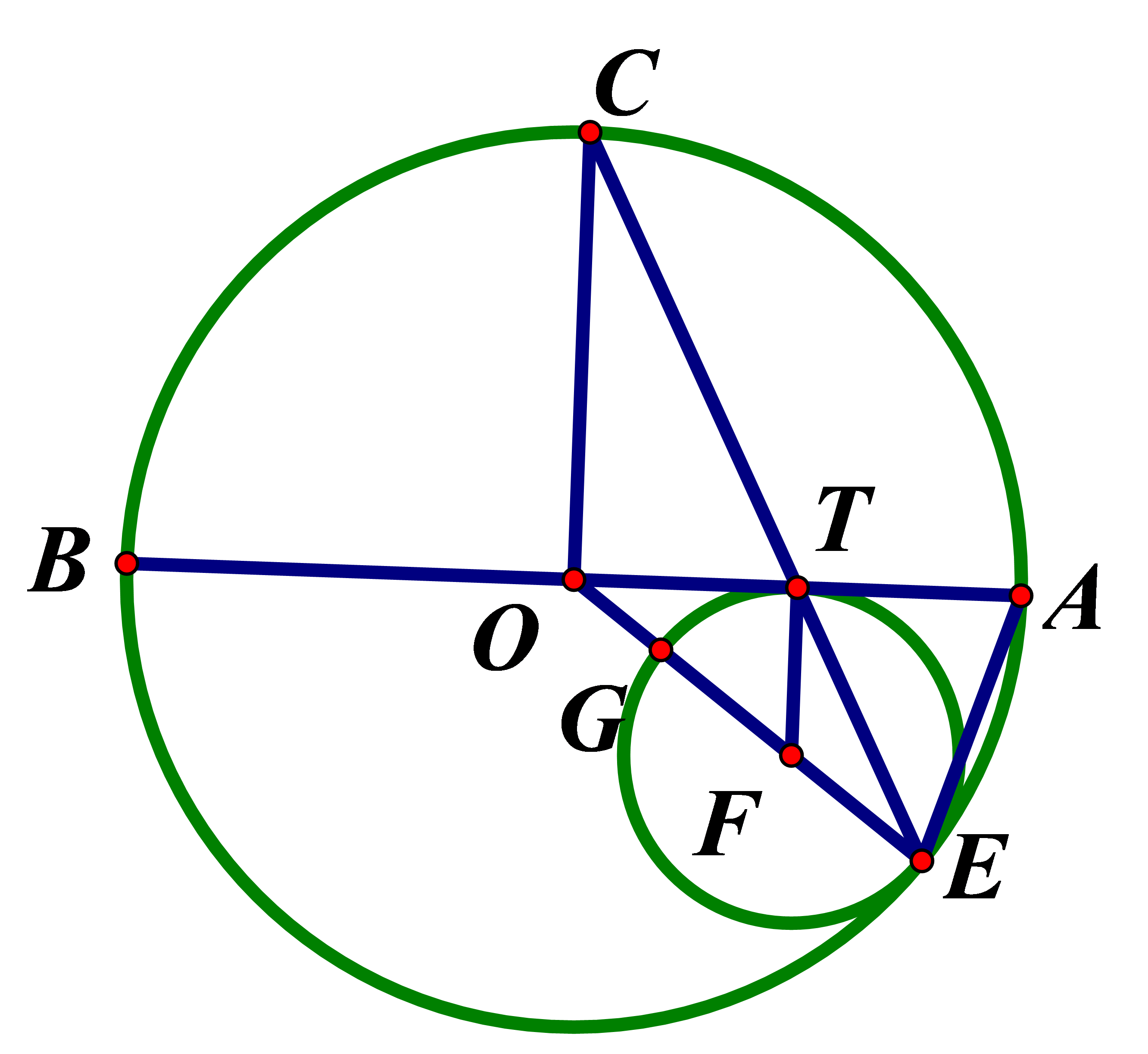
Gọi C là điểm chính giữa cung $A B . C T$ cắt (O) tại điểm thứ hai là E.OE cắt đường tròn tại F. Đường tròn $(F; F T)$ là đường tròn cần tìm .

Gọi G là giao điểm thứ hai của OE và đường tròn (F) Khi đó :

$O E . O G = O T^{2} = 25 \Rightarrow O G = 2.5 \Rightarrow F G = \frac{10 - 2, 5}{2} = \frac{15}{4} (c m)$

Chọn đáp án D.

Câu 32:

Trục căn thức của biểu thức : $\frac{a - 2 \sqrt{a}}{\sqrt{a} - 2} (a \geq 0)$ ta được kết quả :

$A . \sqrt{a}$

$C .2 \sqrt{a}$

$D .1$

Xem đáp án

$\frac{a - 2 \sqrt{a}}{\sqrt{a} - 2} = \frac{\sqrt{a} (\sqrt{a} - 2)}{\sqrt{a} - 2} = \sqrt{a} (a \geq 0)$

Chọn đáp án A

Câu 33:

Cho $Δ A B C$ vuông tại A có $A B = 3 c m, A C = 4 c m,$ đường cao AH và đường trung tuyến AM.Khi đó độ dài HM là bao nhiêu ?

$A . H M = \frac{9}{5} c m$

$B . H M = \frac{7}{10} c m$

$C . H M = \frac{43}{10} c m$

$D . H M = \frac{5}{2} c m$

Xem đáp án

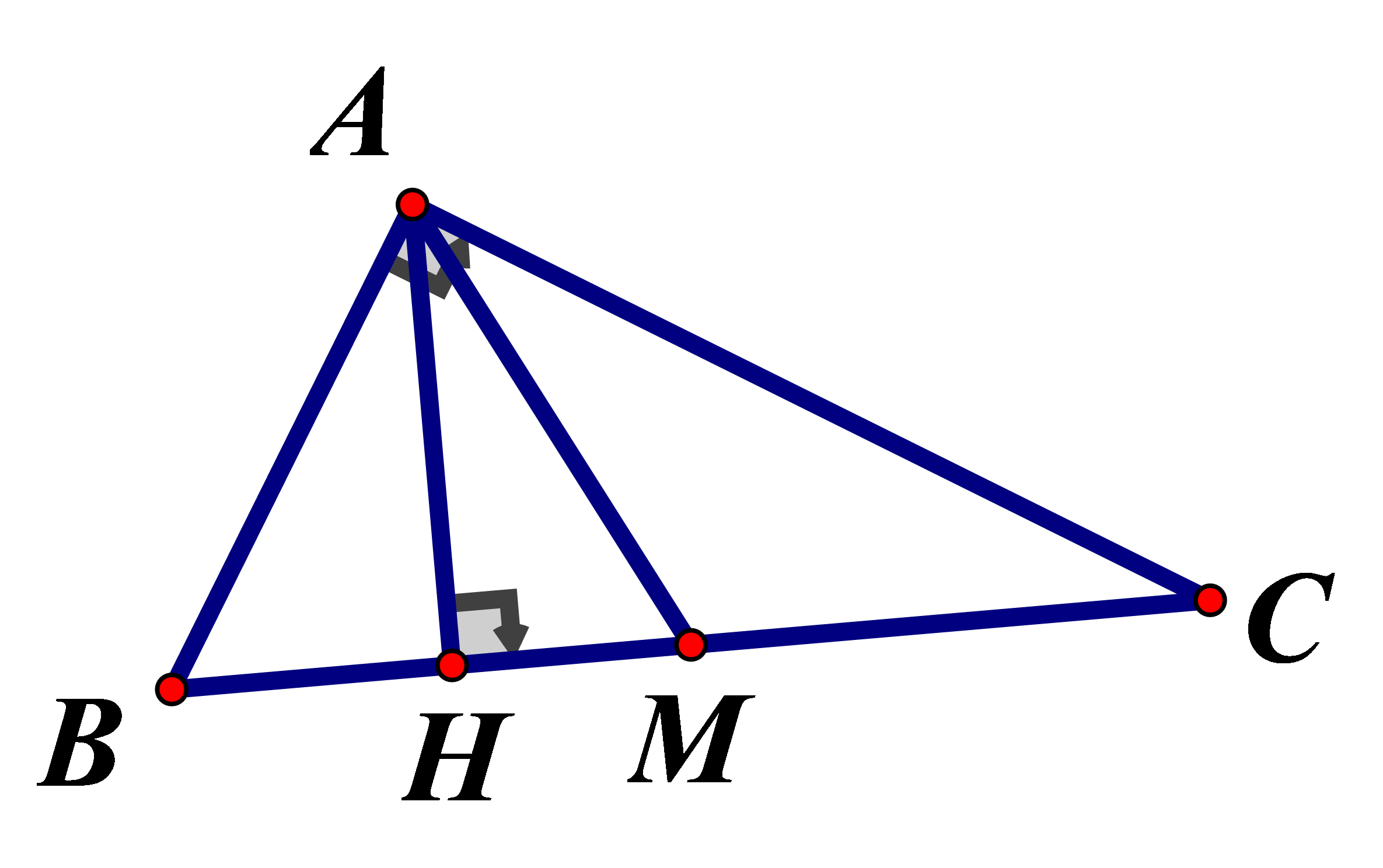
Áp dụng hệ thức lượng vào tam giác ABC vuông tại A, đường cao AH

$\frac{1}{A H^{2}} = \frac{1}{A B^{2}} + \frac{1}{A C^{2}}$ hay $\frac{1}{A H^{2}} = \frac{1}{3^{2}} + \frac{1}{4^{2}} \Rightarrow A H = \sqrt{\frac{144}{25}} = 2, 4 (c m)$

Vì AM là đường trung tuyến ứng với cạnh

$B C \Rightarrow A M = \frac{B C}{2} = \frac{\sqrt{A B^{2} + A C^{2}}}{2} = \frac{\sqrt{3^{2} + 4^{2}}}{2} = 2, 5 (c m)$

$\Rightarrow H M = \sqrt{A M^{2} - A H^{2}}$ (định lý Pytago) $= \sqrt{2, 5^{2} - 2, 4^{2}} = \frac{7}{10} c m$

Chọn đáp án B

Câu 34:

Kết quả rút gọn biểu thức $A = \frac{3 x + \sqrt{9 x} - 3}{x + \sqrt{x} - 2} - \frac{\sqrt{x} + 1}{\sqrt{x} + 2} - \frac{\sqrt{x} - 2}{\sqrt{x} - 1} (\begin{array}{l} x \geq 0 \\ x \neq 1 \end{array})$

$A . \frac{\sqrt{x} + 1}{\sqrt{x} + 2}$

$B . - \frac{\sqrt{x} + 1}{\sqrt{x} - 1}$

$C . \frac{\sqrt{x} + 1}{\sqrt{x} - 1}$

$D . \frac{\sqrt{x} - 1}{\sqrt{x} + 1}$

Xem đáp án

$\begin{array}{l} A = \frac{3 x + \sqrt{9 x} - 3}{x + \sqrt{x} - 2} - \frac{\sqrt{x} + 1}{\sqrt{x} + 2} - \frac{\sqrt{x} - 2}{\sqrt{x} - 1} (\begin{array}{l} x \geq 0 \\ x \neq 1 \end{array}) \\ = \frac{3 x + 3 \sqrt{x} - 3 - (\sqrt{x} + 1) (\sqrt{x} - 1) + (\sqrt{x} - 2) (\sqrt{x} + 2)}{(\sqrt{x} + 2) (\sqrt{x} - 1)} \\ = \frac{3 x + 3 \sqrt{x} - 3 - x + 1 - x + 4}{(\sqrt{x} + 2) (\sqrt{x} - 1)} = \frac{x + 3 \sqrt{x} + 2}{(\sqrt{x} + 2) (\sqrt{x} - 1)} = \frac{(\sqrt{x} + 1) (\sqrt{x} + 2)}{(\sqrt{x} + 2) (\sqrt{x} - 1)} = \frac{\sqrt{x} + 1}{\sqrt{x} - 1} \end{array}$

Chọn đáp án C

Câu 35:

Cho tam giác ABC cân tại $A, ∠ A = 120^{0}, B C = 2 c m, B H ⊥ A C (H \in A C) .$ Độ dài HC nhận giá trị nào sau đây ?

$A . H C = \frac{2 + \sqrt{3}}{2} c m$

$B . H C = \frac{\sqrt{3} + 1}{2} c m$

$C . H C = \sqrt{3} c m$

$D . H C = 0, 5 c m$

Xem đáp án

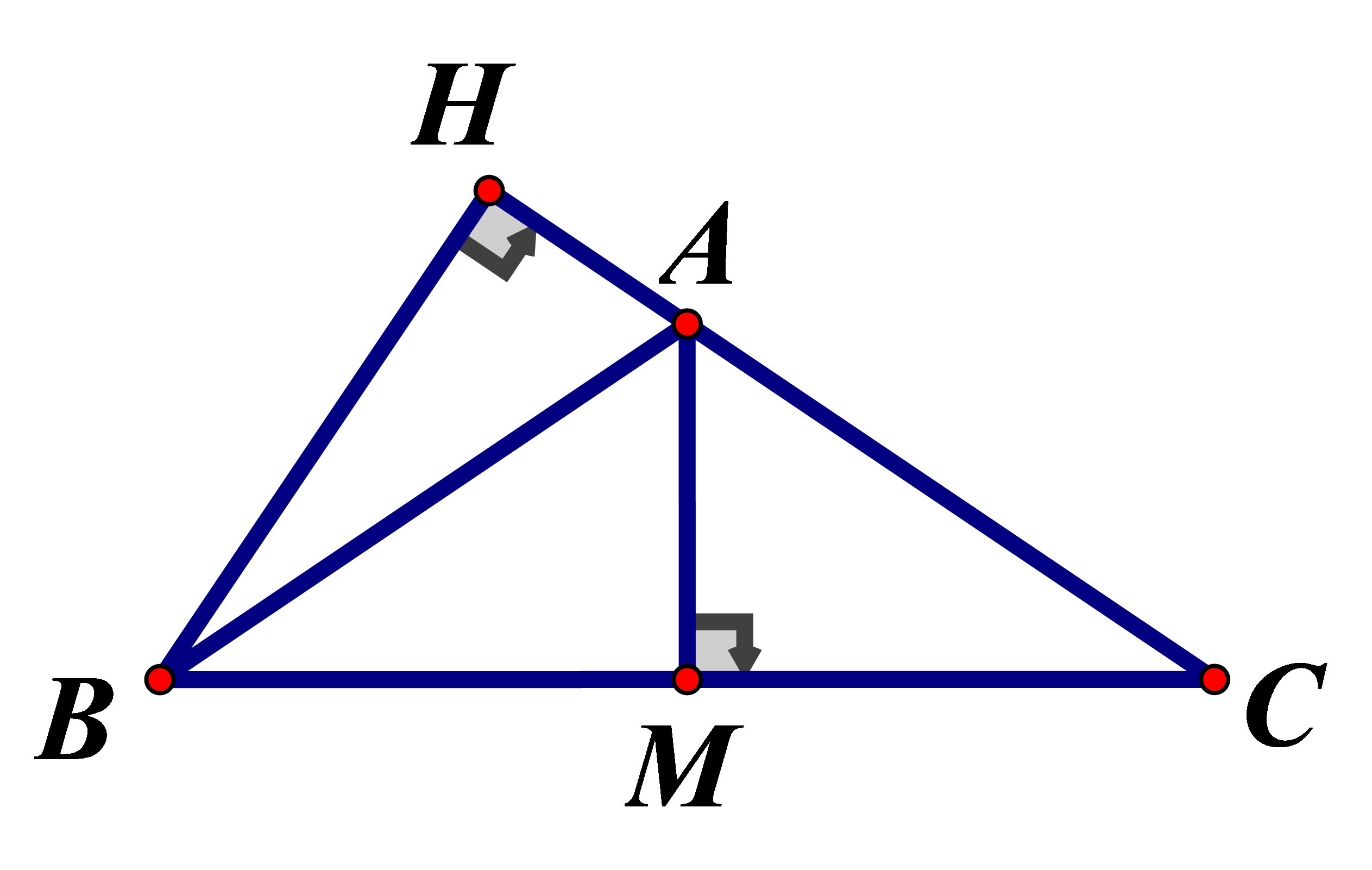
Vẽ $A M ⊥ B C \Rightarrow A M$ cũng là đường trung tuyến, là phân giác

$\Rightarrow \{\begin{cases} M C = 1 c m \\ ∠ M A C = 60^{0} \end{cases}$ $\Rightarrow A C = \frac{M C}{\sin 60^{0}} = \frac{2 \sqrt{3}}{3}$

$∠ H A B = 180^{0} - 120^{0} = 60^{0} \Rightarrow \cos ∠ H A B = \frac{A H}{A B}$

$\begin{array}{l} \Rightarrow A H = A B . \cos 60^{0} = A C . \frac{1}{2} = \frac{2 \sqrt{3}}{3} . \frac{1}{2} = \frac{\sqrt{3}}{3} \\ \Rightarrow H C = H A + A C = \frac{\sqrt{3}}{3} + \frac{2 \sqrt{3}}{3} = \sqrt{3} (c m) \end{array}$

Chọn đáp án C

Câu 36:

Biết đồ thị hàm số $y = a x + 5$ đi qua điểm $A (2; - 3)$ . Hệ số a là :

$A . a = - 1$

$B . a = 1$

$C . a = 3$

$D . a = - 4$

Xem đáp án

$y = a x + 5$ qua $A (2; - 3) \Rightarrow \{\begin{cases} x = 2 \\ y = - 3 \end{cases}$ $\Rightarrow - 3 = 2 a + 5 \Leftrightarrow a = - 4$

Chọn đáp án D

Câu 37:

Trong các câu sau, câu nào sai ?

$A . \frac{x^{2} - y^{2}}{{(x - 1)}^{2}} = \frac{y^{2} - x^{2}}{- {(1 - x)}^{2}}$

$B . \frac{x^{2} y^{3}}{x y^{4}} = \frac{x}{y}$

$C . \frac{{(x - y)}^{3}}{{(2 x - y)}^{2}} = \frac{{(y - x)}^{3}}{{(y - 2 x)}^{2}}$

$D . \frac{x (x - 1)}{x - 1} = x$

Xem đáp án

Áp dụng tính chất rút gọn phân thức, câu rút gọn sai là C, do

${(x - y)}^{3} \neq {(y - x)}^{3}$

Vậy chọn đáp án C

Câu 38:

Cho phương trình x+y=1 (1) .Phương trình nào dưới đây có thể kết hợp với (1) để được một hệ phương trình bậc nhất hai ẩn có vô số nghiệm?

$A .3 x - 2 y = 5$

$B . x + 3 y = 9$

$C .3 x + y = 1$

$D .2 x + 2 y = 2$

Xem đáp án

Ta có: $\{\begin{cases} x + y = 1 \\ 2 x + 2 y = 2 \end{cases}$ có $\frac{a}{a'} = \frac{b}{b'} = \frac{c}{c'}$ nên hệ vô số nghiệm

Chọn đáp án D

Câu 39:

Chọn khẳng định đúng ?

Tâm của đường tròn đi qua ba điểm A,B,C phân biệt không thẳng hàng là giao điểm của :

$A . B a đ ư ờ n g t r u n g t r ự c ứ n g v ớ i b a c ạ n h c ủ a t a m g i á c A B C$

$B . B a đ ư ờ n g t r u n g t u y ế n ứ n g v ớ i b a c ạ n h c ủ a t a m g i á c A B C$

$C . B a đ ư ờ n g p h â n g i á c ứ n g v ớ i b a c ạ n h c ủ a t a m g i á c A B C$

$D . B a đ ư ờ n g c a o ứ n g v ớ i b a c ạ n h c ủ a t a m g i á c A B C$

Xem đáp án

Chọn đáp án A, giao điểm ba đường trung trực.

Câu 40:

Hiệu số diện tích của hai tam giác đồng dạng là $18 m^{2}$ và tỉ số diện tích lớn và diện tích nhỏ là bình phương của một số tự nhiên. Diện tích tam giác nhỏ $(m^{2})$ là một số tự nhiên và có một cạnh bằng 3m.Cạnh tương ứng với cạnh này trong tam giác là :

$A .9 m$

$B .6 m$

$C .6 \sqrt{2} m$

$D .12 m$

Xem đáp án

Gọi K là tỉ số đồng dạng

$\Rightarrow k^{2} = \frac{x}{x + 18} \Rightarrow k^{2} x + 18 k^{2} = x$ $\Leftrightarrow x (k^{2} - 1) = 18 k^{2}$

$\Rightarrow x = \frac{18 k^{2}}{k^{2} - 1} \Rightarrow \frac{18}{x} = \frac{k^{2} - 1}{k^{2}}$ $\Rightarrow k^{2} - 1 \in U (18) \Rightarrow k^{2} - 1 = 3 (t m) \Leftrightarrow k = 2 (d o k \in N *)$

Nên tỉ số đồng dang là 2 , cạnh tương ứng với cạnh là . Chọn B

Câu 41:

Biều thức $\sqrt{\frac{2 x - 1}{x^{2} + 1}}$ xác định khi :

$A . x \neq 0$

$B . x \geq \frac{1}{2}$

$C . x \geq - \frac{1}{2}$

$D . x > 0$

Xem đáp án

$\sqrt{\frac{2 x - 1}{x^{2} + 1}}$ xác định khi $2 x - 1 \geq 0 \Leftrightarrow x \geq \frac{1}{2}$ . Chọn đáp án B

Câu 42:

Cho đường tròn (O) đường kính AC và điểm B trên đường tròn sao cho số đo

\overset{⏜}{B C} = 60^{0} .

Qua B kẻ dây BD vuông góc với AC qua D kẻ

D F / / A C (F

thuộc đường

(O))

.Tính số đo

\overset{⏜}{D F}

$A . s d \overset{⏜}{D F} = 45^{0}$

$B . s d \overset{⏜}{D F} = 120^{0}$

$C . s d \overset{⏜}{D F} = 60^{0}$

$D . s d \overset{⏜}{D F} = 90^{0}$

Xem đáp án

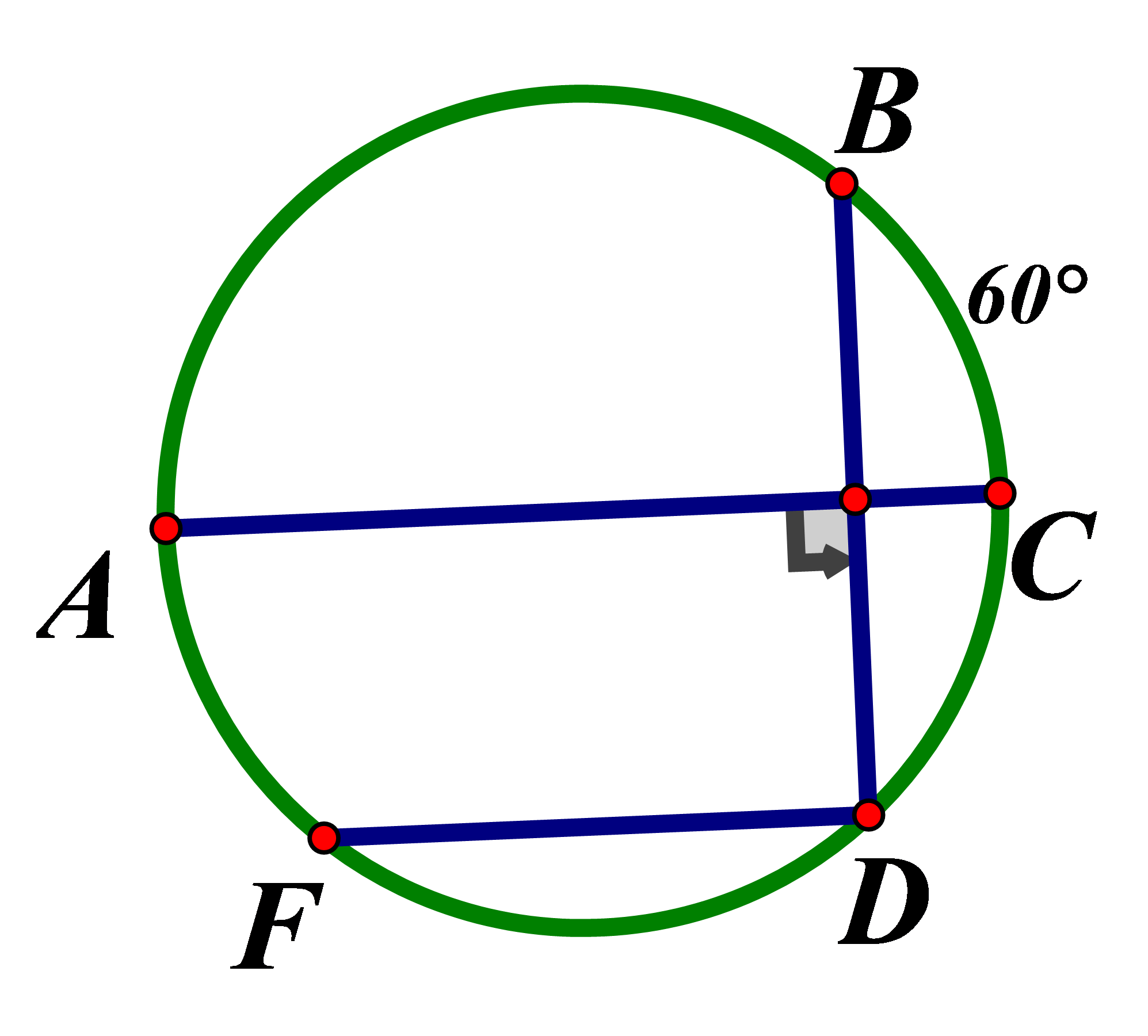
Vì $B D ⊥ A C \Rightarrow s d \overset{⏜}{C D} = s d \overset{⏜}{B C} = 60^{0}$

Vì $A C / / F D \Rightarrow s d \overset{⏜}{C D} = s d \overset{⏜}{A F} = 60^{0}$

$\Rightarrow s d \overset{⏜}{F D} = 180^{0} - (s d \overset{⏜}{A F} + s d \overset{⏜}{C D}) = 180^{0} - 120^{0} = 60^{0}$

Chọn C.

Câu 43:

Cho hệ phương trình $\{\begin{cases} m x - y = m + 2 \\ x + y = 1 \end{cases} .$ Giá trị m để hệ có nghiệm duy nhất là :

$A . m \neq - 1$

$B . m = 1$

$C . m \neq - 2$

$D . m \neq 3$

Xem đáp án

$\{\begin{cases} m x - y = m + 2 \\ x + y = 1 \end{cases}$

Để hệ có nghiệm duy nhất $\Leftrightarrow \frac{m}{1} \neq \frac{- 1}{1} \Leftrightarrow m \neq - 1$ . Chọn đáp án A

Câu 44:

Đường thẳng $y = (3 - m) x - 2$ tạo với trục Ox một góc tù khi :

$A . m = - 2$

$B . m < 3$

$C . m > 3$

$D . m = 3$

Xem đáp án

Để $y = (3 - m) x - 2$ tạo với Ox góc tù thì $3 - m < 0 \Leftrightarrow m > 3$

Chọn đáp án C

Câu 45:

Kết quả phép tính $\sqrt{2} . \sqrt{32}$ là :

$A . \sqrt{34}$

$C .64$

$D .8$

Xem đáp án

$\sqrt{2} . \sqrt{32} = \sqrt{64} = 8$

Chọn đáp án D

Câu 46:

Có bao nhiêu cặp $(m, n)$ các số nguyên thỏa mãn phương trình $m + n = m n$

$A .1$

$B .3$

$C .2$

$D .4$

Xem đáp án

$\begin{array}{l} m + n = m n \Leftrightarrow m - m n + n - 1 = - 1 \Leftrightarrow m (1 - n) - (1 - n) = - 1 \\ \Leftrightarrow (1 - n) (m - 1) = - 1 = (- 1) .1 = 1. (- 1) \\ \Leftrightarrow [\begin{array}{l} \{\begin{cases} 1 - n = - 1 \\ m - 1 = 1 \end{cases} \\ \{\begin{cases} 1 - n = 1 \\ m - 1 = - 1 \end{cases} \end{array} \Leftrightarrow [\begin{array}{l} \{\begin{cases} n = 2 \\ m = 2 \end{cases} \\ \{\begin{cases} n = 0 \\ m = 0 \end{cases} \end{array} \end{array}$

Có 2 cặp nghiệm. Chọn đáp án C.

Câu 47:

Cho phương trình $(m - 1) x + (m + 1) y = 1.$ Giá trị của m để cặp số (1;1) là nghiệm của phương trình là :

$A . m = - \frac{1}{2}$

$B . m = \frac{5}{2}$

$C . m = \frac{1}{2}$

$D . m = \frac{3}{2}$

Xem đáp án

Để $(1; 1)$ là nghiệm thì $\{\begin{cases} x = 1 \\ y = 1 \end{cases}$

$\Rightarrow (m - 1) .1 + (m + 1) .1 = 1 \Leftrightarrow m - 1 + m + 1 = 1 \Leftrightarrow m = \frac{1}{2}$

Chọn đáp án C

Câu 48:

Tìm giá trị m để hai đường thẳng $y = (m^{2} - 1) x + m + 2$ và $y = (5 - m) x + 2 m + 5$ song song với nhau

$A . m = - 3$

$B . m = 3$

$C . m = 1$

$D . m = 2$

Xem đáp án

Để đường thẳng $y = (m^{2} - 1) x + m + 2$ và $y = (5 - m) x + 2 m + 5$ đường thẳng song song thì

$\{\begin{cases} m^{2} - 1 = 5 - m \\ m + 2 \neq 2 m + 5 \end{cases} \Leftrightarrow \{\begin{cases} m^{2} + m - 6 = 0 \\ m \neq - 3 \end{cases} \Leftrightarrow \{\begin{cases} [\begin{array}{l} m = 2 \\ m = - 3 \end{array} \\ m \neq - 3 \end{cases} \Rightarrow m = 2$

Chọn đáp án D

Câu 49:

Tính giá trị của biểu thức $A = \frac{3}{2^{2}} . \frac{8}{3^{2}} . \frac{15}{4^{2}} ...... \frac{899}{30^{2}}$ ta được kết quả là :

$A . \frac{13}{45}$

$B . \frac{31}{20}$

$C . \frac{1}{2}$

$D . \frac{31}{60}$

Xem đáp án

$\begin{array}{l} A = \frac{3}{2^{2}} . \frac{8}{3^{2}} . \frac{15}{4^{2}} ...... \frac{899}{30^{2}} = \frac{1.3.2.4.3.5......29.31}{2.2.3.3.4.4......30.30} \\ = \frac{1.2.3....29}{2.3.4.....30} . \frac{3.4.5.......31}{2.3.4......30} = \frac{1}{30} . \frac{31}{2} = \frac{31}{60} \end{array}$

Chọn đáp án D

Câu 50:

Điều kiện để $\sqrt{5 - 3 x}$ có nghĩa là :

$A . x \leq \frac{3}{5}$

$B . x \leq \frac{5}{3}$

$C . x > \frac{5}{3}$

$D . x \geq \frac{3}{5}$

Xem đáp án

$\sqrt{5 - 3 x}$ có nghĩa thì $5 - 3 x \geq 0 \Leftrightarrow x \leq \frac{3}{5} .$ Chọn đáp án B