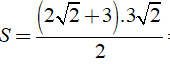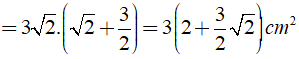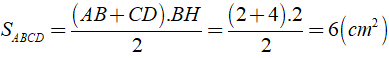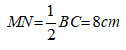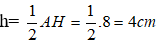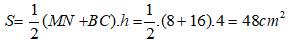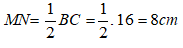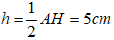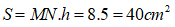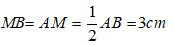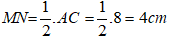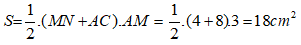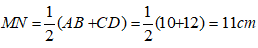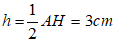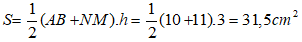Bài tập Diện tích hình thang (có lời giải chi tiết)
-
1286 lượt thi
-
19 câu hỏi
-
20 phút
Danh sách câu hỏi
Câu 1:
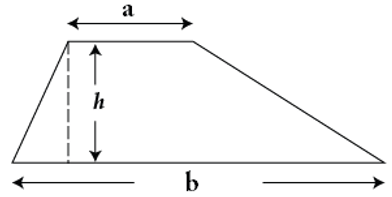
Hình thang có độ dài đáy lần lượt là 2√2 cm, 3cm và chiều cao là 3√2 cm. Diện tích của hình thang là ?
 Xem đáp án
Xem đáp án
Ta có: S = 1/2( a + b ).h
Khi đó ta có:
Chọn đáp án B.
Câu 2:
Hình thang có độ dài đáy lần lượt là 6cm, 4cm và diện tích hình thang đó là . Chiều cao hình thang có độ dài là
 Xem đáp án
Xem đáp án
Diện tích của hình thang là S = 1/2( a + b ).h
⇒ ( a + b ).h = 2S ⇔ h = (2S)/(a + b).
Khi đó, chiều cao của hình thang là h = (2.15)/(6 + 4) = 3( cm ).
Chọn đáp án A.
Câu 3:
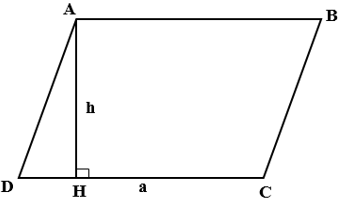
Cho hình bình hành ABCD ( AB//CD ) có AB = CD = 4cm, độ dài đường cao hình bình hành là h = 2cm. Diện tích của hình bình hành là?
 Xem đáp án
Xem đáp án
Ta có : S = a.h
Khi đó ta có: S = 4.2 = 8 .
Chọn đáp án B.
Câu 4:
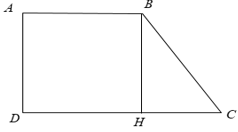
Cho hình thang vuông ABCD , trong đó có , AB = 2cm, CD = 4cm. Diện tích của hình thang vuông ABCD là
 Xem đáp án
Xem đáp án
Xét hình thang ABCD
Từ B kẻ BH ⊥ CD, khi đó ta được hình chữ nhật ABHD ⇒ AB = DH = 2cm
⇒ HC = CD - DH = 4 - 2 = 2cm.
+ Xét Δ BDC có BH là đường cao đồng thời là đường trung tuyến
⇒ Δ BDC là tam giác cân tại B.
Chọn đáp án D.
Câu 5:
Cho tam giác ABC có BC = 16cm ,đường cao AH = 8cm. Gọi M và N lần lượt là trung điểm của AB và AC. Tính diện tích của tứ giác MNCB?
 Xem đáp án
Xem đáp án
Xét tam giác ABC có M và N lần lượt là trung điểm của AB và AC nên MN là đường trung bình của tam giác ABC.
Suy ra: MN // BC và
Do đó, tứ giác MNCB là hình thang .
Vì AH = 8cm nên đường cao kẻ từ M đến BC bằng
Diện tích hình thang MNCB là :
Chọn đáp án A
Câu 6:
Cho tam giác ABC có M, N và P lần lượt là trung điểm của AB, AC và P. Biết đường cao AH = 10cm và BC = 16cm . Tính diện tích tứ giác MNPB?
 Xem đáp án
Xem đáp án
Xét tam giác ABC có M và N lần lượt là trung điểm của AB và AC nên MN là đường trung bình của tam giác ABC
Suy ra: MN// BC và
Tương tự, có NP là đường trung bình của tam giác nên: NP // AB
Xét tứ giác MNPB có MN// BC và NP // AB
Suy ra: tứ giác MNPB là bình hành.
Tam giác ABC có đường cao AH = 10cm nên đường cao ứng với cạnh đáy của hình bình hành MNPB là:
Diện tích hình bình hành MNPB là:
Chọn đáp án C
Câu 7:
Cho tam giác ABC vuông tại A có AB = 6cm và BC = 10cm . Gọi M và N theo thứ tự là trung điểm của AB và BC. Tính diện tích của tứ giác MNCA?
 Xem đáp án
Xem đáp án
Vì M là trung điểm của AB nên:
Áp dụng định lí py tago vào tam giác ABC có:
Suy ra: AC = 8cm
Xét tam giác ABC có M và N lần lượt là trung điểm của AB và BC nên MN là đường trung bình của tam giác ABC nên: MN// AC và
Suy ra: tứ giác MNCA là hình thang vuông.
Diện tích hình thang MNCA là:
Chọn đáp án D
Câu 9:
Cho hình thang ABCD (AB// CD) có AB = 6cm và CD = 10cm. Biết diện tích hình thang ABCD là 60cm2. Tính diện tích tam giác ACD?
 Xem đáp án
Xem đáp án
Chọn A
Câu 10:
Cho hình thang ABCD có AB// CD; AB = 10cm , CD = 12cm, đường cao AH = 6cm . Gọi M và N lần lượt là trung điểm của AD và BC. Tính diện tích tứ giác ABNM?
 Xem đáp án
Xem đáp án
Xét hình thang ABCD có M và N lần lượt là trung điểm của AD và BC nên MN là đường trung bình của hình thang:
Suy ra: MN// AB// CD và
Suy ra: tứ giác MNCD là hình thang.
Vì M là trung điểm của AD và đường cao AH = 6cm nên chiều cao xuất phát từA của hình thang MNCD là:
Diện tích hình thang ABNM là :
Chọn đáp án D
Câu 11:
Một hình thang có đáy nhỏ là 11 cm, chiều cao là 5 cm, diện tích là . Độ dà đáy lớn là:
 Xem đáp án
Xem đáp án
Gọi đáy lớn của hình thang là a (cm; a > 0).
Diện tích hình thang
S = ó= 65.
ó55 + 5a = 130 ó 5a = 75 ó a = 15 ™
Vậy độ dài đáy lớn là 15 cm.
Đáp án cần chọn là: D
Câu 12:
Tính diện tích mảnh đất hình thang vuông ABCD có độ dài hai đáy AB = 10 cm; DC = 13 cm; (hình vẽ), biết tam giác BEC vuông tại E và có diện tích bằng .
 Xem đáp án
Xem đáp án
Tứ giác ABED có nên là hình chữ nhật. Suy ra DE = AB = 10 cm. Do đó: EC = DC – DE = 13 – 10 = 3 (cm)
Ta có:
SBEC = BE. EC => BE = = = 9 (cm)
SABED = AB.BE = 10.9 = 90 (cm2)
SABCD = SABED + SBEC = 90 + 13, 5 = 103, 5 (cm2).
Đáp án cần chọn là: A
Câu 13:
Tính diện tích mảnh đất hình thang vuông ABCD có độ dài hai đáy AB = 9 cm; DC = 13, 5 cm; (hình vẽ), biết tam giác BEC vuông tại E và có diện tích bằng .
 Xem đáp án
Xem đáp án
Tứ giác ABED có = 900 nên là hình chữ nhật. Suy ra DE = AB = 9 cm.
Do đó: EC = DC – DE = 13, 5 – 9 = 4, 5 (cm)
Ta có:
SBEC = BE. EC => BE === 8 (cm)
SABED = AB.BE = 9.8 = 72 (cm2)
SABCD = SABED + SBEC = 72 + 18 = 90 (cm2).
Đáp án cần chọn là: C
Câu 14:
Cho hình vuông ABCD có cạnh 10m. Hãy xác định điểm E trên cạnh AB sao cho diện tích hình thang vuông BCDE bằng diện tích vuông ABCD
 Xem đáp án
Xem đáp án
Gọi BE = x (m).
Diện tích hình vuông ABCD là: SABCD = AB2 = 102 = 100 (m2)
Diện tích hình thang vuông BCDE là:
SBCDE = = = 5 (x+10)
Vì diện tích hình thang vuông BCDE bằng diện tích hình vuông ABCD nên ta có:
SBCDE = SABCD = 5(x + 10) =.100 óx + 10 = 16 ó x = 6 (m)
Vậy điểm E ở trên cạnh AB sao cho BE = 6 m.
Đáp án cần chọn là: B
Câu 15:
Cho hình vuông ABCD có cạnh 20 m. Hãy xác định điểm E trên cạnh AB sao cho diện tích hình thang vuông BCDE bằng diện tích vuông ABCD
 Xem đáp án
Xem đáp án
Gọi BE = x (m).
Diện tích hình vuông ABCD là: SABCD = AB2 = 202 = 400 (m2)
Diện tích hình thang vuông BCDE là:
SBCDE = = = 10(x + 20)
Vì diện tích hình thang vuông BCDE bằng diện tích hình vuông ABCD nên ta có:
SBCDE = SABCD = 10(x + 20) = .400 óx + 20 = 30 ó x = 10 (m)
Vậy điểm E ở trên cạnh AB sao cho BE = 10 m hay E là trung điểm đoạn AB.
Đáp án cần chọn là: D
Câu 16:
Cho hình bình thang ABCD (AB//CD), đường cao AH, AB = 4 cm; CD = 8 cm, diện tích hình thang là thì AH bằng
 Xem đáp án
Xem đáp án
SABCD =
=> AH = = = 9 (cm)
Đáp án cần chọn là: D
Câu 17:
Cho hình bình thang ABCD (AB//CD), đường cao AH, AB = 5 cm; CD = 10 cm, diện tích hình thang là thì AH bằng
 Xem đáp án
Xem đáp án
SABCD =
=> AH = = = 8 (cm)
Đáp án cần chọn là: A
Câu 18:
Một hình thang có đáy nhỏ là 9 cm, chiều cao là 4 cm, diện tích là . Đáy lớn là:
 Xem đáp án
Xem đáp án
Tổng hai đáy của hình thang là: 2.50:4 = 25 cm.
Độ dài đáy lớn là: 25 – 9 = 16 cm.
Đáp án cần chọn là: C
Câu 19:
Chọn câu sai:
 Xem đáp án
Xem đáp án
Diện tích hình thang bằng nửa tích của tổng hai đáy với chiều cao: S =
Diện tích hình bình hành bằng tích một cạnh với chiều cao ứng với cạnh đó: S = a. h
Diện tích hình thoi bằng nửa tích hai đường chéo: S = d1. d2
Đáp án cần chọn là: C