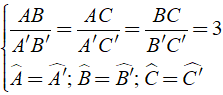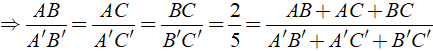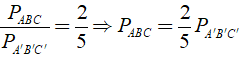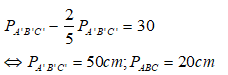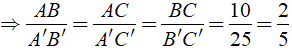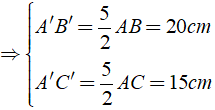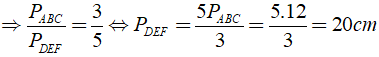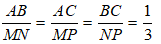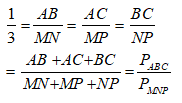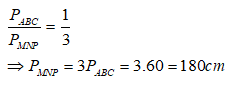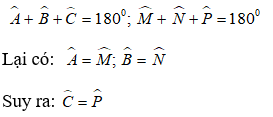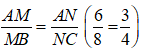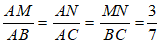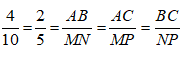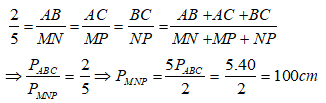16 câu hỏi trắc nghiệm thuộc Bài tập Khái niệm hai tam giác đồng dạng (có lời giải chi tiết)

Câu 1:

Nếu Δ MNP đồng dạng ΔABC thì

A. MN/AB = MP/AC

B. MN/AB = MP/BC

C. MN/AB = NP/AC

D. MN/BC = NP/AC

Xem đáp án

Ta có: Δ MNP đồng dạng Δ ABC ⇒ MN/AB = NP/BC = MP/AC

Chọn đáp án A.

Câu 2:

Cho Δ ABC đồng dạng Δ A'B'C' có AB = 3A'B'. Kết quả nào sau đây sai?

A. $\hat{A} = \hat{A'}; \hat{B} = \hat{B'}$

B. $A' C' = \frac{1}{3} A C$

C. $\frac{A C}{B C} = \frac{A' C'}{B' C'} = 3$

D. $\frac{A B}{A' B'} = \frac{A C}{A' C'} = \frac{B C}{B' C'}$

Xem đáp án

Ta có: Δ ABC đồng dạng Δ A'B'C' ⇒

Đáp án C sai.

Chọn đáp án C.

Câu 3:

Cho Δ ABC đồng dạng Δ A'B'C' có AB/A'B' = 2/5. Biết hiệu số chu vi của Δ A'B'C' và Δ ABC là 30cm. Phát biểu nào sau đây đúng?

A. Chu vi của Δ ABC là 20cm, chu vi của Δ A'B'C' là 50cm.

B. Chu vi của Δ ABC là 50cm, chu vi của Δ A'B'C' là 20cm.

C. Chu vi của Δ ABC là 45cm, chu vi của Δ A'B'C' là 75cm.

D. Cả 3 đáp án đều sai.

Xem đáp án

Ta có: Δ ABC đồng dạng Δ A'B'C'

Khi đó

Mà PA'B'C' - PABC = 30cm.

Suy ra

Vậy chu vi của Δ ABC là 20cm, chu vi của Δ A'B'C' là 50cm.

Chọn đáp án A.

Câu 4:

Cho Δ ABC có AB = 8cm,AC = 6cm,BC = 10cm. Tam giác A'B'C' đồng dạng với tam giác ABC có độ dài cạnh lớn nhất là 25 cm. Tính độ dài các cạnh còn lại của Δ A'B'C' ?

A. 4cm; 3cm

B. 7,5cm; 10cm

C. 4,5cm; 6cm

D. 15cm; 20cm

Xem đáp án

Ta có: Δ ABC đồng dạng Δ A'B'C'

Chọn đáp án D.

Câu 5:

Cho Δ ABC đồng dạng Δ DEF có tỉ số đồng dạng là k = 3/5, chu vi của Δ ABC bằng 12cm. Chu vi của Δ DEF là?

A. 7,2cm

B. 20cm

C. 3cm

D. 17/3cm

Xem đáp án

Ta có: Δ ABC đồng dạng Δ DEF

Chọn đáp án B.

Câu 6:

Cho hai tam giác ABC và MNP đồng dạng với nhau. Biết $\frac{A B}{M N} = \frac{1}{3}$ và chu vi tam giác ABC là 60cm . Tính chu vi tam giác MNP?

A. 180cm

B. 20cm

C. 30cm

D. 57cm

Xem đáp án

Do tam giác ABC đồng dạng với tam giác MNP nên:

Theo tính chất của dãy tỉ số bằng nhau ta có:

Vậy

Chọn đáp án A

Câu 7:

Cho hai tam giác ABC và MNP có:

$\frac{A B}{M N} = \frac{A C}{M P} = \frac{B C}{N P} v à \hat{A} = \hat{M}; \hat{B} = \hat{N}$

Tìm khẳng định đúng

A. Hai tam giác ABC và MNP đồng dạng với nhau.

B. Chưa thể kết luận hai tam giác này đồng dạng.

C. $∠ C \neq ∠ P$

D. Tất cả sai.

Xem đáp án

Tổng ba góc trong 1 tam giác bằng 180o nên :

Do đó, hai tam giác ABC và MNP đồng dạng với nhau

Chọn đáp án A

Câu 8:

Cho tam giác ABC, gọi M, N và P theo thứ tự là trung điểm của AB, AC và BC. Khi đó tam giác AMN đồng dạng với tam giác nào

A. ΔAMC

B. ΔABC

C. ΔABP

D. ΔAPC

Xem đáp án

Xét tam giác ABC có M và N lần lượt là trung điểm của AB và AC nên MN là đường trung bình của tam giác ABC

Suy ra: MN // B C

Do đó, tam giác AMN đồng dạng với tam giác ABC ( định lí)

Chọn đáp án B

Câu 9:

Cho tam giác ABC, trên đoạn thẳng AB và AC lấy các điểm M và N sao cho AM = 6cm; MB = 8cm; AN = 3cm và AC = 7cm. Tìm khẳng định sai ?

A. MN/BC = 3/7

B. Hai tam giác AMN và ABC đồng dạng với nhau

C. MN// BC

D. Tam giác AMC đồng dạng với tam giác ABN.

Xem đáp án

Ta có: NC = AC – AN = 7 – 3 = 4cm

Vì

nên MN // BC (định lí Ta let đảo)

Suy ra: Tam giác AMN đồng dạng với tam giác ABC.

Ta có:

Chọn đáp án D

Câu 10:

Cho 2 tam giác ABC và MNP đồng dạng với nhau. Biết chu vi tam giác ABC là 40cm; AB = 4cm; MN = 10cm . Tính chu vi tam giác MNP?

A. 50cm

B. 60cm

C. 100cm

D. 80cm

Xem đáp án

Vì tam giác ABC đồng dạng với tam giác MNP nên;

Theo tính chất dãy tỉ số bằng nhau ta có:

Chọn đáp án C

Câu 11:

Cho tứ giác ABCD có đường chéo BD chia tứ giác đó thành hai tam giác đồng dạng ΔABD ⁓ ΔBDC. Cho AB = 2cm, AD = 3cm, CD = 8cm. Tính độ dài cạnh còn lại của tứ giác ABCD.

A. BC = 6cm

B. BC = 4cm

C. BC = 5cm

D. BC = 3cm

Xem đáp án

Vì ΔABD ⁓ ΔBDC nên $\frac{A B}{B D} = \frac{B D}{D C} = \frac{A D}{B C}$ , tức là $\frac{2}{B D} = \frac{B D}{8} = \frac{3}{B C}$

Ta có $B D^{2}$ = 2.8 = 16 nên BD = 4 cm

Suy ra BC = $\frac{8.3}{4}$ = 6 cm

Vậy BD = 4cm, BC = 6cm

Đáp án: A

Câu 12:

Hình thang ABCD (AB // CD) có AB = 10cm, CD = 25cm, hai đường chéo cắt nhau tại O. Chọn khẳng định đúng.

A. ΔAOB ⁓ ΔCOD với tỉ số đồng dạng k = 2

B. $\frac{A O}{O C} = \frac{2}{3}$

C. ΔAOB ⁓ ΔCOD với tỉ số đồng dạng $k = \frac{2}{5}$

D. ΔAOB ⁓ ΔCOD với tỉ số đồng dạng $k = \frac{5}{2}$

Xem đáp án

AB // CD nên ΔAOB ⁓ ΔCOD.

Tỉ số đồng dạng

$\frac{A O}{O C} = \frac{B O}{O D} = \frac{A B}{C D} = \frac{10}{25} = \frac{2}{5}$

Đáp án: C

Câu 13:

Hình thang ABCD (AB // CD) có AB = 9cm, CD = 12cm, hai đường chéo cắt nhau tại O. Chọn khẳng định không đúng.

A. ΔAOB ⁓ ΔDOC với tỉ số đồng dạng $k = \frac{3}{4}$

B. $\frac{A O}{O C} = \frac{B O}{O D} = \frac{3}{4}$

C. ΔAOB ⁓ ΔCOD với tỉ số đồng dạng $k = \frac{3}{4}$

D. $\hat{A B D} = \hat{B D C}$

Xem đáp án

AB // CD nên ΔAOB ⁓ ΔCOD.

Tỉ số đồng dạng $\frac{A O}{O C} = \frac{B O}{O D} = \frac{A B}{C D} = \frac{9}{12} = \frac{3}{4}$ nên B, C đúng

Lại có: AB // CD nên $\hat{A B D} = \hat{B D C}$ (so le trong nên D đúng

Đáp án A sai vì viết sai thứ tự các đỉnh của hai tam giác đồng dạng

Đáp án: A

Câu 14:

Cho tam giác ABC, điểm M thuộc cạnh BC sao cho $\frac{M B}{M C} = \frac{1}{2}$ . Đường thẳng đi qua M và song song với AC cắt AB ở D. Đường thẳng đi qua M và song song với AB cắt AC ở E. Biết chu vi tam giác ABC bằng 30cm. Chu vi của các tam giác DBM và EMC lần lượt là

A. 10cm; 15cm

B. 12cm; 16cm

C. 20cm; 10cm

D. 10cm; 20cm

Xem đáp án

Ta có: MD // AC nên ΔDBM ~ ΔABC. Suy ra :

$\frac{D B}{A B} = \frac{B M}{B C} = \frac{D M}{A C} = \frac{D B + B M + D M}{A B + B C + C A}$

Do đó $\frac{1}{3} = \frac{P_{B D M}}{P_{A B C}}$

Chu vi ΔDBM bằng 30. $\frac{1}{3}$ = 10cm

Ta có ME // AB nên ΔEMC ~ ΔABC. Suy ra

$\frac{E M}{A B} = \frac{M C}{B C} = \frac{E C}{A C} = \frac{E M + M C + E C}{A B + B C + A C}$

do đó $\frac{2}{3} = \frac{P_{E M C}}{P_{A B C}}$

Chu vi ΔEMC bằng 30. $\frac{2}{3}$ = 20 cm

Vậy chu vi ΔDBM và chu vi ΔEMC lần lượt là 10cm; 20cm

Đáp án: D

Câu 15:

Cho tam giác ABC, điểm M thuộc cạnh BC sao cho $\frac{M B}{M C} = \frac{1}{2}$ . Đường thẳng đi qua M và song song với AC cắt AB ở D. Đường thẳng đi qua M và song song với AB cắt AC ở E. Tỉ số chu vi hai tam giác ΔDBM và ΔEMC là

A. $\frac{1}{2}$

B. $\frac{1}{3}$

C. $\frac{2}{3}$

D. $\frac{1}{4}$

Xem đáp án

Ta có: MD // AC nên ΔDBM ~ ΔABC. Suy ra

$\frac{D B}{A B} = \frac{B M}{B C} = \frac{D M}{A C} = \frac{D B + B M + D M}{A B + B C + C A}$

Do đó $\frac{1}{3} = \frac{P_{B D M}}{P_{A B C}}$ (1)

Ta có ME // AB nên ΔEMC ~ ΔABC. Suy ra

$\frac{E M}{A B} = \frac{M C}{B C} = \frac{E C}{A C} = \frac{E M + M C + E C}{A B + B C + A C}$

do đó $\frac{2}{3} = \frac{P_{E M C}}{P_{A B C}}$ (2)

Từ (1) và (2) suy ra:

$\frac{P_{B D M}}{P_{A B C}} : \frac{P_{E M C}}{P_{A B C}} = \frac{1}{3} : \frac{2}{3} \Leftrightarrow \frac{P_{B D M}}{P_{E M C}} = \frac{1}{2}$

Đáp án: A

Câu 16:

Cho hình bình hành ABCD. Trên đường chéo AC lấy điểm E sao cho AC = 3AE. Qua E vẽ đường thẳng song song với CD, cắt AD và BC theo thứ tự ở M và N. Cho các khẳng địnha su

(I) ΔAME ~ ΔADC, tỉ số đồng dạng $k_{1} = \frac{1}{3}$

(II) ΔCBA ~ ΔADC, tỉ số đồng dạng bằng $k_{2} = 1$

(III) ΔCNE ~ ΔADC, tỉ số đồng dạng $k_{3} = \frac{2}{3}$

Chọn câu đúng.

A. (I) đúng, (II) và (III) sai

B. (I) và (II) đúng, (III) sai

C. Cả (I), (II), (III) đều đúng

D. Cả (I), (II), (III) đều sai.

Xem đáp án

Vì ABCD là hình bình hành nên ME // DE và EN // AB.

+ ME // DC nên ΔAME ~ ΔADC, tỉ số đồng dạng $\frac{A E}{A C} = \frac{1}{3}$

+ Vì ABCD là hình bình hành nên góc B = D; AD = BC; AB = DC

=> ΔCBA ~ ΔADC

ΔCBA ~ ΔADC, tỉ số đồng dạng bằng 1

+ EN // AB nên ΔCNE ~ ΔADC, do đó ΔCNE ~ ΔADC, tỉ số đồng dạng $\frac{C E}{A C} = \frac{2}{3}$

Vậy cả (I), (II), (III) đều đúng.

Đáp án: C