Dạng 1: Luyện tập đối xứng tâm có đáp án
-
367 lượt thi
-
14 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Trong các hình sau, hình nào có tâm đối xứng? Với các hình đó, hãy chỉ ra tâm đối xứng của hình.
a) Đoạn thẳng AB Xem đáp án
Xem đáp án
Câu 3:
 Xem đáp án
Xem đáp án
Câu 4:
 Xem đáp án
Xem đáp án
Câu 6:
 Xem đáp án
Xem đáp án
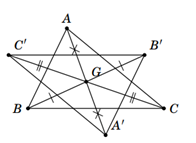
• Trên tia đối của tia GA lấy A' sao cho GA' = GA.
• Trên tia đối của tia GB lấy B' sao cho GB' = GB.
• Trên tia đối của tia GC lấy C' sao cho GC' = GC.
Nối A', B', C' với nhau, ta được tam giác đối xứng với tam giác ABC qua điểm G.
Điểm G cũng là trọng tâm của tam giác A'B'C'
Câu 7:
Cho tứ giác ABCD và một điểm O. Hãy vẽ tứ giác A'B'C'D' đối xứng với tứ giác ABCD qua O.
 Xem đáp án
Xem đáp án
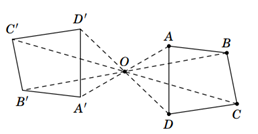
• Vẽ các điểm A', B', C', D' lần lượt đối xứng với các điểm A, B, C, D qua O.
• Nối A'B', B'C', C'D', D'A' ta được tứ giác A'B'C' đối xứng với tứ giác ABCD qua O
Câu 8:
 Xem đáp án
Xem đáp án
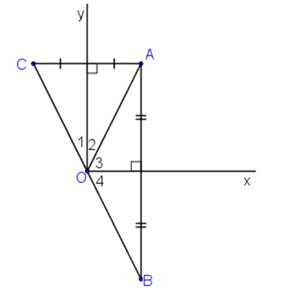
+ B đối xứng với A qua Ox
=> Ox là đường trung trực của AB
=> OA = OB (1)
+ C đối xứng với A qua Oy
=> Oy là đường trung trực của AC
=> OA = OC (2)
Từ (1) và (2) suy ra OB = OC (*).
+ Xét OAC cân tại O (do OA = OC) có Oy là đường trung trực
=> Oy đồng thời là đường phân giác
Xét OAB cân tại O có Ox là đường trung trực
=> Ox đồng thời là đường phân giác
Do đó ta có:
=> B, O, C thẳng hàng (**)
Từ (*) và (**) suy ra O là trung điểm BC
=> B đối xứng với C qua O.
Câu 9:
 Xem đáp án
Xem đáp án
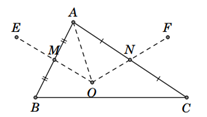
Ta có B đối xứng với A qua M, E đối xứng với O qua M nên BE đối xứng với AO qua M. Suy ra BE = AO (1).
Chứng minh tương tự, ta được CF đối xứng với AO qua N.
Suy ra CF = AO (2).
Từ (1) và (2) ta được BE = CF.
Câu 10:
xứng với D qua AB, điểm N đối xứng với D qua AC. Muốn cho điểm M và N đối xứng qua A thì tam giác ABC phải có điều kiện gì?
 Xem đáp án
Xem đáp án
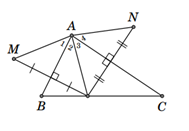
Vì M và D đối xứng qua AB nên AM = AD và .
Vì N và D đối xứng qua AC nên AN = AD và .
Suy ra AM = AN (= AD) và M và N đối xứng nhau qua A
(vì đã có AM = AN)
vuông tại A.
Câu 11:
 Xem đáp án
Xem đáp án
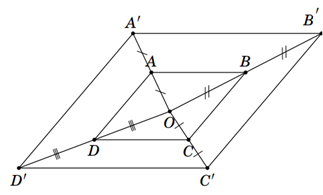
Dùng định lí đường trung bình của tam giác để chứng minh và .
Khi đó A'B'C'D' là hình bình hành, và do đó nó có một tâm đối xứng là giao điểm hai đường chéo.
Câu 12:
Các câu sau đúng hay sai?
a) Tâm đối xứng của một đường thẳng là điểm bất kì của đường thẳng đó.
 Xem đáp án
Xem đáp án
a) Đúng, vì nếu lấy một điểm O bất kì trên đường thẳng thì nó chia đường thẳng đó thành hai và với bất kì một điểm M, trên tia này cũng luôn có một điểm M' đối xứng với nó qua O trên tia kia.
Câu 13:
b) Trọng tâm của một tam giác là tâm đối xứng của tam giác đó.
 Xem đáp án
Xem đáp án
b) Sai,
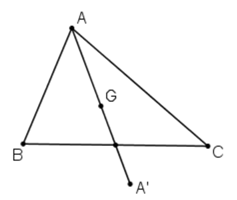
Giả sử tam giác ABC có trọng tâm G.
Khi đó điểm A’ đối xứng với A qua G không nằm trong tam giác.
Câu 14:
c) Hai tam giác đối xứng với nhau qua một điểm thì có chu vi bằng nhau.
 Xem đáp án
Xem đáp án
c) Đúng, vì hai tam giác đối xứng với nhau qua một điểm thì chúng bằng nhau.
Do đó chu vi của chúng bằng nhau.
