10 câu hỏi trắc nghiệm thuộc Dạng 2. Đề số 2 có đáp án

Bài tập Toán 8 Chủ đề 18: Đề kiểm tra chương I có đáp án

Dạng 2. Đề số 2 có đáp án

813 lượt thi
10 câu hỏi
45 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Điền Đ (đúng) hoặc S (sai) trong các phát biểu sau:

1. Độ dài đường trung bình của hình thang bằng nửa tổng độ dài hai cạnh hình thang.

Xem đáp án

Sai

Câu 2:

3. Hình thoi có 2 đường chéo vuông góc với nhau là hình vuông.

Xem đáp án

Sai

Câu 3:

4. Hai đường chéo của hình vuông là trục đối xứng của hình vuông.

Xem đáp án

4. Hai đường chéo của hình vuông là trục đối xứng của hình vuông.

Câu 4:

Cho tam giác ABC vuông tại A, kẻ trung tuyến AD (D $\in$ BC), gọi F là trung điểm của AC. Lấy điểm E đối xứng với A qua tâm D.

a) Tứ giác ABEC là hình gì? Vì sao?

Xem đáp án

a) Ta chứng minh ABEC là hình bình hành mà có Â = 90⁰ => tứ giác ABEC là hình chữ nhật.

Câu 5:

b) Gọi G là trung điểm của DC. Tính độ dài FG, biết BC = 8cm.

Xem đáp án

b) Áp dụng định lý về đường trung bình của tam giác

△ A D C \Rightarrow F G = \frac{1}{2} A D = 2 c m

Câu 6:

c) Tìm điều kiện của tam giác ABC để tứ giác ABEC là hình vuông.

Xem đáp án

c) Để tứ giác ABEC là hình vuông thì AB = AC => $△$ DABC phải là tam giác vuông cân tại A.

Câu 7:

Cho hình chữ nhật ABCD, O là giao điểm hai đường chéo. M thuộc CD và N thuộc AB sao cho DM = BN.

a) Chứng minh ANCM là hình bình hành, từ đó suy ra các điểm M, O, N thẳng hàng.

Xem đáp án

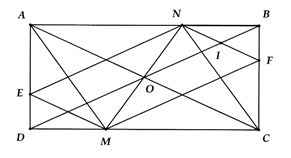
Cho hình chữ nhật ABCD, O là giao điểm hai đường chéo. a) Chứng minh ANCM là hình bình hành, từ đó suy ra các điểm M, O, N thẳng hàng. (ảnh 1)

a) Ta chứng minh $\{\begin{cases} A N = C M \\ A N ∥ C M \end{cases} \Rightarrow A M C N$ là hình bình hành.

Vì O là giao điểm của hai đường chéo AC và MN của hình bình hành AMCN => O $\in$ MN => M, O, N thẳng hàng.

Câu 8:

b) Qua M kẻ đuờng thẳng song song vói AC cắt AD ở E, qua N kẻ đường thẳng song song với AC cắt BC ở F. Chứng minh EN = EM và EN // FM.

Xem đáp án

b) Chứng minh $△$ EMD = $△$ FND (c - g - c) => EM = NF. Từ đó chứng minh được EMFN là hình bình hành => $\{\begin{cases} E N = F M \\ E N ∥ F M \end{cases}$

Câu 9:

c) Tìm vị trí của điểm M, N để ANCM là hình thoi.

Xem đáp án

c) Tứ giác ANCM là hình thoi <=> AC $⊥$ MN tại O => M, N lần lượt là giao điểm của đường thẳng đi qua O, vuông góc AC và cắt CD, AB.

Khi đó M và N là trung điểm của CD và AB.

Câu 10:

d) BD cắt NF tại I. Chứng minh I là trung điểm của NF.

Xem đáp án

d) Ta chứng minh được $△$ BOC cân tại $O \Rightarrow \hat{O C B} = \hat{O B C}$ mà $\hat{N F B} = \hat{O C F}$ (đv) => $△$ BFI cân tại I => IB = IF (1)

Ta lại chứng minh được DNIB cân tại I => IN = IB (2)

Từ (1) và (2) => I là trung điểm của NF.

Bắt đầu thi ngay