Đề thi Học kì 2 Toán lớp 8 cực hay, có đáp án (Tự Luận - Trắc nghiệm - Đề 1)
-
5393 lượt thi
-
12 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 8:
ΔABC đồng dạng với Δ DEF theo tỉ số đồng dạng ;ΔDEF đồng dạng với ΔGHK theo tỉ số đồng dạng . ΔABC đồng dạng với Δ GHK theo tỉ số :
Xem đáp án
Chọn D
Câu 9:
Giải phương trình và bất phương trình sau:
Xem đáp án
a) |3x| = x + 6 (1)
Ta có 3x = 3x khi x ≥ 0 và 3x = -3x khi x < 0
Vậy để giải phương trình (1) ta quy về giải hai phương trình sau:
+ ) Phương trình 3x = x + 6 với điều kiện x ≥ 0
Ta có: 3x = x + 6 ⇔ 2x = 6 ⇔ x = 3 (TMĐK)
Do đó x = 3 là nghiệm của phương trình (1).
+ ) Phương trình -3x = x + 6 với điều kiện x < 0
Ta có -3x = x + 6 ⇔ -4x + 6 ⇔ x = -3/2 (TMĐK)
Do đó x = -3/2 là nghiệm của phương trình (1).
Vậy tập nghiệm của phương trình đã cho S = {3; -3/2}
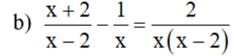
ĐKXĐ: x ≠ 0, x ≠ 2
Quy đồng mẫu hai vễ của phương trình, ta được:
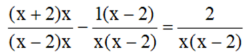
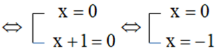
Vậy tập nghiệm của phương trình là S = {-1}
c) (x + 1)(2x – 2) – 3 > –5x – (2x + 1)(3 – x)
⇔ 2x2 – 2x + 2x – 2 – 3 > –5x – (6x – 2x2 + 3 – x)
⇔ 2x2 – 5 ≥ –5x – 6x + 2x2 – 3 + x
⇔ 10x ≥ 2 ⇔ x ≥ 1/5
Tập nghiệm: S = {x | x ≥ 1/5}
Câu 10:
Một tổ sản xuất theo kế hoạch mỗi ngày phải sản xuất 50 sản phẩm. Khi thực hiện mỗi ngày tổ sản xuất 57 sản phẩm. Do đó, tổ đã hoàn thành trước kế hoạch 1 ngày và còn vượt mức 13 sản phẩm. Hỏi theo kế hoạch, tổ phải sản xuất bao nhiêu sản phẩm?
Xem đáp án
Gọi số sản phẩm theo kế hoạc tổ sản xuất là x (sản phẩm)
Điều kiện: x nguyên dương, x > 57
Thời gian dự dịnh theo kế hoạch là: x/50 (ngày)
Số sản phẩm về sau là: x + 13 (sản phẩm)
Thời gian thực tế tổ sản xuất là:
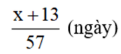
Theo đề ta có phương trình:
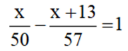
⇔ 57x - 50(x + 13) = 2850
⇔ 57x - 50x - 650 = 2850
⇔ 7x = 3500 ⇔ x = 500 (TMĐK)
Vậy theo kế hoạch tổ sản xuất là 500 sản phẩm.
Câu 11:
Chứng minh rằng nếuthì
Xem đáp án
Ta có:
⇔ a(b + c) < (a + c)b
(vì a > 0, b > 0 và c > 0 ⇔ b + c > 0 và a + c > 0)
⇔ ab + ac < ab + bc
⇔ ac < bc ⇔ a < b (luôn đúng, theo gt)
Câu 12:
Cho tam giác nhọn ABC, các đường cao AD, BE, CF cắt nhau tại H.
a) Chứng minh ΔAEB và ΔAFC đồng dạng. Từ đó suy ra:
b) Chứng minh
c) Cho Chứng minh rằng
d) Chứng minh
Xem đáp án
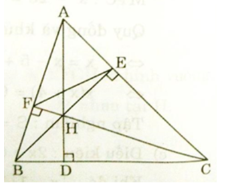
a) Xét ΔAEB và ΔAFC có:
∠AEB = ∠AFC = 90o (gt)
∠A chung
Vậy ΔAEB ∼ ΔAFC (g.g)
b) Xét ΔAEF và ΔABC có
∠A chung
AF.AB = AE.AC (Cmt)
⇒ ΔAEF ∼ ΔABC (c.g.c)
⇒ ∠AEF = ∠ABC
c) ΔAEF ∼ ΔABC (cmt)
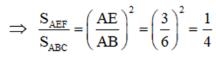
