Trắc nghiệm chuyên đề Toán 8 Chủ đề 2: Kiểm tra học kì 2_ đề số 2 có đáp án
-
1511 lượt thi
-
7 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Giải phương trình sau đây :
8( 3x - 2 ) - 14x = 2( 4 – 7x ) + 15x
Xem đáp án
8( 3x - 2 ) - 14x = 2( 4 – 7x ) + 15x
⇔ 24x – 16 -14x = 8 – 14x + 15x
⇔ 10x -16 = 8 + x
⇔ 9x = 24
⇔ x = 24/9
Câu 2:
Giải phương trình sau đây :
( 3x – 1 )( x – 3 ) – 9 + x2 = 0
Xem đáp án
( 3x – 1 )( x – 3 ) – 9 + x2 = 0
⇔ (3x -1)( x – 3) + (x - 3)( x + 3) = 0
⇔ (x - 3)(3x - 1 + x - 3) = 0
⇔ (x - 3)(4x - 4) = 0
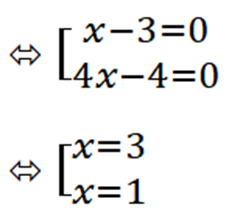
Câu 3:
Giải phương trình sau đây :
|x-2| = 2x-3
Xem đáp án
x - 2| = 2x - 3
TH1: x - 2 ≥ 0 ⇔ x ≥ 2
Khi đó: x - 2 = 2x – 3
⇔ 2x – x = -2 + 3
⇔ x = 1 (không TM điều kiện x ≥ 2)
TH2: x – 2 < 0 ⇔ x < 2
Khi đó: x-2 = -(2x – 3)
⇔ x – 2 = -2x + 3
⇔ 3x = 5
⇔ x = 5/3 ( TM điều kiện x < 2Câu 4:
Giải bất phương trình sau đây và biểu diễn tập nghiệm trên trục số :
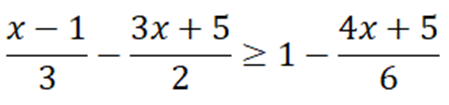
Xem đáp án
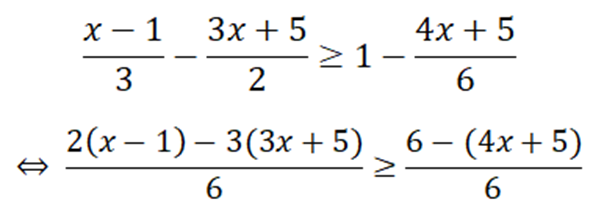
⇔ 2x - 2 - 9x - 15 ≥ 6 - 4x - 5
⇔ 2x - 9x + 4x ≥ 6 - 5 + 2 + 15
⇔ -3x ≥ 18
⇔ x ≤ -6
Vậy tập nghiệm của phương trình là S= {x|x ≤ -6}
Biểu diễn nghiệm trên trục số:
Câu 5:
Tìm giá trị lớn nhất của A = -x2 + 2x + 9
Xem đáp án
A = -x2 + 2x + 9 = -(x2 – 2x + 1) + 10 = - (x + 1)2 + 10
Ta có: - (x + 1)2 ≤ 0 ∀x
- (x + 1)2 + 10 ≤ 10
Dấu bằng xảy ra khi (x + 1)2 = 0 ⇔ x = -1
Vậy GTLN của A là 10, đạt được khi x = -1
Câu 6:
Một người đi xe máy dự định đi từ A đến B với vận tốc 36km/h. Nhưng khi thực hiện người ấy giảm vận tốc 6km/h nên đã đến B chậm hơn dự định là 24 phút. Tính quãng đường AB
Xem đáp án
Gọi quãng đường AB là x (km) (x > 0)
Thời gian người đó dự định đi là: x/36 (km)
Vận tốc đi thực tế là: 36 – 6 = 30 (km)
Thời gian thực tế người đó đi là: x/30 (km)
Do đến B chậm hơn dự tính 24’ = 2/5 h nên ta có phương trình:
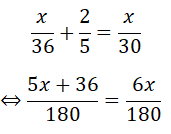
⇔ 5x + 36 = 6x
⇔ x = 36
Vậy quãng đường AB là 36 km.
Câu 7:
Cho tam giác ABC vuông tại A có AH là đường cao. Vẽ HD ⊥ AB ( D ∈ AB ). HE ⊥ AC ( E ∈ AC ). AB = 12cm, AC = 16 cm
a) Chứng minh : ΔHAC ∼ ΔABC
b) Chứng minh : AH2 = AD.AB
c) Chứng minh : AD.AB = AE.AC.
Xem đáp án
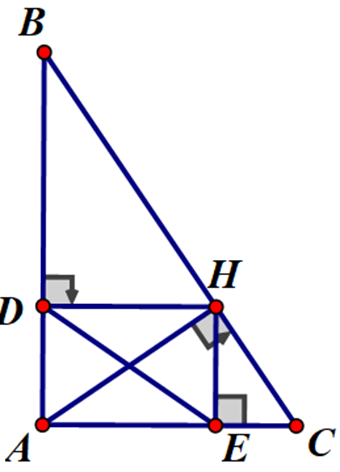
a) Xét ΔHAC và ΔABC có:
∠(ACH ) là góc chung
∠(BAC)= ∠(AHC) = 90o
⇒ ΔHAC ∼ ΔABC (g.g)
b) Xét ΔHAD và ΔBAH có:
∠(DAH ) là góc chung
∠(ADH) = ∠(AHB) = 90o
⇒ ΔHAD ∼ ΔBAH (g.g)
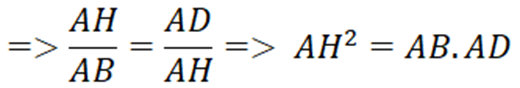
c) Tứ giác ADHE có 3 góc vuông ⇒ ADHE là hình chữ nhật.
⇒ ΔADH= ΔAEH ( c.c.c) ⇒ ∠(DHA)= ∠(DEA)
Mặt khác: ΔHAD ∼ ΔBAH ⇒ ∠(DHA)= ∠(BAH)
∠(DEA)= ∠(BAH)
Xét ΔEAD và ΔBAC có:
∠(DEA)= ∠(BAH)
∠(DAE ) là góc chung
ΔEAD ∼ ΔBAC (g.g)
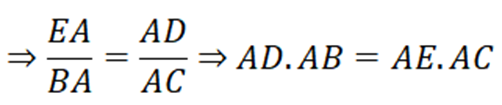
d) ΔEAD ∼ ΔBAC
