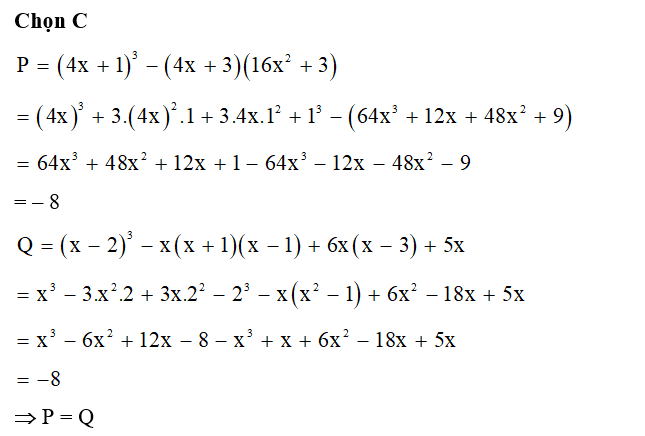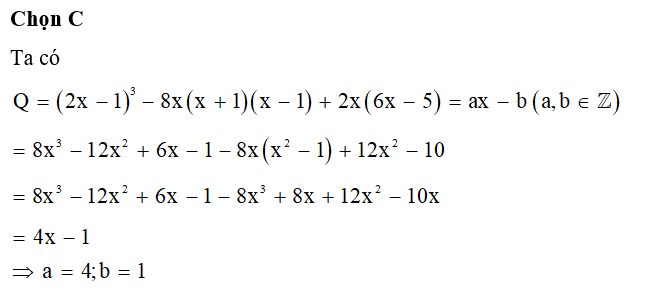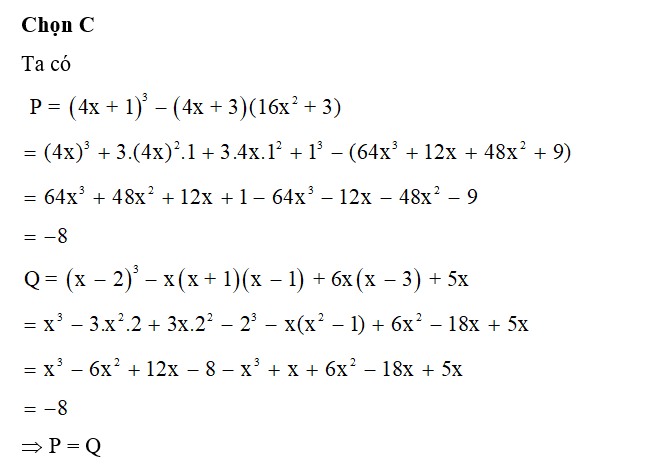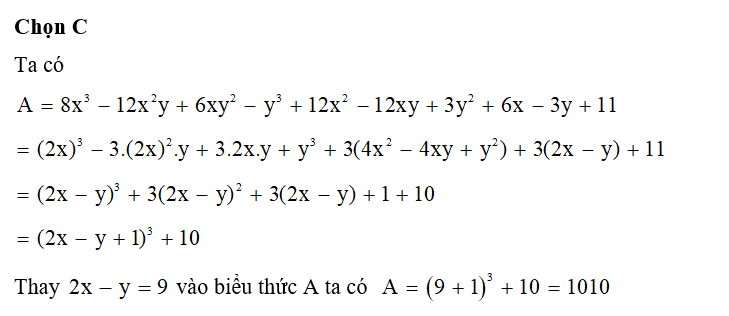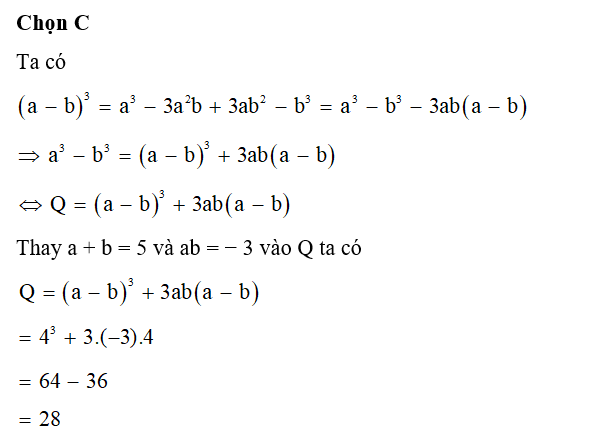15 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán 8 KNTT Bài 7. Lập phương của một tổng. Lập phương của một hiệu có đáp án

Trắc nghiệm Toán 8 KNTT Bài 7. Lập phương của một tổng. Lập phương của một hiệu có đáp án

Đề số 1

Trắc nghiệm Toán 8 KNTT Bài 7. Lập phương của một tổng. Lập phương của một hiệu có đáp án

197 lượt thi
15 câu hỏi
60 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Chọn câu đúng?

A. ${(A + B)}^{3} {= A}^{3} {+ 3A}^{2} {B + 3AB}^{2} {+ B}^{3}$

B. ${(A - B)}^{3} {=A}^{3} - {3A}^{2} B - {3AB}^{2} - B^{3}$

C. ${(A + B)}^{3} {= A}^{3} {+ B}^{3}$

{(A - B)}^{3} {= A}^{3} {- B}^{3}

Xem đáp án

Đáp án đúng là: A

${(A + B)}^{3} {= A}^{3} {+ 3A}^{2} {B + 3AB}^{2} {+ B}^{3}$

Câu 2:

Viết biểu thức $x^{3} + 3 x^{2} + 3 x + 1$ dưới dạng lập phương của một tổng

A. ${(x + 1)}^{3}$

B. ${(x + 3)}^{3}$

C. ${(x - 1)}^{3}$

{(x - 3)}^{3}

Xem đáp án

Đáp án đúng là: A

$x^{3} {+ 3x}^{2} + 3x + 1 = {(x + 1)}^{3}$

Câu 3:

Khai triển hằng đẳng thức ${(x - 2)}^{3}$ ta được

A. $x^{3} - {6x}^{2} + 12x - 8$

B. $x^{3} {+6x}^{2} + 12x+8$

C. $x^{3} {- 6x}^{2} - 12x-8$

x^{3} {+ 6x}^{2} - 12x + 8

Xem đáp án

Đáp án đúng là: A

${(x - 2)}^{3} {= x}^{3} - {3.x}^{2} {.2 + 3.x.2}^{2} - 2^{3} {= x}^{3} - {6x}^{2} + 12x - 8$

Câu 4:

Cho $A + \frac{3}{4} x^{2} - \frac{3}{2} x + 1 = {(B + 1)}^{3}$ . Khi đó

A. $A = - \frac{x^{3}}{8}; B = \frac{x}{2}$

B. $A = - \frac{x^{3}}{8}; B = - \frac{x}{2}$

C. $A = - \frac{x^{3}}{8}; B = - \frac{x}{8}$

A = \frac{x^{3}}{8}; B = \frac{x}{8}

Xem đáp án

Đáp án đúng là: B

$= {(- \frac{1}{2} x)}^{3} + 3. {(- \frac{1}{2} x)}^{2} .1 + 3. (- \frac{1}{2} x) {.1}^{2} + 1^{3} = {(- \frac{x}{2} + 1)}^{3}$

$\Rightarrow A = {(- \frac{1}{2} x)}^{3} = - \frac{x^{3}}{8}; B = - \frac{1}{2} x = - \frac{x}{2}$

Vậy P là một số chẵn.

Câu 5:

Viết biểu thức $8 - 36 x + 54 x^{2} - 27 x^{3}$ dưới dạng lập phương của một tổng hoặc một hiệu ta được

A. ${(3 x + 2)}^{3}$

B. ${(2 - 3 x)}^{3}$

C. ${(8 - 27 x)}^{3}$

{(3 x - 2)}^{3}

Xem đáp án

Đáp án đúng là: B

$8 - 36 x + 54 x^{2} - 27 x^{3} = 2^{3} - {3.2}^{2} . (3 x) + 3.2. {(3 x)}^{2} - {(3 x)}^{3} = {(2 - 3 x)}^{3}$

Câu 6:

Kết quả phép nhân: $(x^{2} - 2 x + 1) (x - 1) =$

A. $x^{3} - 3 x^{2} + 3 x + 1$

B. $x^{3} + 3 x^{2} + 3 x - 1$ ;

C. $x^{3} - 3 x^{2} + 3 x - 1$ ;

x^{3} + 3 x^{2} + 3 x - 1

Xem đáp án

Đáp án đúng là: C

Ta có: $(x^{2} - 2 x + 1) (x - 1) = {(x - 1)}^{2} (x - 1)$

$= {(x - 1)}^{3} = x^{3} - 3 x^{2} + 3 x - 1.$

Câu 7:

Cho biểu thức

H = (x + 5) (x^{2} - 5 x + 25) - {(2 x + 1)}^{3} + 7 {(x - 1)}^{3} - 3 x (- 11 x + 5)

. Khi đó

A. H là một số chia hết cho 12.

B. H là một số chẵn.

C. H là một số lẻ.

D. H là một số chính phương.

Xem đáp án

Đáp án đúng là: C

$H = (x + 5) (x^{2} - 5 x + 25) - {(2 x + 1)}^{3} + 7 {(x - 1)}^{3} - 3 x (- 11 x + 5)$

$H = (x + 5) (x^{2} - 5 x + 25) - {(2 x + 1)}^{3} + 7 {(x - 1)}^{3} - 3 x (- 11 x + 5) + 7 (x^{3} - 3 x^{2} + 3 x - 1) + 33 x^{2} - 15 x$

$= x^{3} + 125 - 8 x^{3} - 12 x^{2} - 6 x - 1 + 7 x^{3} - 21 x^{2} + 21 x - 7 + 33 x^{2} - 15 x$

$= (x^{3} - 8 x^{3} + 7 x^{3}) + (- 12 x^{2} - 21 x^{2} + 33 x^{2}) + (5^{3} - 1 - 7)$

= 117

Vậy H là một số lẻ.

Câu 8:

Tính giá trị của biểu thức $M = {(x + 2 y)}^{3} - 6 {(x + 2 y)}^{2} + 12 (x + 2 y) - 8$ tại x = 20, y = 1

A. 4000

B. 6000

C. 8000

D. 2000

Xem đáp án

Đáp án đúng là: C

$M = {(x + 2 y)}^{3} - 6 {(x + 2 y)}^{2} + 12 (x + 2 y) - 8$

$= {(x + 2 y)}^{3} - 3. {(x + 2 y)}^{2} .2 + 3. (x + 2 y) {.2}^{2} - 2^{3}$ '

$= {(x + 2 y - 2)}^{3}$

Thay x = 20, y = 1 vào biểu thức M ta có $M = {(20 + 2.1 - 2)}^{3} = 20^{3} = 8000$

Câu 9:

Cho hai biểu thức

$P = {(4 x + 1)}^{3} - (4 x + 3) (16 x^{2} + 3);$

$Q = {(x - 2)}^{3} - x (x + 1) (x - 1) + 6 x (x - 3) + 5 x .$

Tìm mối quan hệ giữa hai biểu thức P, Q?

A. P = – Q

B. P = 2Q

C. P = Q

P = \frac{1}{2} Q

Xem đáp án

Cho hai biểu thức P= ( 4x+1 ) 63 - ( 4x+ 3) ( 16x^2 + 3) (ảnh 1)

Câu 10:

Rút gọn biểu thức $P = 8 x^{3} - 12 x^{2} y + 6 x y^{2} - y^{3} + 12 x^{2} - 12 x y + 3 y^{2} + 6 x - 3 y + 11$ ta được

A. $P = {(2x - y - 1)}^{3} + 10$

B. $P = {(2x+y - 1)}^{3} + 10$

C. $P = {(2 x - y + 1)}^{3} + 10$

P = {(2 x - y- 1)}^{3} - 10

Xem đáp án

Đáp án đúng là: C

$P = 8 x^{3} - 12 x^{2} y + 6 x y^{2} - y^{3} + 12 x^{2} - 12 x y + 3 y^{2} + 6 x - 3 y + 11$

$= {(2 x - y)}^{3} + 3 {(2 x - y)}^{2} + 3 (2 x - y) + 1 + 10$

$= {(2 x - y + 1)}^{3} + 10$

Câu 11:

Cho biết $Q = {(2 x - 1)}^{3} - 8 x (x + 1) (x - 1) + 2 x (6 x - 5) = ax - b (a, b \in ℤ)$ . Khi đó

A. a = – 4; b = 1

B. a = 4; b = – 1

C. a = 4; b = 1

D. a = – 4; b = – 1

Xem đáp án

Cho biết Q= (2x-1) ^3- 8x (x +1 ) ( x-1) + 2x ( 6x -5) = ax - b ( a,b thuộc Z). Khi đó (ảnh 1)

Câu 12:

Cho hai biểu thức $P = {(4x + 1)}^{3} - (4x + 3) {(16x}^{2} + 3);$ $Q = {(x - 2)}^{3} - x (x + 1) (x - 1) + 6x (x - 3) + 5x$ . So sánh P và Q?

A. P < Q

B. P = –Q

C. P = Q

D. P > Q

Xem đáp án

Cho hai biểu thức P= ( 4x+ 1)- ( 1x+ 3) ( 16x^2+ 3) ; Q= ( x-2 ) 63 -x( x+1) (x-1)+ 6x( x-3 ) + 5x . So sánh P và Q? (ảnh 1)

Câu 13:

Cho $2 x - y = 9$ . Giá trị của biểu thức $A = 8 x^{3} - 12 x^{2} y + 6 x y^{2} - y^{3} + 12 x^{2} - 12 x y + 3 y^{2} + 6 x - 3 y + 11$ là

A. A = 1001

B. A = 1000

C. A = 1010

D. A = 900

Xem đáp án

Cho 2x-y=9. Giá trị của biểu thức A= 8x^3 -12 x62 y+ 6xy^2-y^3+ 12x^2 -12xy+ 3y^2+6x-3y+11 là (ảnh 1)

Câu 14:

Giá trị của biểu thức $Q = a^{3} - b^{3}$ biết $a - b = 4$ và $a b = - 3$ là

A. Q = 100

B. Q = 64

C. Q = 28

D. Q = 36

Xem đáp án

Giá trị của biểu thức Q= a^3 -b biết a-b=4 và ab= -3 là (ảnh 1)

Câu 15:

Cho a + b + c = 0 . Giá trị của biểu thức $B = a^{3} + b^{3} + c^{3} - 3 a b c$

A. B = 0

B. B = 1

C. B = – 1

D. Không xác định được.

Xem đáp án

Đáp án đúng là: A

${(a + b)}^{3} = a^{3} + 3 a^{2} b + 3 a b^{2} + b^{3} = a^{3} + b^{3} + 3 a b (a + b)$

$\Rightarrow a^{3} + b^{3} = {(a + b)}^{3} - 3 a b (a + b)$

Ta có

$B = a^{3} + b^{3} + c^{3} - 3 a b c$

$= {(a + b)}^{3} - 3 a b (a + b) + c^{3} - 3 a b c$

$= {(a + b)}^{3} + x^{3} - 3 a b (a + b + c)$

Tương tự, ta có ${(a + b + c)}^{3} - 3 (a + b) c (c + b + c)$

$\Leftrightarrow B = {(a + b + c)}^{3} - 3 (a + b) c (a + b + c) - 3 a b (a + b + c)$

Mà a + b + c = 0 nên $B = 0 - 3(a + b)c.0 - 3ab.0 = 0$ .

Bắt đầu thi ngay