7 câu hỏi trắc nghiệm thuộc Bài tập theo tuần Toán 8 - Tuần 11 (Phân thức đại số) - vietjack.online

Bài tập theo tuần Toán 8 - Tuần 11

Bài tập theo tuần Toán 8 - Tuần 11 (Phân thức đại số)

1410 lượt thi
7 câu hỏi
45 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Dùng định nghĩa, chứng tỏ 2 phân thức bằng nhau:

\frac{7 y}{9} = \frac{49 xy}{63 x}

$\frac{7 y}{9} = \frac{49 xy}{63 x} vì 7 y .63 x = 49 xy .9 = 441 xy$

Câu 2:

Dùng định nghĩa, chứng tỏ 2 phân thức bằng nhau:

\frac{2 x (x + 4)}{8 xy (x + 4)} = \frac{1}{4 y}

$\frac{2 x (x + 4)}{8 xy (x + 4)} = \frac{1}{4 y} vì 2 x (x + 4) .4 y = 8 xy (x + 4) .1 = 8 xy (x + 4)$

Câu 3:

Dùng định nghĩa, chứng tỏ 2 phân thức bằng nhau:

\frac{x^{3} + 27}{x^{2} - 3 x + 9} = x + 3

$\frac{x^{3} + 27}{x^{2} - 3 x + 9} = x + 3 do (x + 3) (x^{2} - 3 x + 9) = x^{3} + 27$

Câu 4:

Cho hai phân thức

\frac{P}{Q}

\frac{R}{S}

Chứng minh rằng: Nếu

\frac{P}{Q} = \frac{R}{S} \Rightarrow \frac{P + Q}{Q} = \frac{R + S}{S}

$\frac{P}{Q} = \frac{R}{S} \Rightarrow \frac{P}{Q} + 1 = \frac{R}{S} + 1 \Rightarrow \frac{P + Q}{Q} = \frac{R + S}{S}$

Câu 5:

Tìm đa thức M thỏa mãn:

\frac{(x + 3) M}{x - 3} = \frac{x - 1}{x^{2} - 9}

$\begin{array}{l} \frac{(x + 3) M}{x - 3} = \frac{x - 1}{x^{2} - 9} \Rightarrow M (x + 3) (x^{2} - 9) = (x - 1) (x - 3) \\ M = \frac{(x - 1) (x - 3)}{(x + 3) (x - 3) (x + 3)} = \frac{x - 1}{{(x + 3)}^{2}} \end{array}$

Câu 6:

Cho hình vuông DEBC. Trên cạnh CD lấy điểm A, trên tia đối của tia DC lấy điểm K, trên tia đối của tia ED lấy M sao cho CA = DK = EM. Vẽ hình vuông

DKIH (H \in DE)

. Chứng minh rằng

ABMI

là hình vuông ?

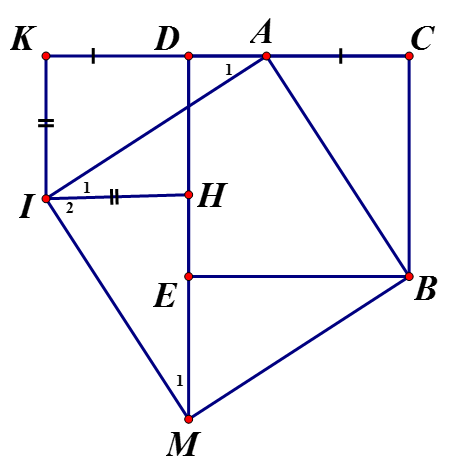
Cho hình vuông DEBC Trên cạnh CD lấy điểm A, trên tia đối của tia DC lấy điểm K, (ảnh 1)

Ta có: $\hat{A_{1}} = \hat{I_{1}}$ (so le trong) (1), Xét $ΔAKI và ΔMHI$

Có: $AK = MH, \hat{K} = \hat{H} = 90^{0}, KI = HI \Rightarrow ΔAKI = ΔMHI (cgc) \Rightarrow \hat{A_{1}} = \hat{M_{1}} (2)$

Từ (1) và (2) suy ra $\hat{I_{1}} = \hat{M_{1}}$ mà $\hat{M_{1}} + \hat{I_{2}} = 90^{0}$ (phụ nhau) nên $\hat{I_{1}} + \hat{I_{2}} = \hat{AIM} = 90^{0} (a)$

Chứng minh tương tự $\Rightarrow \hat{IMB} = \hat{MBA} = 90^{0} (b)$

Từ (a) và (b) $\Rightarrow AIMB$ có 3 góc vuông nên là hình chữ nhật mà $AI = MI (do ΔAKI = ΔMHI)$

Nên AIMB là hình vuông.

Câu 7:

Cho tam giác ABC cân tại A, đường trung tuyến

AD (D \in BC) .

Gọi E, F thứ tự là trung điểm của AB, AC.

a) Chứng minh AEDF là hình bình hành

b) M đối xứng với D qua F. Tứ giác ADCM là hình gì ?

c) Tìm điều kiện của

ΔABC

để ADCM là hình vuông.

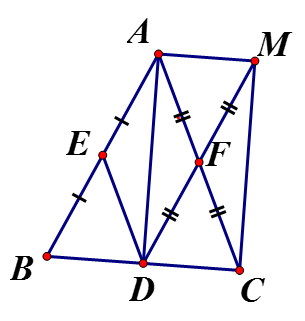
Cho tam giác ABC cân tại A, đường trung tuyến AD (D thuộc BC) Gọi E, F thứ tự là trung điểm của AB, AC (ảnh 1)

a) Sử dụng đường trung bình ta có ED là đường trung bình

ΔABC \Rightarrow ED = \frac{1}{2} AC = AF

ED / / AC \Rightarrow ED / / AF \Rightarrow AEDF

là hình bình hành

b) Tứ giác ADCM có hai đường chéo cắt nhau tại trung điểm F mỗi đường nên AMCD là hình bình hành và

AD ⊥ BC

(do

ΔABC

cân AD đường trung tuyến cũng là đường cao)

\Rightarrow \hat{ADC} = 90^{0} \Rightarrow ADCM

là hình chữ nhật

c) ADCM là hình vuông <=> AC là phân giác

\Rightarrow \hat{MAC} = \hat{CAD} = \hat{DAB} = 45^{0}

\Rightarrow \hat{CAD} + \hat{DAB} = \hat{CAB} = 45^{0} + 45^{0} = 90^{0} \Rightarrow ΔABC

vuông cân tại A

Vậy

ΔABC

vuông cân tại A thì AMCD là hình vuông

Bắt đầu thi ngay

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương