7 câu hỏi trắc nghiệm thuộc Bài tập theo tuần Toán 8 - Tuần 13 (đề 1) - vietjack.online

Bài tập theo tuần Toán 8 - Tuần 13

Bài tập theo tuần Toán 8 - Tuần 13 (đề 1)

1384 lượt thi
7 câu hỏi
45 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Hình nào sau đây vừa có tâm đối xứng, vừa có trục đối xứng ?

A. Hình bình hành

B. Hình thang vuông

C. Hình thoi

D. Hình thang cân

Đáp án C

Câu 2:

Trong các phát biểu sau, phát biểu nào sai

A. Hình bình hành có 1 trục đối xứng

B. Đoạn thẳng có 2 trục đối xứng

C. Hình vuông có 4 trục đối xứng

D. Tam giác cân có 1 trục đối xứng

Đáp án A

Câu 3:

Tứ giác ABCD là hình vuông nếu

A. ABCD là hình bình hành có AB = AD

B. ABCD là hình chữ nhật có

AC ⊥ BD

C. ABCD là hình thoi có AC là tia phân giác góc A

D. Cả 3 trường hợp trên đều đúng

Đáp án B

Câu 4:

Độ dài 1 cạnh hình vuông bằng 4cm, thì độ dài đường chéo hình vuông đó là

A. 16cm

B. 8cm

C. $4 \sqrt{2}$ cm

D. 4cm

Đáp án C

Câu 5:

Đoạn thẳng MN là ………………………………………........

Cho $CD = 8 cm, EF = 14 cm .$ Độ dài của MN bằng

A. 22cm

B. 7cm

C. 4cm

D. 11cm

Đoạn thẳng MN là đường trung bình của hình thang CDEF

Độ dài

MN : D . 11 cm

Câu 6:

Cho tam giác DEF vuông tại D. Biết DE = 3 cm, DF = 4cm.

b) Gọi K là trung điểm của EF. Tính độ dài DK.

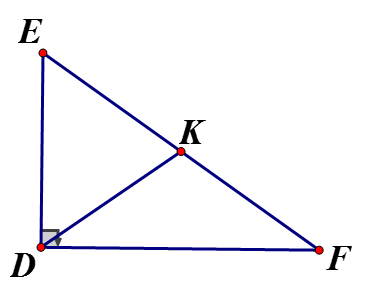
Cho tam giác DEF vuông tại D. Biết DE = 3 cm, DF = 4cm. a) Tính EF (ảnh 1)

a) Áp dụng định lý Pytago vào $ΔDEF$ vuông tại D $\Rightarrow {EF}^{2} = {DE}^{2} + {DF}^{2}$

Hay ${EF}^{2} = 3^{2} + 4^{2} = 25 \Rightarrow EF = \sqrt{25} = 5 (cm)$

b) $ΔDEF$ vuông tại D, có DK là đường trung tuyến $\Rightarrow DK = \frac{1}{2} EF = \frac{1}{2} .5 = 2, 5 (cm)$

Câu 7:

Cho tam giác ABC cân tại A, đường trung tuyến AM

(M \in BC)

. Gọi I, K thứ tự là trung điểm của AB và AC.

a) Chứng minh tứ giác IMCK là hình bình hành

b) Gọi H là điểm đối xứng với M qua điểm K. Hỏi tứ giác AMCH là hình gì? Vì sao?

c) Tìm điều kiện của tam giác ABC để tứ giác AMCH là hình vuông ?

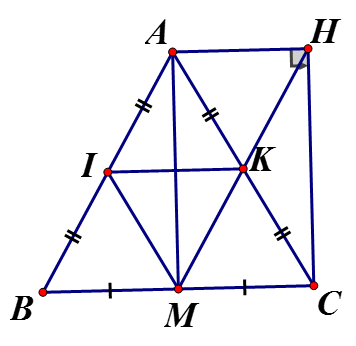
Cho tam giác ABC cân tại A, đường trung tuyến AM (M thuộc BC) . Gọi I, K thứ tự là trung điểm của AB và AC. (ảnh 1)

a) Xét $ΔABC$ có I là trung điểm AB, K là trung điểm $AC \Rightarrow IK$ là đường trung bình $ΔABC \Rightarrow IK / / BC, IK = \frac{1}{2} BC$ mà $M \in BC, MC = \frac{1}{2} BC$

$\Rightarrow \{\begin{cases} IK = MC \\ IK / / MC \end{cases} \Rightarrow IKCM$ là hình bình hành

b) Tứ giác AHCM có 2 đường chéo AC, MH cắt nhau tại trung điểm K mỗi đường

$\Rightarrow AHCM$ là hình bình hành (1)

$ΔABC$ cân tại A nên AM đường trung tuyến cũng là đường cao $\Rightarrow AM ⊥ BC (2)$

Từ (1) và (2) suy ra AHCM là hình chữ nhật

c) AHCM là hình vuông

\Leftrightarrow AM = MC \Rightarrow AM = \frac{1}{2} BC \Rightarrow ΔABC

vuông tại A

(định lý đảo đường trung tuyến ứng với cạnh huyền)

Vậy

ΔABC

vuông cân thì AMCH là hình vuông.

Bắt đầu thi ngay

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương