Bài tập theo tuần Toán 8 - Tuần 7
-
1480 lượt thi
-
30 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 28:
Cho hình bình hành ABCD gọi O là giao điểm hai đường chéo. Qua O vẽ đường thẳng cắt hai cạnh AB, CD ở E, F. Qua O vẽ đường thẳng cắt 2 cạnh AD, BC ở G và H. Chứng minh EFGH là hình bình hành.
 Xem đáp án
Xem đáp án
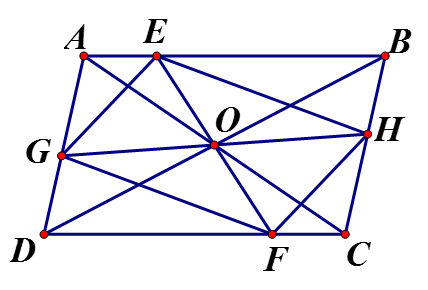
Xét và có:
(đối đỉnh); (so le trong)
Chứng minh tương tự ta có:
Từ (1) và (2) suy ra tứ giác EFGH có hai đường chéo cắt nhau tại trung điểm O mỗi đường nên là EFGH hình bình hành.
Câu 29:
 Xem đáp án
Xem đáp án
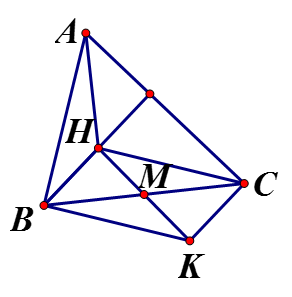
Tứ giác BHCK có hai đường chéo BC, HK cắt nhau tại trung điểm mỗi đường nên BHCK là hình bình hành nên
Ta có: (vì H là trực tâm) mà
Câu 30:
 Xem đáp án
Xem đáp án
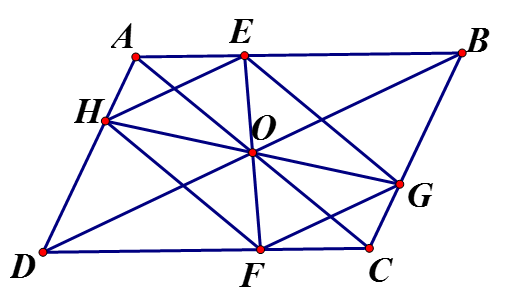
và có: (đối đỉnh); (tính chất hình bình hành)
(so le trong)
Ta có: (cùng // AC), do đó
(tính chất hình bình hành)
Tứ giác EGFH có nên là hình bình hành
Do đó O là trung điểm HG. nên H và G đối xứng nhau qua O.