10 câu hỏi trắc nghiệm thuộc Dạng 2: Phiếu bài luyện số 2 có đáp án

Bài tập Toán 8 Chủ đề 4: Luyện tập hình thang cân có đáp án

Dạng 2: Phiếu bài luyện số 2 có đáp án

1097 lượt thi
10 câu hỏi
45 phút

Danh sách câu hỏi

Câu 1:

\hat{A} = \hat{B} = \hat{C} = 90 °

. Hỏi ABCD có là hình thang cân không? Vì sao?

Xem đáp án

Tứ giác ABCD có góc A = góc B = góc C = 90 độ . Hỏi ABCD có là hình thang cân không? Vì sao? (ảnh 1)

Ta có $\hat{A} + \hat{B} = 90 ° + 90 ° = 180^{0} \Rightarrow A D / / B C$

Do đó tứ giác ABCD là hình thang

Mà

\hat{B} = \hat{C}

nên tứ giác ABCD là hình thang cân

Câu 2:

Cho hình vẽ. Hỏi tứ giác ABCD có là hình thang cân không? Vì sao?

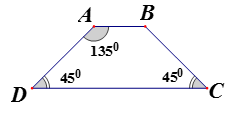
Xem đáp án

Ta có $\hat{A} + \hat{D} = 135 ° + 45 ° = 180^{0} \Rightarrow A B / / D C$

Do đó tứ giác ABCD là hình thang

Mà

\hat{D} = \hat{C} = 45^{0}

nên tứ giác ABCD là hình thang cân

Câu 3:

Cho tam giác ABC cân tại A. Gọi M, N lần lượt là trung điểm của AB, AC. Chứng minh tứ giác MNCB là hình thang cân.

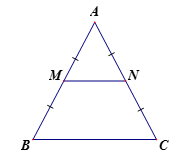
Xem đáp án

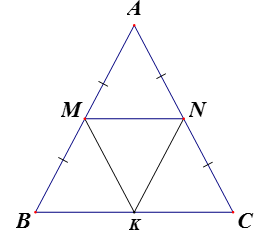
Cho tam giác ABC cân tại A . Gọi M, N lần lượt là trung điểm của AB, AC . Chứng minh tứ giác ,MNCB là hình thang cân. (ảnh 2)

+ Kẻ đường thẳng MK sao cho MK // NC (K thuộc BC), nối N với K.

+ Ta có MK // NC suy ra $\hat{M K B} = \hat{N K C}$ mà $\hat{B} = \hat{C}$ (do tam giác ABC cân) nên $\hat{B} = \hat{M K B}$ . Suy ra $Δ M B K$ là tam giác cân

+ Chứng minh $Δ M B K = Δ A M N$ (c.g.c), suy ra $\hat{A M N} = \hat{A B C}$ , mà 2 góc này ở vị trí đồng vị nên suy ra MN//BC. từ đó suy ra điều phải chứng minh.

Câu 4:

Cho hình thang EFGH (EF//GH).

Biết rằng: $E H = E F = \frac{1}{2} G H$ . Chứng minh tứ giác EFGH là hình thang cân.

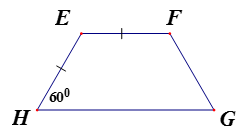
Xem đáp án

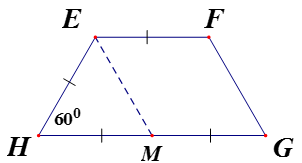
Cho hình thang EFGH (EF//GH). Biết rằng: EH = EF = 1/2GH. Chứng minh tứ giác EFGH là hình thang cân. (ảnh 2)

Lấy M là trung điểm của GH. Chứng minh $Δ E M H$ là tam giác đều.

Từ đó, chứng minh được tứ giác EFGH là hình thang cân.

Câu 5:

Cho hình vẽ. Biết tứ giác ABCD là một hình thang cân. Tính diện tích tứ giác ABCD.

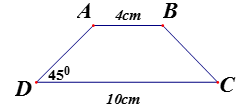
Xem đáp án

Cách 1:

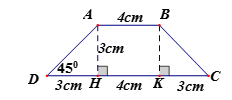
Cho hình vẽ. Biết tứ giác ABCD là một hình thang cân. Tính diện tích tứ giác ABCD. (ảnh 2)

Kẻ thêm các đường vuông góc như hình vẽ, tính được chiều cao hình thang là 3cm.

Từ đó tính diện tích hình thang ABCD bằng (4+10).3:2 = 21 (cm²).

Cách 2

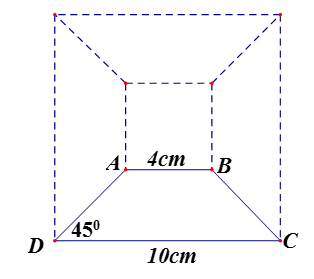
Cho hình vẽ. Biết tứ giác ABCD là một hình thang cân. Tính diện tích tứ giác ABCD. (ảnh 3)

Vẽ thêm các hình thang cân và ghép lại thành 2 hình vuông (như hình vẽ). Từ đó tính được diện tích hình thang cân ABCD bằng (10² – 4²):4 = 21 (cm²).

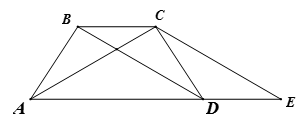
Câu 6:

Cho hình vẽ, biết ABCD là hình thang cân (đáy CB và AD). Từ C kẻ đường thẳng song song với BD cắt AD tại E. Chứng minh tam giác ACE là một tam giác cân.

Xem đáp án

+ Chỉ ra BD = CE

+ Áp dụng tính chất đường chéo hình thang cân suy ra AC = BD. Suy ra CA = CE.

+ Kết luận tam giác ACE là một tam giác cân.

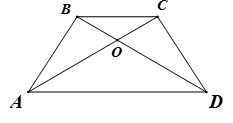
Câu 7:

Cho hình vẽ, biết ABCD là hình thang cân (đáy CB và AD, BC < AD). Hai đường chéo cắt nhau tại điểm O. Chứng minh tam giác OAD là một tam giác cân.

Xem đáp án

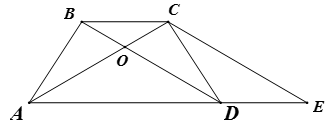
Cho hình vẽ, biết ABCD là hình thang cân (đáy CB và AD, BC < AD). Hai đường chéo cắt nhau tại điểm O. Chứng minh tam giác OAD là một tam giác cân. (ảnh 2)

Kẻ CE // BD (hình vẽ)

+ Chỉ ra tam giác ACE là một tam giác cân.

+ Từ đó suy ra tam giác OAD cân

Câu 8:

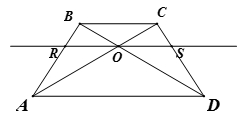
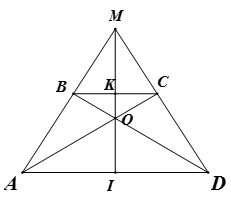
Cho hình vẽ. Biết rằng tứ giác ABCD là hình thang cân. (BC // AD). Đường thẳng đi qua O và song song với hai đáy cắt các cạnh bên AB, CD lần lượt ở R và S. Chứng minh:

a) O là trung điểm của RS.

Xem đáp án

a) Chứng minh các tam giác bằng nhau suy ra OR = OS

Câu 9:

b) $\frac{1}{B C} + \frac{1}{A D} = \frac{2}{R S}$

Xem đáp án

b) Cần sử dụng định lý talet

Câu 10:

Cho hình vẽ. Biết tứ giác ABCD là hình thang cân. Hai đường chéo AC và BD cắt nhau tại O. Hai cạnh bên AB và CD cắt nhau tại M. Chứng minh MK đi qua trung điểm của hai đáy.

Cho hình vẽ. Biết tứ giác ABCD là hình thang cân. Hai đường chéo AC và BD cắt nhau tại O. Hai cạnh bên AB và CD cắt nhau tại M. (ảnh 1)

Xem đáp án

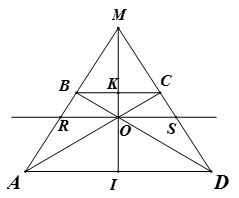
Cho hình vẽ. Biết tứ giác ABCD là hình thang cân. Hai đường chéo AC và BD cắt nhau tại O. Hai cạnh bên AB và CD cắt nhau tại M. (ảnh 2)

+ Chứng minh các tam giác MBC , tam giác MAD và tam giác MRS là các tam giác cân tại M.

+ Ta có O là trung điểm của RS, từ đó suy ra điều phải chứng minh.

Bắt đầu thi ngay