Đề kiểm tra Cuối kì 2 Toán 8 CTST có đáp án (Đề 2)
-
456 lượt thi
-
17 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
Cho hai đường thẳng và Với điều kiện nào sau đây thì hai đường thẳng d và d’ cắt nhau?
 Xem đáp án
Xem đáp án
Chọn đáp án C
Câu 2:
Hàm số bậc nhất có đồ thị là đường thẳng song song với đường thẳng
y = -x + 2 và cắt trục tung tại điểm có tung độ bằng 1 là
 Xem đáp án
Xem đáp án
Chọn đáp án B
Câu 4:
Hai lớp 8A và 8B cùng tham gia trồng cây. Lớp 8A có 40 học sinh, mỗi em trồng được 3 cây. Lớp 8B có 30 học sinh mỗi em trồng x cây. Biết số cây mỗi lớp trồng là như nhau, khi đó giá trị của x là
 Xem đáp án
Xem đáp án
Chọn đáp án C
Câu 7:
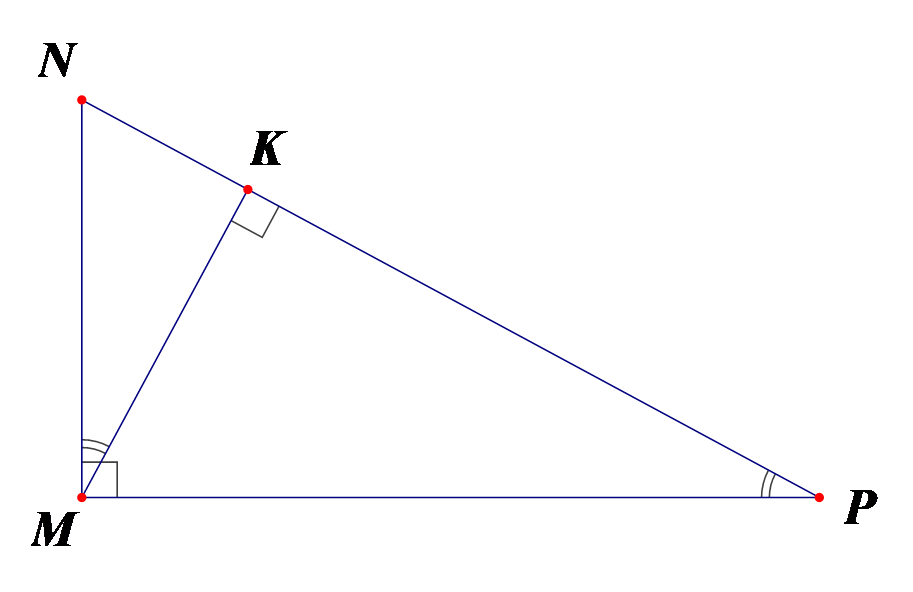
Cho hình vẽ. Cho các khẳng định sau:
(I) .
(II) .
Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Chọn đáp án A
Câu 8:
Trong hộp bút của bạn Hoa có 5 bút bi xanh, 3 bút bi đỏ và 2 bút bi đen. Xác suất thực nghiệm của biến cố “Bạn Hoa lấy một bút bi đỏ” là
 Xem đáp án
Xem đáp án
Chọn đáp án B
Câu 9:
Giải các phương trình sau:
a) ; b) .
 Xem đáp án
Xem đáp án
a)
Vậy nghiệm của phương trình là x = 11.
b)
(vì )
Vậy nghiệm của phương trình là x = 1
Câu 10:
Hai ô tô cùng khởi hành từ hai bến cách nhau 175 km để gặp nhau. Xe thứ nhất đi sớm hơn xe thứ hai là 1 giờ 30 phút với vận tốc 30 km/h. Vận tốc của xe thứ hai là 35 km/h. Hỏi sau mấy giờ hai xe gặp nhau?
 Xem đáp án
Xem đáp án
Gọi thời gian đi của xe 2 là x (giờ) .
Thời gian đi của xe thứ nhất là (giờ).
Quãng đường xe thứ hai đi là: .
Quãng đường xe thứ nhất đi là: .
Vì hai bến cách nhau 175 km nên ta có phương trình:
x = 2 (thỏa mãn điều kiện).
Vậy sau 2 giờ xe thứ hai gặp xe thứ nhất.
Câu 11:
Cho hàm số Tìm m để hàm số đã cho là hàm số bậc nhất.
 Xem đáp án
Xem đáp án
Hàm số là hàm số bậc nhất khi và chỉ khi hay
Câu 12:
Đồng euro (EUR) là đơn vị tiền tệ chính thức ở một số quốc gia thành viên của Liên minh Châu Âu. Vào một ngày, tỉ giá hối đoái giữa đồng euro và đồng đô la Mỹ (USD) là 1 EUR = 1,1052 USD.
a) Viết công thức để chuyển đổi x euro sang y đô la Mỹ. Công thức tính y theo x này có phải là hàm số bậc nhất của x không?
b) Vào ngày đó, 200 euro có giá trị bằng bao nhiêu đô la Mỹ? 500 đô la Mỹ có giá trị bằng bao nhiêu euro?
 Xem đáp án
Xem đáp án
a) Công thức để chuyển đổi x euro sang y đô la Mỹ là y = 1,1052x
Công thức tính y theo x này là hàm số bậc nhất của x vì với mỗi giá trị của x , ta xác định duy nhất một giá trị của y .
b) 200 euro có giá trị là đô la Mỹ.
500 đô la Mỹ có giá trị là euro.
Câu 13:
Một hộp chứa các viên bi màu trắng và đen có kích thước và khối lượng như nhau. Mai lấy ra ngẫu nhiên từ một hộp, xem màu rồi trả lại hộp. Lặp lại thử nghiệm đó 80 lần, Mai thấy có 24 lần lấy được viên bi màu trắng.
a) Hãy tính xác suất thực nghiệm của biến cố "Lấy được viên bi màu đen" sau 80 lần thử.
b) Biết tổng số bi trong hộp là 10, hãy ước lượng xem trong hộp có khoảng bao nhiêu viên bi trắng.
Câu 14:
 Xem đáp án
Xem đáp án
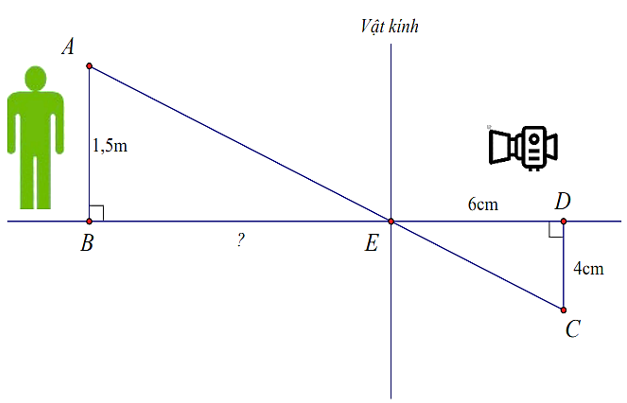
Đổi:
Ta có nên .
Suy ra (theo định lí Thalès).
Do đó .
Vậy người đứng cách vật kính máy ảnh là 225 cmCâu 16:
 Xem đáp án
Xem đáp án
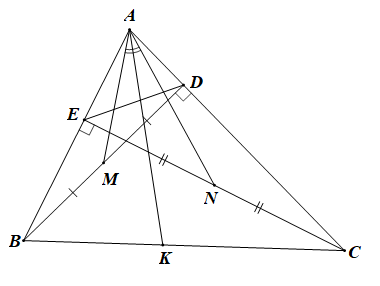
Xét và có
(chứng minh trên)
chung,
Do đó (c.g.c)
Suy ra (hai góc tương ứng)
Mặc khác (hai góc kề bù)
Do đó .
Vậy
Câu 17:
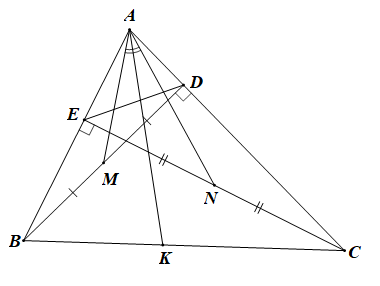
c) Gọi M, N lần lượt là trung điểm của đoạn thẳng BD và CE Vẽ AK là phân giác của Chứng minh KB.AC = KC.AB
 Xem đáp án
Xem đáp án
c) Vì (câu a) nên (tỉ số đồng dạng).
Mà M, N lần lượt là trung điểm của đoạn thẳng BD và CE nên và
Suy ra
Xét và có:
(chứng minh trên)
(do cùng phụ với )
Do đó (c.g.c).
Suy ra (hai góc tương ứng).
Lại có AK là tia phân giác của (giả thiết).
Suy ra (tính chất tia phân giác của một góc).
Do đó hay .
Nên AK là tia phân giác của .
Theo tính chất tia phân giác của tam giác ta có: .
Do đó (điều phải chứng minh).