Đề kiểm tra Cuối kì 2 Toán 8 CTST có đáp án (Đề 1)
-
428 lượt thi
-
18 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 2:
Cho hàm số Với giá trị nào của m thì hàm số đã cho là hàm số bậc nhất?
 Xem đáp án
Xem đáp án
Chọn đáp án D
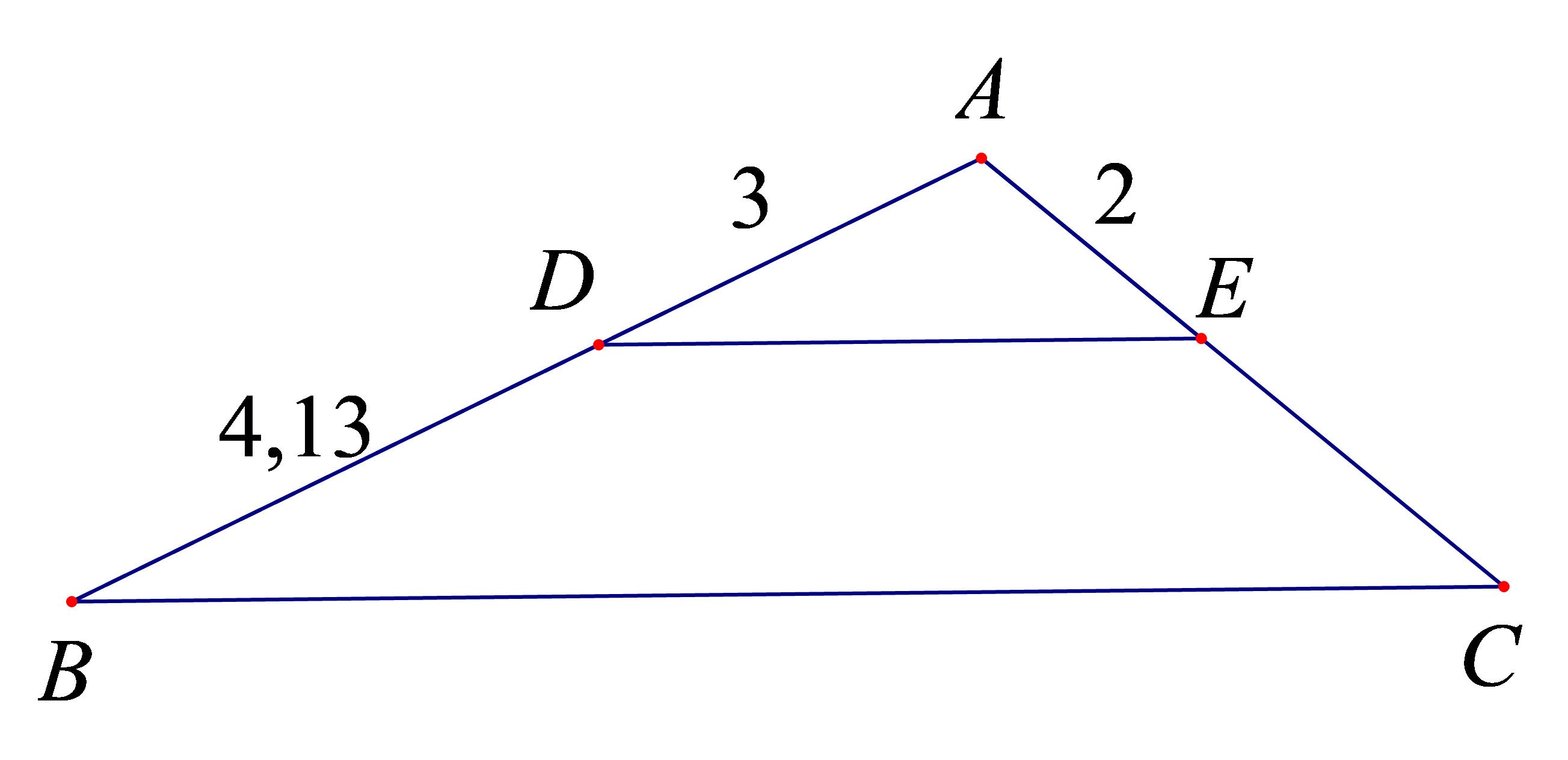
Câu 3:
Cho hàm số được xác định bởi công thức y = ax – 1. Biết đồ thị hàm số này đi qua điểm (1;2) Hoành độ của điểm thuộc đồ thị hàm số có tung độ bằng –4 là
 Xem đáp án
Xem đáp án
Chọn đáp án B
Câu 9:
 Xem đáp án
Xem đáp án
Chọn đáp án D
Câu 11:
Số kết quả có thể của hành động chọn ngẫu nhiên một chữ cái trong từ “MATHEMATIC” là
 Xem đáp án
Xem đáp án
Chọn đáp án B
Câu 12:
Bạn Nam tung một đồng xu cân đối và đồng chất 20 lần, có 13 lần mặt ngửa. Xác suất thực nghiệm của biến cố “Mặt sấp xuất hiện” là
 Xem đáp án
Xem đáp án
Chọn đáp án B
Câu 13:
Cho hàm số
a) Tính
b) Hoàn thành bảng sau:
| x
|
-2
|
? |
2 |
3 |
? |
| y = f(x)
|
? |
-4
|
? |
? |
8 |
 Xem đáp án
Xem đáp án
a) Thay lần lượt các giá trị x = -4; x = 8 vào f(x) , ta có:
b) Ta điền các số còn thiếu vào bảng như sau:
| x
|
-2
|
-1
|
2 |
3 |
|
| y = f(x)
|
-2
|
-4
|
2 |
|
8 |
Câu 14:
Đường sông từ A đến B ngắn hơn đường bộ là 10 km. Ca nô đi từ A đến B mất 2 giờ 20 phút, ô tô đi hết 2 giờ. Vận tốc ca nô nhỏ hơn vận tốc ô tô là 17 km/h
 Xem đáp án
Xem đáp án
Gọi x (km/h) là vận tốc của ca nô (x > 0).
Vận tốc của ô tô là: x + 17 (km/h).
Quãng đường ca nô đi là: .
Quãng đường ô tô đi là .
Vì đường sông ngắn hơn đường bộ 10 km nên ta có phương trình:
(thỏa mãn điều kiện).
Vậy vận tốc ca nô là 18 km/h. Vận tốc ô tô là 18 + 17 = 35 (km/h).Câu 15:
Viết ngẫu nhiên một số tự nhiên có hai chữ số nhỏ hơn 200.
a) Có bao nhiêu cách viết ngẫu nhiên một số tự nhiên như vậy?
b) Tính xác suất của mỗi biến cố “Số tự nhiên được viết ra là số tròn trăm”.
 Xem đáp án
Xem đáp án
a) Các số tự nhiên có hai chữ số nhỏ hơn 200 là: .
Vậy có 190 cách viết ngẫu nhiên một số tự nhiên có hai chữ số nhỏ hơn 200.
b) Có 9 kết quả thuận lợi cho biến cố“Số tự nhiên được viết ra là số tròn trăm” là
Do đó, xác suất của biến cố “Số tự nhiên được viết ra là số tròn trăm” là: .
Câu 16:
Để thiết kế mặt tiền cho căn nhà cấp bốn mái thái, sau khi xác định chiều dài mái PQ = 1,5 m. Chú thợ nhẩm tính chiều dài mái DE biết Q là trung điểm EC, P là trung điểm của DC. Tính giúp chú thợ xem chiều dài mái DE bằng bao nhiêu (xem hình vẽ minh họa)?
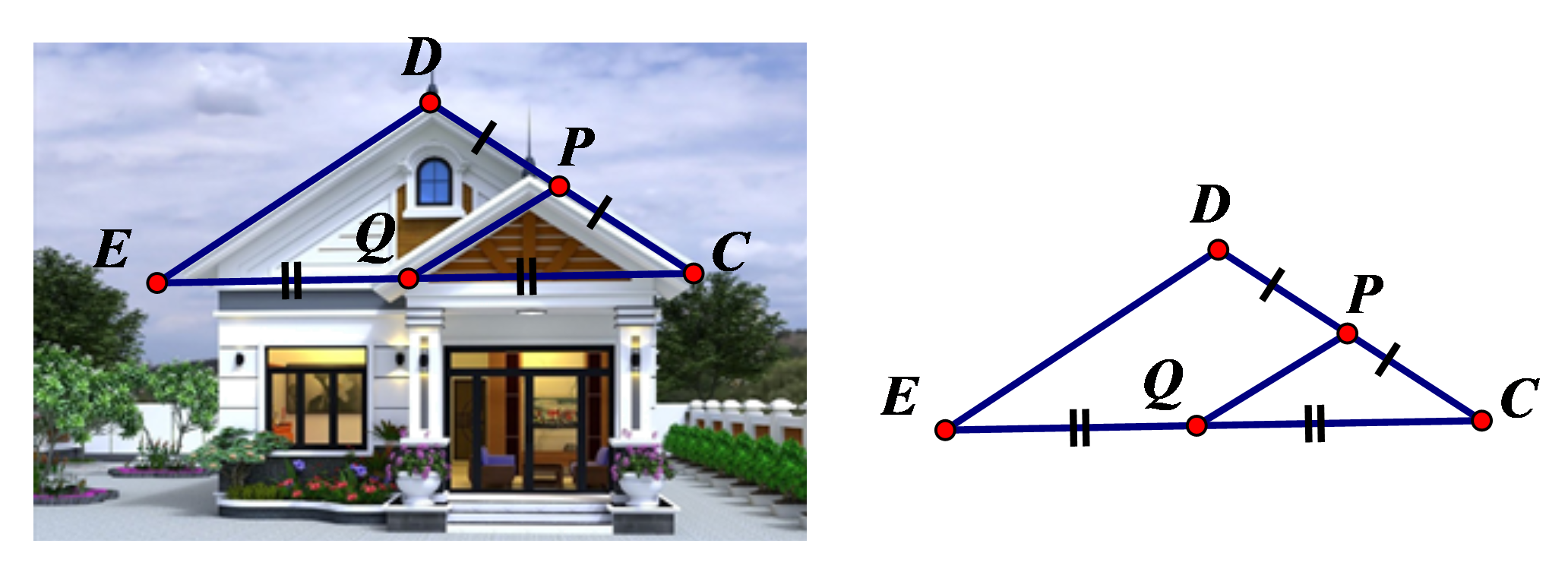
 Xem đáp án
Xem đáp án
Vì Q là trung điểm EC, P là trung điểm của DC nên PQ là đường trung bình của tam giác CED .
Khi đó .
Do đó .
Vậy chiều dài mái DE bằng 3 m.
Câu 17:
a) Chứng minh: .
b) Chứng minh: .
 Xem đáp án
Xem đáp án
a) Xét và có:
Do đó .
b) Xét và có:
Do đó
Suy ra hay (đpcm)
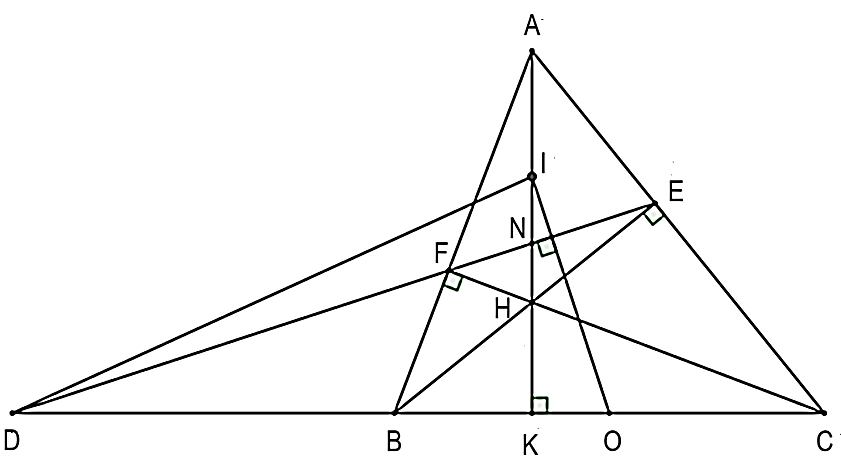
Câu 18:
c) Gọi N là giao điểm của AK và EF, D là giao điểm của đường thẳng BC và đường thẳng EF và O, I lần lượt là trung điểm của BC và AH. Chứng minh ON vuông góc DI.
 Xem đáp án
Xem đáp án
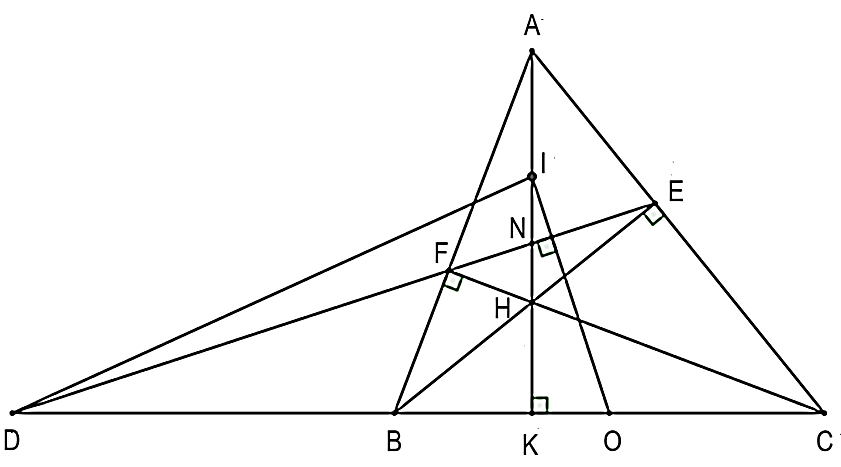
c)
• Xét vuông tại F có O là trung điểm của BC nên (1)
• Xét vuông tại E có O là trung điểm của BC nên (2)
Từ (1) và (2) nên suy ra (5)
• Xét vuông tại E có I là trung điểm của AH nên (3)
• Xét vuông tại F có I là trung điểm của AH nên (4)
Từ (3) và (4) nên suy ra (6)
Từ (5) và (6) ta suy ra được OI là đường trung trực của cạnh EF .
Khi đó hay .
Do đó DN là đường cao của .
Xét có DN và IK là đường cao và N là giao của DN và IK .
Do đó N là trực tâm của tam giác DOI .
Vậy (đpcm).