Đề kiểm tra 45 phút Toán 8 Chương 2 Hình Học có đáp án (Đề 1)
-
2952 lượt thi
-
8 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Phần trắc nghiệm (3 điểm)
Điền vào chỗ trống (…) để được khẳng định đúng. Đa giác có tất cả các cạnh bằng nhau và tất cả các góc là ………
Xem đáp án
Đa giác đều
Câu 4:
Khi chiều dài hình chữ nhật tăng lên 3 lần và chiều rộng không đổi thì diện tích hình chữ nhật về sau sẽ:
Xem đáp án
Chọn A
Câu 6:
Biết độ dài hai đường chéo của hình thoi là 4cm và 7cm. Diện tích hình thoi là:
Xem đáp án
Chọn B
Câu 7:
Phần tự luận (7 điểm)
a) Tính tổng các góc trong của đa giác 5 cạnh.
b) Cho ngũ giác đều ABCDE. Gọi F là giao điểm hai đường chéo AC và BE. Chứng minh tứ giác CFED là hình thoi.
Xem đáp án
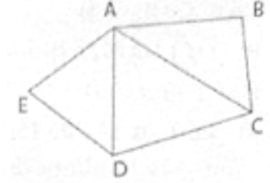
a) Nối AC; AD
Ngũ giác ABCDE được chia thành 3 tam giác: ΔABC, ΔACD, ΔADE. Tổng các góc trong của mỗi tam giác bằng 180o.
Tổng các góc trong của ngũ giác ABCDE là 180o.3 = 540o
b) Vì ABCDE là ngũ giác đều nên
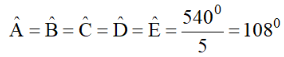
Mặt khác, ΔABC cân tại B nên:
Suy ra:
Lại có:
Suy ra ED // AC hay ED // CF.
Chứng minh tương tự ta có EF // CD
Mặt khác ED = DC (gt) nên tứ giác CEFD là hình thoi.
Câu 8:
Cho hình bình hành ABCD có diện tích S. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Đường thẳng BQ cắt AP tại E và cắt MC tại F. Đường thẳng DN cắt AP tại S và cắt MC tại R.
a) Chứng minh tứ giác EFRS là hình bình hành.
b) Tính diện tích hình bình hành EFRS theo S.
Xem đáp án
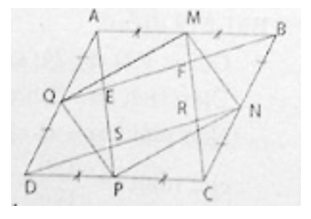
a) Ta có AB // CD (gt)
Suy ra AM // CP (1)
Lại có AM = AB/2; CP = CD/2 (2)
Từ (1) và (2) suy ra AMCP là hình bình hành
Suy ra AP // CM hay ES // FR.
Tương tự ta cũng chứng minh được tứ giác BQDN là hình bình hành nên BQ // DN. Suy ra EF // RS.
Vậy tứ giác EFRS là hình bình hành
b) Đặt PS = x. Suy ra CR = 2x (tính chất đường trung bình)
Từ đó suy ra RF = ES = AE = 2x
Suy ra: ES = 2AP/5 => SEFRS = 2SAMCP/5
Vì SAMCP = SABCD/2 nên SEFRS = SABCD/2