10 câu hỏi trắc nghiệm thuộc Dạng 4: Bài toán thực tiễn gắn với việc vận dụng định lí Thalès có đáp án

Trắc nghiệm Toán 8 Bài 15. Định lí Thalès trong tam giác có đáp án

Dạng 4: Bài toán thực tiễn gắn với việc vận dụng định lí Thalès có đáp án

702 lượt thi
10 câu hỏi
60 phút

Danh sách câu hỏi

Câu 1:

Bóng (AK) của một cột điện (MK) trên mặt đất dài 6 m. Cùng lúc đó một cột đèn giao thông (DE) cao 3 m có bóng (AE) dài 2 m. Chiều cao của cột điện (MK) là

A. 8 m;

B. 9 m;

C. 1 m;

D. 4 m.

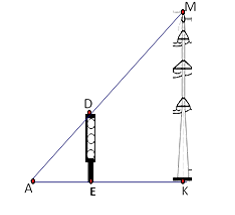
Xem đáp án

Đáp án đúng là: B

Xét tam giác AMK có DE // MK (cùng vuông góc với AK) nên theo hệ quả của định lí Thalès, ta có:

$\frac{AE}{AK} = \frac{DE}{MK}$ hay $\frac{2}{6} = \frac{3}{MK}$ .

Suy ra $MK = \frac{6 \cdot 3}{2} = 9$ (m).

Câu 2:

Để đo chiều cao AC của một cột cờ, người ta cắm một cái cọc ED có chiều cao 2 m vuông góc với mặt đất. Đặt vị trí quan sát tại B, biết khoảng cách BE là 1,5 m và khoảng cách AB là 9 m. Chiều cao AC của cột cờ là:

A. 3 m;

B. 6,75 m;

C. 12 m;

D. 9 m.

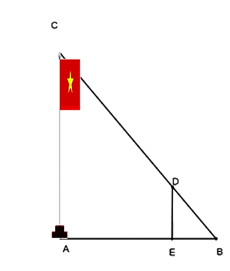
Xem đáp án

Đáp án đúng là: C

Xét tam giác ABC có DE // AC (cùng vuông góc với AB) nên theo hệ quả của định lí Thalès, ta có:

$\frac{DE}{AC} = \frac{BE}{AB}$ hay $\frac{2}{AC} = \frac{1, 5}{9}$ .

Suy ra $AC = \frac{2 \cdot 9}{1, 5} = 12$ (m).

Câu 3:

Cho hình vẽ dưới đây, biết cái cây có chiều cao ED = 2 m và khoảng cách AE = 4 m, EC = 2,5 m. Khi đó chiều cao AB của ngôi nhà là:

A. AB = 5,2 m;

B. AB = 3,2 m;

C. AB = 1,25 m;

D. AB = 3,5 m.

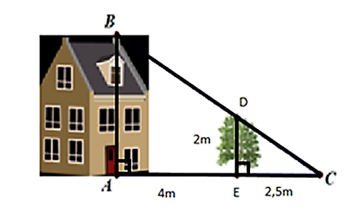
Xem đáp án

Đáp án đúng là: A

Ta có CA = CE + AE = 2,5 + 4 = 6,5 (m).

Xét tam giác ABC có DE // AB (cùng vuông góc với AC) nên theo hệ quả của định lí Thalès, ta có:

$\frac{DE}{AB} = \frac{CE}{CA}$ hay $\frac{2}{AB} = \frac{2, 5}{6, 5}$ .

Suy ra $AB = \frac{2 \cdot 6, 5}{2, 5} = 5, 2$ (m).

Câu 4:

Một cột đèn cao 15 m chiếu sáng một cây xanh như hình bên dưới. Cây cách cột đèn 3 m và có bóng trải dài dưới mặt đất là 5 m. Tìm chiều cao của cây xanh.

A. 5,793 m;

B. 5,397 m;

C. 9,573 m;

D. 9,375 m.

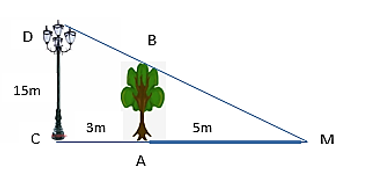
Xem đáp án

Đáp án đúng là: D

Ta có CM = MA + AC = 3 + 5 = 8 (m).

Xét tam giác CMD có AB // CD (cùng vuông góc với CM) nên theo hệ quả của định lí Thalès, ta có:

$\frac{MA}{MC} = \frac{BA}{DC}$ hay $\frac{5}{8} = \frac{BA}{15}$ .

Suy ra $BA = \frac{5 \cdot 15}{8} = 9, 375$ (m).

Câu 5:

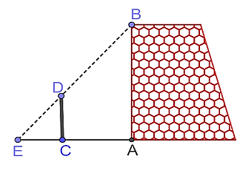
Một nhóm các bạn học sinh lớp 8 đã thực hành đo chiều cao AB của một bức tường như sau: Dùng một cái cọc CD đặt cố định vuông góc với mặt đất, với CD = 3 m và CA = 5 m. Sau đó, các bạn đã phối hợp để tìm được điểm E trên mặt đất là giao điểm của hai tia BD, AC và đo được CE = 2 m (Hình vẽ bên). Chiều cao AB của bức tường là:

A. 7,5 m;

B. 1,2 m;

C. 3,3 m;

D. 10,5 m.

Xem đáp án

Đáp án đúng là: D

Có AE = EC + CA = 2 + 5 = 7 (m).

Xét tam giác EAB có DC // AB (cùng vuông góc với AE) nên theo hệ quả của định lí Thalès, ta có:

$\frac{EC}{EA} = \frac{DC}{AB}$ hay $\frac{2}{7} = \frac{3}{AB}$ .

Suy ra $\frac{2}{7} = \frac{3}{AB}$ (m).

Câu 6:

Để đo khoảng cách giữa hai điểm A và B (không thể đo trực tiếp). Người ta xác định các điểm C, D, E như hình vẽ. Sau đó đo được khoảng cách giữa A và C là AC = 4 m, khoảng cách giữa C và E là EC = 1 m; khoảng cách giữa E và D là DE = 3 m. Tính khoảng cách giữa hai điểm A và B.

A. 21 m;

B. 11 m;

C. 12 m;

D. 22 m.

Xem đáp án

Đáp án đúng là: C

Xét tam giác ABC có DE // AD (cùng vuông góc với AC) nên theo định lí Thalès, ta có:

$\frac{EC}{AC} = \frac{ED}{AB}$ hay $\frac{1}{4} = \frac{3}{AB}$ .

Suy ra $AB = \frac{3 \cdot 4}{1} = 12$ (m).

Câu 7:

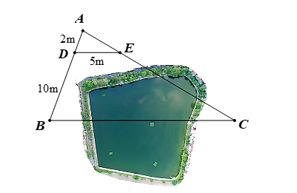
Giữa hai điểm B và C có một cái ao. Để đo khoảng cách BC người ta đo được các đoạn thẳng AD = 2 m, BD = 10 m và DE = 5 m. Biết DE // BC, tính khoảng cách giữa hai điểm B và C.

A. 30 m;

B. 25 m;

C. 20 m;

D. 15 m.

Xem đáp án

Đáp án đúng là: A

Có AB = AD + DB = 2 + 10 = 12 (m).

Xét tam giác ABC có DE // BC nên theo hệ quả của định lí Thalès, ta có:

$\frac{AD}{AB} = \frac{DE}{BC}$ hay $\frac{2}{12} = \frac{5}{BC}$

Suy ra $BC = \frac{5 \cdot 12}{2} = 30$ (m).

Câu 8:

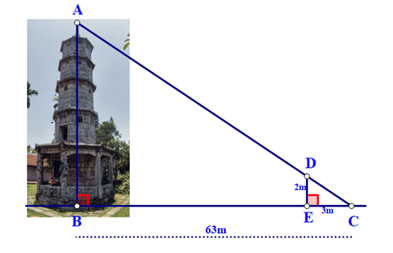
Bóng của một tháp trên mặt đất có độ dài BC = 63 m. Cùng thời điểm đó, một cây cột DE cao 2 m cắm vuông góc với mặt đất có bóng dài 3 m. Chiều cao của tháp là:

A. 24 m;

B. 42 m;

C. 44 m;

D. 22 m.

Xem đáp án

Đáp án đúng là: B

Xét tam giác ABC có DE // AB (cùng vuông góc với BC) nên theo hệ quả của định lí Thalès, ta có:

$\frac{CE}{BC} = \frac{DE}{AB}$ hay $\frac{3}{63} = \frac{2}{AB}$ .

Suy ra $AB = \frac{63 \cdot 2}{3} = 42$ (m).

Câu 9:

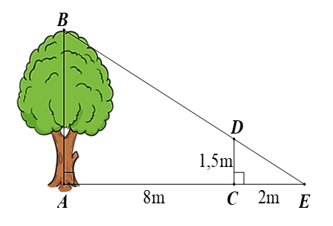
Một người cắm một cái cọc vuông góc với mặt đất sao cho bóng của đỉnh cọc trùng với bóng của ngọn cây. Biết cọc cao 1,5 m so với mặt đất, chân cọc cách gốc cây 8 m và cách bóng của đỉnh cọc 2 m. Tính chiều cao của cây.

A. 7,5 m;

B. 6 m;

C. 5,5 m;

D. 7 m.

Xem đáp án

Đáp án đúng là: A

Có AE = AC + CE = 8 + 2 = 10 (m).

Xét tam giác ABE có DC // AB (cùng vuông góc với AE) nên theo hệ quả của định lí Thalès, ta có:

$\frac{CE}{AE} = \frac{DC}{AB}$ hay $\frac{2}{10} = \frac{1,5}{AB}$ .

Suy ra $AB = \frac{10 \cdot 1, 5}{2} = 7, 5$ (m).

Câu 10:

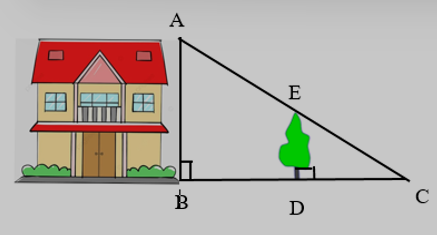
Để tính chiều cao AB của một ngôi nhà (như hình vẽ), người ta đo chiều cao của cái cây ED = 4 m và biết được các khoảng cách BD = 7 m, DC = 5 m. Khi đó chiều cao AB của ngôi nhà là:

A. 5,6 m;

B. 6,9 m;

C. 9,6 m;

D. 4,36 m.

Xem đáp án

Đáp án đúng là: C

Có BC = BD + DC = 7 + 5 = 12 (m).

Xét tam giác ABC có ED // AB (cùng vuông góc với BC) nên theo hệ quả của định lí Thalès, ta có:

$\frac{DE}{AB} = \frac{CD}{CB}$ hay $\frac{4}{AB} = \frac{5}{12}$

Suy ra $AB = \frac{4 \cdot 12}{5} = 9, 6$ (m).

Bắt đầu thi ngay