10 câu hỏi trắc nghiệm thuộc Dạng 2: Bài toán thực tiễn có vận dụng tính chất đường phân giác của tam giác có đáp án

Câu 1:

Hình dưới đây minh họa một phần nền nhà được lát bởi các viên gạch hình vuông khít nhau trong đó các điểm A, B, C, D là bốn đỉnh của một viên gạch. Đặt một thước gỗ trên mặt nền nhà sao cho thước gỗ luôn đi qua điểm C và cắt tia AB tại M, cắt tia AD tại N. Khẳng định nào sau đây sai?

A. $\frac{C M}{C N} = \frac{A M}{A N};$

B. $\frac{C N}{A N} = \frac{C M}{A M};$

C. $\frac{A N}{C N} = \frac{A M}{C M};$

D. $\frac{C N}{A M} = \frac{C M}{A N} .$

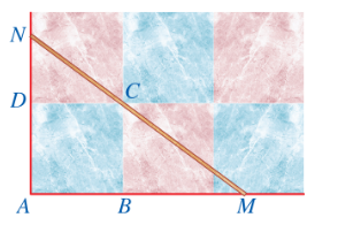
Xem đáp án

Đáp án đúng là: D

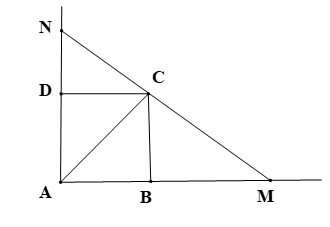
Ta có: ABCD là hình vuông và AC là đường chéo nên AC là đường phân giác của $\hat{D A B}$ hay AC là đường phân giác của $\hat{N A M} .$

Áp dụng tính chất đường phân giác trong với AC là đường phân giác của $\hat{N A M}$ ta có: $\frac{C N}{C M} = \frac{A N}{A M} \Rightarrow \frac{C N}{A N} = \frac{C M}{A M}; \frac{A N}{C N} = \frac{A M}{C M} .$

Như vậy, phương án A, B, C mang nội dung đúng; phương án D mang nội dung sai.

Câu 2:

Một người đứng đỉnh tháp Busan (điểm D) quan sát ba điểm thẳng hàng A, B, C lần lượt là chân ba cột đèn sao cho A, B, C thẳng hàng (như hình dưới đây). Người đó nhận thấy góc nhìn đến hai điểm A, B thì bằng góc nhìn đến hai điểm B, C, tức là $\hat{A D B} = \hat{B D C} .$ Hỏi tỉ số khoảng cách từ vị trí D đang đứng đến điểm A và đến điểm C mà không cần phải đo trực tiếp hai khoảng cách đó bằng bao nhiêu? Biết khoảng cách giữa hai chân cột đèn A, B là 30 m và khoảng cách giữa hai chân cột đèn B, C là 25 m.

A. $\frac{6}{5};$

B. $\frac{5}{6};$

C. $\frac{1}{3};$

D. 1

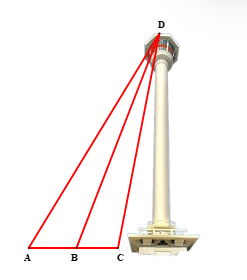
Xem đáp án

Đáp án đúng là: A

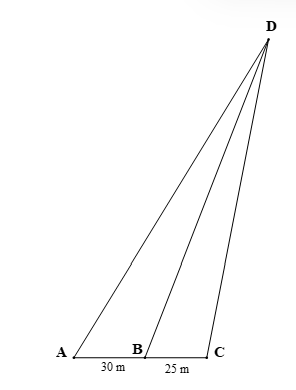
Từ giả thiết ta có: AB = 30 m, BC = 25m;

$\hat{A D B} = \hat{B D C}$ suy ra DB là tia phân giác $\hat{A D C} .$

Xét ∆ADC có DB là tia phân giác $\hat{A D C},$ nên áp dụng tính chất đường phân giác trong

∆ADC ta có: $\frac{D A}{D C} = \frac{B A}{B C} = \frac{30}{25} = \frac{6}{5} .$

Vậy tỉ số khoảng cách từ vị trí D đang đứng đến điểm A và đến điểm C bằng $\frac{6}{5} .$

Câu 3:

Hai ngư dân A, B đứng ở hai bên bờ sông cách một cái lều M lần lượt là 14 m; 20 m và cùng nhìn thấy một cù lao C trên sông (được mô tả như hình vẽ) sao cho $\hat{A C M} = \hat{M C B} .$ Hỏi tỉ số khoảng cách của ngư dân A và B đến cù lao C trên sông là bao nhiêu?

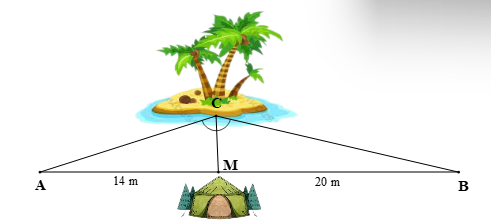
Hai ngư dân A, B đứng ở hai bên bờ sông cách một cái lều M lần lượt là 14 m; 20 m và cùng nhìn thấy một cù lao C trên sông (được mô tả như hình vẽ) sao cho (ảnh 1)

A. $\frac{7}{10};$

B. $\frac{17}{10};$

C. $\frac{10}{7};$

D. $\frac{17}{3} .$

Xem đáp án

Đáp án đúng là: A

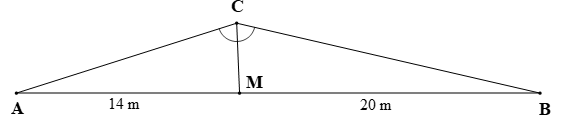
Hai ngư dân A, B đứng ở hai bên bờ sông cách một cái lều M lần lượt là 14 m; 20 m và cùng nhìn thấy một cù lao C trên sông (được mô tả như hình vẽ) sao cho (ảnh 2)

Từ giả thiết ta có: MA = 14 m, MB = 20 m;

$\hat{A C M} = \hat{M C B}$ suy ra CM là tia phân giác $\hat{A C B} .$

Xét ∆ACB có CM là tia phân giác $\hat{A C B},$ nên áp dụng tính chất đường phân giác trong

∆ACB ta có: $\frac{C A}{C B} = \frac{M A}{M B} = \frac{14}{20} = \frac{7}{10} .$

Vậy tỉ số khoảng cách của ngư dân A và B đến cù lao C trên sông là $\frac{7}{10} .$

Câu 4:

Ba bạn Mai, Lan, Điệp hẹn gặp nhau tại nhà bạn Lan, biết rằng nhà bạn Mai ở vị trí A, nhà bạn Lan ở vị trí G và nhà bạn Điệp ở vị trí M (được mô tả như hình vẽ). Biết rằng tứ giác ABCD là hình vuông và M là trung điểm của CD. Quãng đường bạn Điệp đi từ nhà tới nhà bạn Lan là 3 km. Hỏi bạn Mai phải đi quãng đường ngắn nhất từ nhà tới nhà bạn Lan là bao nhiêu kilômét để gặp Lan và Điệp?

A. 12 km;

B. 2 km;

C. 3 km;

D. 6 km.

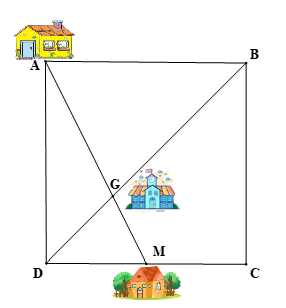
Xem đáp án

Đáp án đúng là: D

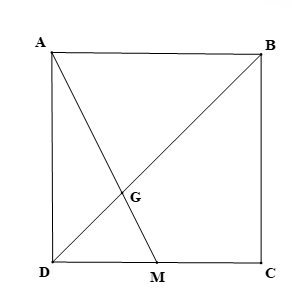
Theo bài ra ta có: GM = 3 km.

Vì ABCD là hình vuông nên CD = AD và DB là tia phân giác của $\hat{A D C} .$

Do M là trung điểm của DC nên $D M = \frac{1}{2} D C = \frac{1}{2} D A$ (do CD = AD).

$\Rightarrow \frac{D M}{D A} = \frac{1}{2} .$

Xét ∆ADM có: DG là tia phân giác của $\hat{A D M}$ (do DB là tia phân giác của $\hat{A D C}$ ).

Áp dụng tính chất đường phân giác trong ∆ADM với DG là tia phân giác của $\hat{A D M}$ ta có:

$\frac{D M}{D A} = \frac{G M}{G A} \Rightarrow \frac{1}{2} = \frac{3}{G A} \Rightarrow G A = 6$ (km).

Vậy bạn Mai phải đi quãng đường ngắn nhất từ nhà tới nhà bạn Lan là GA = 6 km để gặp Lan và Điệp.

Câu 5:

Để bảo trì tượng nữ thần tự do với chiều cao là AD = 93 m người thợ đã gắn hai dây thép cố định vào hai vị trí B và C (như hình vẽ) sao cho $\hat{B A C} = \hat{C A D} .$ Tính chiều dài của dây thép khi được căng thẳng từ A đến B biết rằng độ dài BC = 20 m và CD = 15 m

Để bảo trì tượng nữ thần tự do với chiều cao là AD = 93 m người thợ đã gắn hai dây thép cố định vào hai vị trí B và C (như hình vẽ) sao cho (ảnh 1)

A. 125 m;

B. 124 m;

C. 100 m;

D. 69,75 m.

Xem đáp án

Đáp án đúng là: B

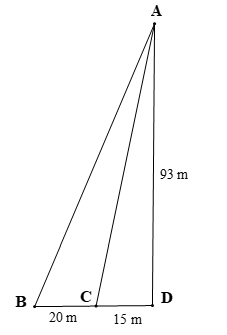
Để bảo trì tượng nữ thần tự do với chiều cao là AD = 93 m người thợ đã gắn hai dây thép cố định vào hai vị trí B và C (như hình vẽ) sao cho (ảnh 2)

Do $\hat{B A C} = \hat{C A D}$ nên AC là đường phân giác của $\hat{B A D} .$

Xét ∆BAD có AC là đường phân giác của $\hat{B A D},$ nên áp dụng tính chất đường phân giác trong ∆BAD ta có:

$\frac{C B}{C D} = \frac{A B}{A D} \Rightarrow \frac{20}{15} = \frac{A B}{93}$ ⇒ AB ∙ 15 = 20 ∙ 93 ⇒ AB ∙ 15 = 1 860

$\Rightarrow A B = \frac{1 860}{15} = 124$ (m).

Vậy chiều dài của dây thép khi được căng thẳng từ A đến B là 124 m.

Câu 6:

Lúc 6 giờ sáng, bạn Hải đi xe đạp (điểm A) đến trường B phải leo lên và xuống một con dốc với đỉnh dốc tại điểm C (như hình vẽ). Điểm H là một điểm thuộc đoạn thẳng AB sao cho CH đường là phân giác $\hat{A C B},$ AH = 0,32 km và BH = 0,4 km. Biết bạn Hải đi xe đạp đến C lúc 6 giờ 30 phút với tốc độ trung bình lên dốc là 4 km/h. Hỏi bạn Hải đến trường lúc mấy giờ nếu tốc độ trung bình xuống dốc là 10 km/h.

A. 6 giờ 45 phút;

B. 7 giờ;

C. 7 giờ 15 phút;

D. 7 giờ 30 phút.

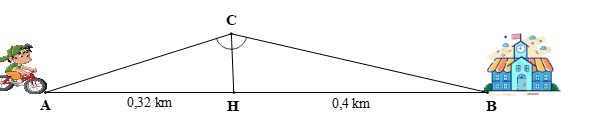
Xem đáp án

Đáp án đúng là: A

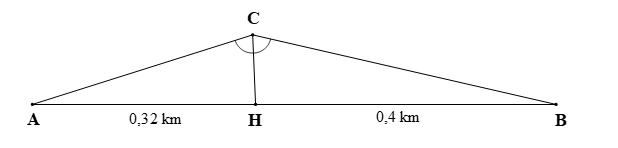
Thời gian để bạn Hải đi từ A đến C là: 6 giờ 30 phút – 6 giờ = 30 phút = 0,5 giờ.

Quãng đường mà bạn Hải đi từ A đến C trong 0,5 giờ với tốc độ trung bình lên dốc 4 km/h là: AC = S_A→C = 4 ∙ 0,5 = 2 (km).

Xét ∆ACB có CH là đường phân giác của $\hat{A C B},$ nên áp dụng tính chất đường phân giác trong ∆ACB ta có:

$\frac{H A}{H B} = \frac{C A}{C B} \Rightarrow \frac{0, 32}{0, 4} = \frac{2}{C B}$ ⇒ 0,32 ∙ CB = 0,4 ∙ 2 ⇒ 0,32 ∙ CB = 0,8

$\Rightarrow C B = \frac{0, 8}{0, 32} = 2, 5$ (m).

Thời gian để bạn Hải đi hết quãng đường CB = 2,5 m với tốc độ trung bình xuống dốc 10 km/h là: $\frac{2, 5}{10} = 0, 25$ (giờ).

Như vậy, tổng thời gian bạn Hải đi từ A đến trường B là

0,5 + 0,25 = 0,75 (giờ) = 45 (phút).

Do đó bạn Hải đến trường lúc 6 giờ 45 phút.

Câu 7:

Nhà bạn Bảo ở vị trí M, nhà bạn Lan ở vị trí D (như hình bên dưới), biết rằng tứ giác ABCD là hình thoi và AB = 3AM. Hai bạn đi bộ với cùng một vận tốc trên con đường MD để đi đến điểm I. Bạn Lan xuất phát lúc 7 giờ. Hỏi bạn Bảo phải xuất phát lúc mấy giờ để gặp bạn Lan lúc 7 giờ 30 phút tại điểm I?

A. 7 giờ;

B. 7 giờ 15 phút;

C. 7 giờ 20 phút;

D. 7 giờ 30 phút.

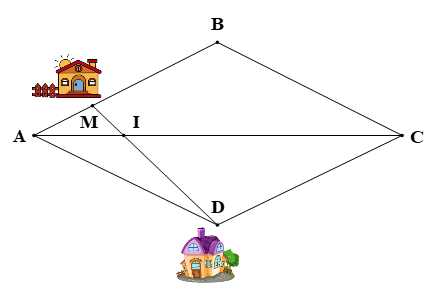
Xem đáp án

Đáp án đúng là: C

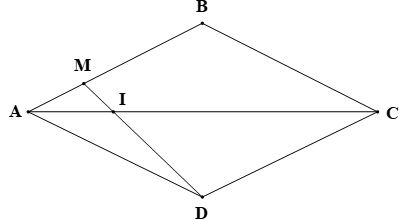
Theo đề bài, ABCD là hình thoi nên AB = AD và AC là tia phân giác của $\hat{B A D} .$

Ta có: AB = 3AM hay AD = 3AM (do AB = AD).

$\Rightarrow \frac{A M}{A D} = \frac{1}{3} .$

Xét ∆MAD có: AI là tia phân giác của $\hat{M A D}$ (do AC là tia phân giác của $\hat{B A D}$ ),

Áp dụng tính chất đường phân giác trong ∆MAD ta có:

$\frac{A M}{A D} = \frac{I M}{I D} \Rightarrow \frac{1}{3} = \frac{I M}{I D} \Rightarrow I M = \frac{1}{3} I D .$

Theo đề bài, I là địa điểm gặp nhau nên bạn Bảo đi theo quãng đường MI, bạn Lan đi theo quãng đường DI.

Ta có: S = vt, mà quãng đường bạn Bảo đi bằng $\frac{1}{3}$ lần quãng đường bạn Lan đi và vận tốc đi bộ của hai bạn đều bằng nhau nên thời gian bạn Bảo đi bằng $\frac{1}{3}$ lần thời gian bạn Lan đi thì hai bạn mới gặp nhau tại địa điểm I.

Bạn Bảo gặp bạn Lan lúc 7 giờ 30 phút nên thời gian bạn Lan đi hết quãng đường MI là:

7 giờ 30 phút – 7 giờ = 30 phút.

Khi đó, thời gian bạn Bảo đi là $\frac{1}{3} \cdot 30 = 10$ (phút).

Do đó, bạn Bảo phải xuất phát từ lúc: 7 giờ 30 phút – 10 phút = 7 giờ 20 phút.

Vậy bạn Bảo phải xuất phát lúc 7 giờ 20 phút để gặp bạn Lan lúc 7 giờ 30 phút tại điểm I.

Câu 8:

Một chiếc thuyền xuất phát từ vị trí I chở hàng cho hai hòn đảo A và B theo phương thẳng (được minh họa như trong hình vẽ). Một người đứng ở vị trí K trên bờ quan sát ba điểm thẳng hàng I, A, B. Người đó nhận thấy góc nhìn đến hai điểm I, A thì bằng góc nhìn đến hai điểm A, B, tức là

\hat{I K A} = \hat{A K B} .

Biết rằng thuyền đi từ vị trí I đến hòn đảo A là 500 m; từ hòn đảo A đến hòn đảo B là 6 km và khoảng cách từ người đó đến vị trí I là 1 km. Tính khoảng cách từ người đó (vị trí K) đến hòn đảo B?

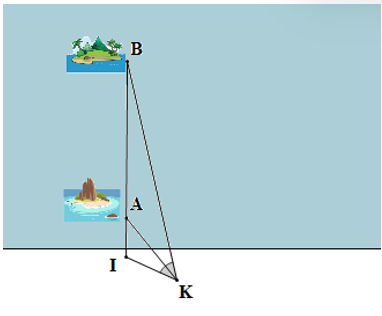
Một chiếc thuyền xuất phát từ vị trí I chở hàng cho hai hòn đảo A và B theo phương thẳng (được minh họa như trong hình vẽ). Một người đứng ở vị trí K trên bờ quan sát ba điểm thẳng hàng I, A, B. Người đó nhận thấy góc nhìn đến hai điểm I, A thì bằng góc nhìn đến hai điể (ảnh 1)

A. 10 km;

B. 20 km;

C. 15 km;

D. 12 km.

Xem đáp án

Đáp án đúng là: D

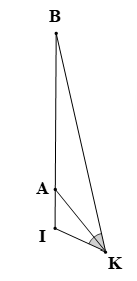
Theo bài ra ta có: IA = 500 m = 0,5 km, AB = 6 km, IK = 1 km.

Vì $\hat{I K A} = \hat{A K B}$ nên AK là đường phân giác của $\hat{I K B} .$

Áp dụng tính chất đường phân giác trong ∆IKB có:

$\frac{A B}{A I} = \frac{B K}{I K} \Rightarrow \frac{6}{0, 5} = \frac{B K}{1} \Rightarrow B K = \frac{6}{0, 5} = 12$ (km).

Vậy khoảng cách từ người đó (vị trí K) đến hòn đảo B là BK = 12 km.

Câu 9:

Hai vận động viên thi chạy Marathon xuất phát tại điểm A cùng một thời điểm, chạy theo hai hướng khác nhau đến B và C. Sau t phút hai người đó gặp nhau tại D (được mô tả như hình vẽ). Cho độ dài AB = 3 km; AC = 3,5 km; BC = 5 km và $\hat{B A D} = \hat{C A D} .$ Hỏi trong t phút đầu tiên vận động viên nào chạy nhanh hơn?

A. Vận động viên chạy từ A qua B trước rồi đến D chạy nhanh hơn vận động viên chạy từ A qua C trước rồi đến D.

B. Vận động viên chạy từ A qua C trước rồi đến D chạy nhanh hơn vận động viên chạy từ A qua B trước rồi đến D.

C. Hai vận động viên chạy với cùng một tốc độ trung bình.

D. Không thể kết luận vận động viên nào chạy nhanh hơn.

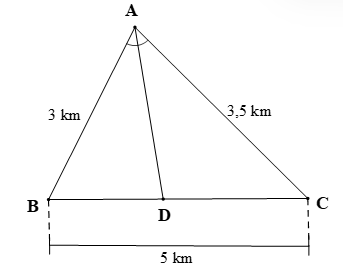
Xem đáp án

Đáp án đúng là: B

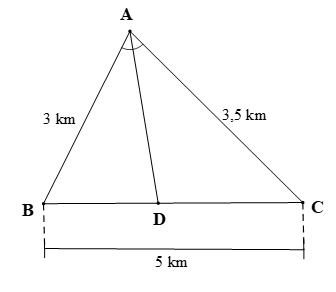
Vì $\hat{B A D} = \hat{C A D}$ nên AD là đường phân giác của $\hat{B A C} .$

Áp dụng tính chất đường phân giác trong ∆BAC có: $\frac{D B}{D C} = \frac{A B}{A C}$ .

Suy ra $\frac{D B}{A B} = \frac{D C}{A C} = \frac{D B + D C}{A B + A C} = \frac{B C}{A B + A C} \Rightarrow \frac{D B}{3} = \frac{D C}{3, 5} = \frac{5}{3 + 3, 5} = \frac{10}{13}$

$\Rightarrow \frac{D B}{3} = \frac{10}{13} \Rightarrow D B = \frac{3 \cdot 10}{13} = \frac{30}{13} \approx 2, 31$ (km);

Và $\frac{D C}{3, 5} = \frac{10}{13} \Rightarrow D C = \frac{3, 5 \cdot 10}{13} = \frac{35}{13} \approx 2, 69$ (km).

Quãng đường vận động viên chạy từ A qua B trước rồi đến D là:

AB + DB ≈ 3 + 2,31 = 5,31 (km).

Quãng đường vận động viên chạy từ A qua C trước rồi đến D là:

AC + DC ≈ 3,5 + 2,69 = 6,19 (km).

Biết hai vận động viên xuất phát cùng một thời điểm và sau t phút thì hai vận động viên gặp nhau tại D nên thời gian chạy của hai vận động viên là như nhau. Mà quãng đường vận động viên chạy từ A qua B trước rồi đến D nhỏ hơn quãng đường vận động viên chạy từ A qua C trước rồi đến D (do 5,31 km < 6,19 km).

Do đó, trong t phút đầu vận động viên chạy từ A qua C trước rồi đến D sẽ chạy nhanh hơn vận động viên chạy từ A qua B trước rồi đến D.

Câu 10:

Nhà bạn Hoa ở vị trí K, nhà bạn Phương ở vị trí A (như hình bên dưới), biết rằng tứ giác ABCD là hình thoi và K là trung điểm của BC. Hai bạn đi xe đạp với cùng một vận tốc trên con đường AK để đi đến điểm H. Bạn Hoa xuất phát lúc 8 giờ. Hỏi bạn Phương phải xuất phát lúc mấy giờ để gặp bạn Hoa lúc 8 giờ 15 phút tại điểm H?

A. 7 giờ 45 phút;

B. 7 giờ 30 phút;

C. 7 giờ 20 phút;

D. 7 giờ.

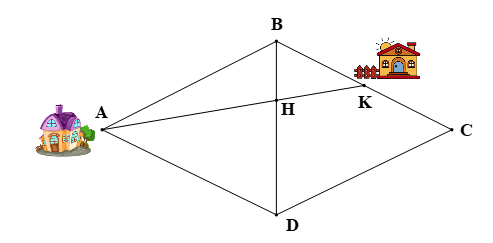
Xem đáp án

Đáp án đúng là: A

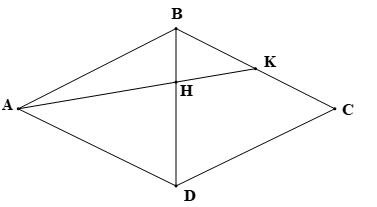
Theo đề bài, ABCD là hình thoi nên BA = BC và BD là tia phân giác của $\hat{A B C} .$

Vì K là trung điểm của BC nên $B K = \frac{1}{2} B C = \frac{1}{2} B A \Rightarrow \frac{B K}{B A} = \frac{1}{2} .$

Xét ∆ABK có: BH là tia phân giác của $\hat{A B K}$ (do BD là tia phân giác của $\hat{A B C}$ ).

Áp dụng tính chất đường phân giác trong ∆ABK với BH là tia phân giác của $\hat{A B K}$ ta có:

$\frac{B K}{B A} = \frac{H K}{H A} \Rightarrow \frac{1}{2} = \frac{H K}{H A} \Rightarrow H A = 2 H K .$

Theo đề bài, H là địa điểm gặp nhau nên bạn Hoa đi theo quãng đường KH, bạn Phương đi theo quãng đường AH.

Ta có: S = vt, mà quãng đường bạn Phương đi bằng 2 lần quãng đường bạn Hoa đi và vận tốc đi xe đạp của hai bạn đều bằng nhau nên thời gian bạn Phương đi bằng 2 lần thời gian bạn Hoa đi thì hai bạn mới gặp nhau tại địa điểm H.

Bạn Phương gặp bạn Hoa lúc 8 giờ 15 phút và Hoa xuất phát lúc 8 giờ nên thời gian bạn Hoa đi hết quãng đường KH là:

8 giờ 15 phút – 8 giờ = 15 phút.

Khi đó, thời gian bạn Phương đi là 2 ∙ 15 = 30 (phút).

Do đó, bạn Phương phải xuất phát từ lúc: 8 giờ 15 phút – 30 phút = 7 giờ 45 phút.

Vậy bạn Phương phải xuất phát lúc 7 giờ 45 phút giờ để gặp bạn Hoa lúc 8 giờ 15 phút tại điểm H.