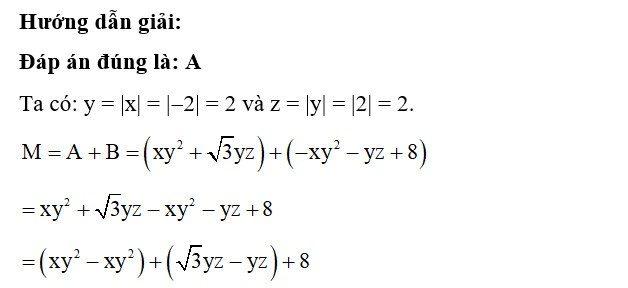10 câu hỏi trắc nghiệm thuộc Dạng 2: Tính giá trị của đa thức

Câu 1:

Giá trị của tổng hai đa thức A = -3x²y² và B = x³ + 3y tại $x = \frac{1}{2}; y = 1$ là

A. $\frac{5}{2}$ ;

B. $\frac{19}{8}$ ;

C. 1;

D. $\frac{‐ 3}{4}$ .

Xem đáp án

Câu 2:

Cho đa thức M = 19xy – 7x³y + 9x²; N = 10xy – 2x³ – 9x² và P = 12x³y – 4x². Giá trị của đa thức Q = M – N + P tại x = 1 và y = –2 là

A. 2;

B. –30;

C. 26;

D. –66.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B

Ta có Q = M – N + P

= (19xy – 7x³y + 9x²) – (10xy – 2x³ – 9x²) + (12x³y – 4x²)

= 19xy – 7x³y + 9x² – 10xy + 2x³ + 9x² + 12x³y – 4x²

= (19xy – 10xy) + (–7x³y + 12x³y) + (9x² + 9x² – 4x²) + 2x³

= 9xy + 5x³y – 4x² + 2x³.

Thay x = 1 và y = –2 vào biểu thức Q đã thu gọn ở trên ta được:

Q = 9.1.(–2) + 5.1³.(–2) – 4.1² + 2.1³

= –18 – 10 – 4 + 2

= –30.

Câu 3:

Cho hai đa thức A = xy² + x² - 1,2y² và B = ax² + 1, với a là hằng số. Giá trị của M = 2A - 3B tại x = 1; y = |–2| là 0,4. Giá trị của a là

A. 1;

B. -1;

C.

\frac{22}{3}

;

D. 2.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B

Ta có: y = |–2| = 2.

M = 2A - 3B

= 2(xy² + x² - 1,2y²) - 3(ax² + 1)

= 2xy² + 2x² - 2,4y² - 3ax² - 3

= 2xy² + (2x²- 3ax²) - 2,4y²- 3

= 2xy² + (2 - 3a)x² - 2,4y²- 3

Thay x = 1; y = 2 vào đa thức M đã thu gọn, ta được:

M = 2.1.2² + (2 - 3a).1² - 2,4.2²- 3

= 8 + 2 - 3a - 9,6 - 3

= -3a - 2,6.

Theo bài, với x = 1; y = 2 thì M = 0,4 nên -3a - 2,6 = 0,4.

Suy ra 3a = -2,6 - 0,4 = -3

Do đó a = -1.

Câu 4:

An và Bình cùng đạp xe tiếp sức. Sau khi An đạp được x giờ với vận tốc 12 km/h thì Bình đạp nối tiếp với vận tốc 16 km/h trong y giờ. Biểu thức biểu thị tổng quãng đường hai bạn đi được và giá trị của nó với x = 1; y = 0,5 lần lượt là

A. 12x + 16y (km) và 20 km;

B. 12(x + 16y) (km) và 108 km;

C. 12y + 16x (km) và 20 km;

D. 28(x + y) (km) và 42 km.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A

Quãng đường An đi được là: 12x (km).

Quãng đường Bình đi được là: 16y (km).

Tổng quãng đường hai bạn đi được là: S = 12x + 16y (km).

Thay x = 1; y = 0,5 vào biểu thức S, ta có S = 12.1 + 16.0,5 = 20 (km).

Câu 5:

Cho hai đa thức:

$A = 3 a x^{3} + \frac{4}{5} a x^{2} y^{2} + \frac{3}{4} x y^{3} + 2$ và $a x^{3} + \frac{4}{5} b x^{2} y^{2} + 1$ , với a, b là hằng số.

Tại x = 2; y = 1, biểu thức A - B có dạng $\frac{m}{5} a - \frac{n}{5} b + \frac{5}{2}$ . Giá trị của m - n là

A. 80;

B. 112;

C. 16;

D. 77.

Xem đáp án

Câu 6:

Cho

A = x y^{2} + \sqrt{3} y z

và B = -xy² - yz + 8. Khi đó, giá trị của biểu thức M = A + B tại x = - 2; y = |x|; z = |y| là một số chia hết cho

A. 2;

B. 3;

C. 5;

D. 9.

Xem đáp án

Câu 7:

Cho đa thức M thỏa mãn 13x²y⁴ + M = 12x²y⁴ + xy² - 3. Giá trị của đa thức M tại $x = \frac{1}{2}; y = 2$ là

A. 3;

B. -5;

C.

\frac{‐ 11}{4}

;

D.

\frac{‐ 9}{4}

.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B

Ta có: 13x²y⁴ + M = 12x²y⁴ + xy² - 3

Suy ra M = 12x²y⁴ + xy² - 3 - 13x²y⁴

= (12x²y⁴ - 13x²y⁴) + xy² - 3

= -x²y⁴ + xy² - 3.

Thay $x = \frac{1}{2}; y = 2$ vào đa thức M đã thu gọn, ta được:

.

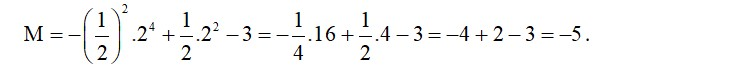
Câu 8:

Cho hai đa thức M = 4xy – 6x³ + 7x² – 12y³ + 38y² + 10x – 15y + 22 và N = 7x³ – 18y² + 24xy + 6x² – 13y² + 27. Giá trị của biểu thức P = 2M + N tại x = 1 và y = 2 là

A. 88;

B. 90;

C. 95;

D. 98.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D

Ta có P = 2M + N

= 2(4xy – 6x³ + 7x² – 12y³ + 38y² + 10x – 15y + 22) + 7x³ – 18y² + 24xy + 6x² – 13y² + 27

= 8xy – 12x³ + 14x² – 24y³ + 76y² + 20x – 30y + 44 + 7x³ – 18y² + 24xy + 6x² – 13y² + 27

= (8xy + 24xy) + (– 12x³ + 7x³) + (14x² + 6x²) – 24y³ + (76y² – 18y²– 13y²) + 20x – 30y + (44 + 27)

= 32xy – 5x³ + 20x² – 24y³ + 45y² + 20x – 30y + 71

Thay x = 1 và y = 2 vào biểu thức P, ta được:

P = 32.1.2 – 5.1³ + 20.1² – 24.2³ + 45.2² + 20.1 – 30.2 + 71

= 64 – 5 + 20 – 192 + 180 + 20 – 60 + 71

= 98.

Câu 9:

Cho đa thức A thỏa mãn tổng của A với đa thức 3xy² + 3xz² – 3xyz – 8y²x + 10 là đa thức không. Giá trị của biểu thức A tại x = –1; y = 2 và z = 0 là

A. 30;

B. –10;

C. –30;

D. 10.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A

Ta có A + 3xy² + 3xz² – 3xyz – 8y²x + 10 = 0

Suy ra A = –3xy² – 3xz² + 3xyz + 8xy² – 10

= 5xy² – 3xz² + 3xyz – 10

Thay x = –1; y = 2 và z = 0 vào biểu thức A đã thu gọn, ta được:

A = 5.(–1).2² – 3.(–1).0² + 3.(–1).2.0 – 10

= –20 – 10 = –30.

Câu 10:

Cho đa thức M thỏa mãn ${(\frac{‐ 1}{2} a x)}^{2} . {(b y^{2})}^{2} + 1 - 2 M = 2 {(b^{2} y^{2})}^{2} - 1$ , với a, b là hằng số khác 0. Giá trị của M tại $x = \frac{1}{a b}; y = 2$ là

A. -16a²b⁴ - 3;

B. $\frac{1}{8} a^{2} b^{2} - 4 b^{4} + 1$ ;

C. -16b⁴ + 3;

D. $\frac{1}{8} a^{2} b^{2} + 2 b^{4} + 1$ .

Xem đáp án