Dạng 1. Trường hợp đồng dạng thứ nhất của tam giác
-
266 lượt thi
-
10 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Cho tam giác ABC có AB = 3 cm, AC = 5 cm, BC = 7 cm. Tam giác A'B'C' có A'B' = 6 cm, B'C' = 14 cm, A'C' = 10 cm. Khi đó tam giác BAC đồng dạng với:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B
Ta có .
Suy ra .
Xét hai tam giác BAC và B'A'C' có .
Suy ra ΔBAC ᔕ ΔB'A'C' (c – c – c).
Câu 3:
Cho tam giác ABC vuông tại A và tam giác A'B'C' vuông tại A' có . Khi đó bằng:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C
Xét hai tam giác ABC và A'B'C' có:
Do đó, ΔABC ᔕ ΔA'B'C' (ch – cgv).
Suy ra .
Suy ra .
Câu 4:
Cho tam giác ABC đồng dạng với tam giác DEF. Biết AB = 6 cm, BC = 10 cm, AC = 14 cm và chu vi tam giác DEF bằng 45 cm. Độ dài các cạnh của tam giác DEF là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A
Chu vi tam giác ABC là:
6 + 10 + 14 = 30 (cm).
Vì ΔABC ᔕ ΔDEF nên .
Suy ra .
Do đó,
, , .
Câu 5:
Cho tam giác ABC có AB = 4 cm, BC = 5 cm, AC = 6 cm và tam giác MNP có MN = 2 cm, NP = 3 cm, MP = 2,5 cm. Chọn đáp án đúng.
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D
Ta có .
Suy ra .
Xét hai tam giác ABC và NPM có .
Suy ra ΔABC ᔕ ΔNMP (c – c – c).
Câu 6:
Tứ giác ABCD có AB = 3 cm, BC = 10 cm, CD = 12 cm, AD = 5 cm và BD = 6 cm. Tứ giác ABCD là hình gì?
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C
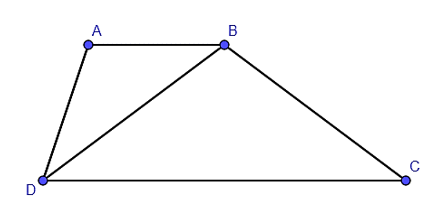
Ta có .
Suy ra .
Xét hai tam giác ABD và BDC có .
Suy ra ΔABD ᔕ ΔBDC (c – c – c).
Suy ra .
Mà hai góc này ở vị trí so le trong nên AB // DC.
Do đó, tứ giác ABCD là hình thang.
Câu 7:
Cho tam giác ABC và một điểm O nằm trong tam giác đó. Gọi M, N, P lần lượt là trung điểm của các đoạn OA, OB, OC. Khi đó tam giác MNP đồng dạng với tam giác nào?
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A
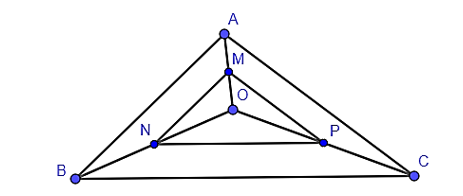
Xét tam giác OAB có:
M là trung điểm OA, N là trung điểm OB.
Suy ra MN là đường trung bình của tam giác OAB.
Suy ra hay (1).
Xét tam giác OAC có:
M là trung điểm OA, P là trung điểm OC.
Suy ra MP là đường trung bình của tam giác OAC.
Suy ra hay (2).
Xét tam giác OBC có:
N là trung điểm OB, P là trung điểm OC.
Suy ra NP là đường trung bình của tam giác OBC.
Suy ra hay (3).
Từ (1), (2), (3) suy ra .
Xét hai tam giác ABC và MNP có .
Suy ra ΔABC ᔕ ΔMNP (c – c – c).
Câu 8:
Cho tam giác ABC đồng dạng với tam giác DEF. Biết BC = 24,3 cm, CA = 32,4 cm, AB = 16,2 cm và AB – DE = 10 cm. Tính độ dài các cạnh của tam giác DEF.
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B
Vì ΔABC ᔕ ΔDEF nên .
Mà AB – DE = 10 cm nên DE = AB – 10 = 16,2 – 10 = 6,2 (cm).
Suy ra .
Suy ra .
Câu 9:
Cho hình thang vuông ABCD tại A và D, AB = 6 cm, CD = 12 cm, AD = 17 cm. Trên cạnh AD lấy E, biết AE = 8 cm, EB = 10 cm, EC = 15 cm. Khi đó bằng
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C
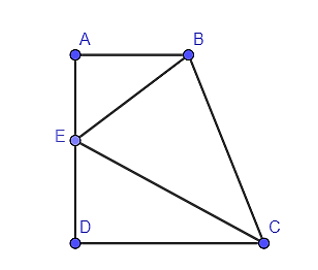
Ta có AD = AE + ED nên ED = AD – AE = 17 – 8 = 9 (cm).
Có .
Suy ra .
Xét hai tam giác ABE và DEC có:
Suy ra ΔABE ᔕ ΔDEC (ch – cgv).
Suy ra .
Mà (do tam giác DEC vuông tại D) nên .
Suy ra .
Câu 10:
Cho tam giác ABC vuông tại A có AB = 3 cm, BC = 5 cm. Cho tam giác A'B'C' đồng dạng với tam giác ABC có cạnh nhỏ nhất là 1,5 cm. Độ dài cạnh B'C' là
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C
Vì tam giác ABC vuông tại A nên theo định lí Pythagore ta có:
AB2 + AC2 = BC2.
Suy ra AC2 = BC2 – AB2 = 52 – 32 = 16.
Suy ra AC = 4 (cm).
Vì ΔABC ᔕ ΔA'B'C' nên .
Vì trong tam giác ABC cạnh AB nhỏ nhất nên trong tam giác A'B'C' cạnh A'B' nhỏ nhất
Suy ra A'B' = 1,5 cm.
Do đó, .
Suy ra (cm).

