13 câu hỏi trắc nghiệm thuộc Bài tập theo Tuần toán 8- Tuần 29_ đề 2

Bài tập theo Tuần toán 8- Tuần 29

Bài tập theo Tuần toán 8- Tuần 29_ đề 2

487 lượt thi
13 câu hỏi
45 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Cho $A B = 2 c m; C D = 4 c m$ . Khi đó $\frac{A B}{C D} = ?$

A. 5dm

B. 5

C. 1/2

D. 2/4 dm

Xem đáp án

Đáp án C

Câu 2:

Trong hình biết MQ là tia phân giác góc NMP. Tỷ số x/y là

A. 5/2

B. 5/4

C. 2/5

D. 4/5

Xem đáp án

Đáp án D

Câu 3:

Tam giác ABC đồng dạng với DEF nếu có

$A . \frac{A B}{D E} = \frac{A C}{D F}; \hat{B} = \hat{E}$

$B . \frac{A B}{D E} = \frac{A C}{D F}; \hat{A} = \hat{D}$

$C . \frac{A B}{D E} = \frac{A C}{D F}; \hat{C} = \hat{F}$

$D . \frac{A B}{D E} = \frac{B C}{D F}$

Xem đáp án

Đáp án B

Câu 4:

Nếu tam giác ABC vuông tại A và tam giác DEF vuông tại D có góc C bằng góc E thì

$A . Δ A B C ~ Δ D E F$

$B . Δ A B C ~ Δ D F E$

$C . Δ A B C ~ Δ E D F$

$D . Δ A B C ~ Δ F E D$

Xem đáp án

Đáp án B

Câu 5:

Nếu hai tam giác đồng dạng với nhau theo tỉ số đồng dạng k thì tỉ số hai đường cao của hai tam giác đó bằng:

$A . k$

$B . \frac{1}{k}$

$C . k^{2}$

$D . 2 k$

Xem đáp án

Đáp án A

Câu 6:

Cho

Δ D E F ~ Δ A B C

theo tỉ số đồng dạng

k = \frac{1}{2} .

Biết diện tích bằng

5 c m^{2}

thì diện tích

Δ A B C

sẽ là

$A . 2,5 c m^{2}$

$B . 10 c m^{2}$

$C . 20 c m^{2}$

$D . 25 c m$

Xem đáp án

Đáp án C

Câu 7:

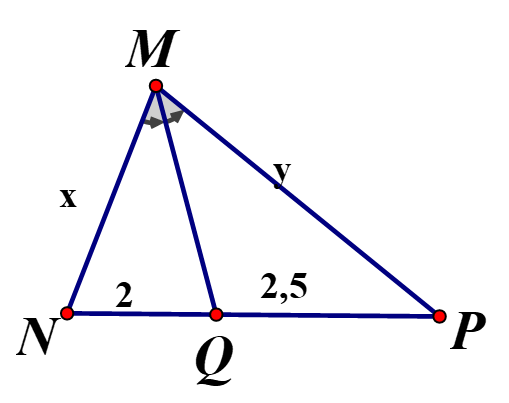
Cho tam giác MNP có MD là đường phân giác (D thuộc NP) , biết

M N = 15 c m; M P = 25 c m; N D = 7,5 c m .

Tính tỉ số $\frac{N D}{D P}$ . Từ đó tính DP và NP

Xem đáp án

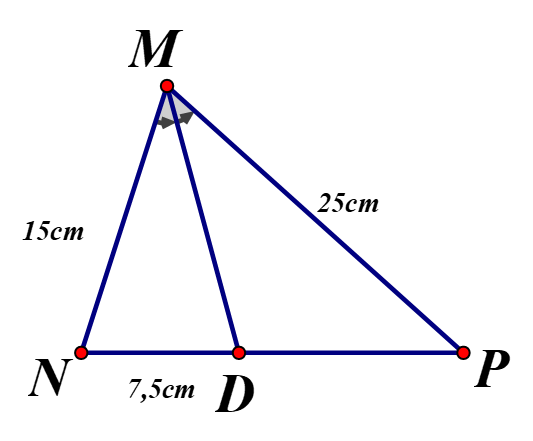
Cho tam giác MNP có MD là đường phân giác (D thuộc NP) , biết (ảnh 1)

Vì MD là đường phân giác của tam giác NMP nên $\frac{N D}{D P} = \frac{M N}{M P} \Rightarrow \frac{7,5}{D P} = \frac{15}{25} \Rightarrow D P = 12,5 c m$

$\Rightarrow N P = N D + D P = 7,5 + 12,5 = 20 (c m)$

Vậy $D P = 12,5 c m, N P = 20 c m$

Câu 8:

Cho tam giác ABC vuông tại A, có $A B = 6 c m; A C = 8 c m,$ kẻ đường cao AH cắt tia phân giác BD tại K $(H \in B C; D \in A C)$

a) Chứng minh $Δ A H B ~ Δ C A B$ . Tính AH

b) Chứng minh $Δ H B K ~ Δ A B D$ , suy ra hệ thức $B H . B D = B K . A B$

Chứng minh

Δ A K D

cân

Xem đáp án

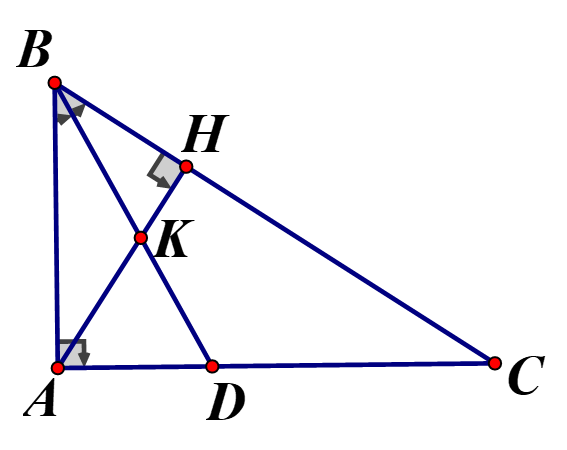
Cho tam giác ABC vuông tại A, có AB=6cm, AC=8cm kẻ đường cao AH cắt tia phân giác BD tại K (H thuộc BC, D thuộc AC) (ảnh 1)

a) Xét $Δ A H B$ và $Δ C A B$ có: $∠ B A C = ∠ A H B = 90^{0}; ∠ B$ chung

$\Rightarrow Δ A H B ~ Δ C A B (g . g)$

$\begin{array}{l} B C = \sqrt{A B^{2} + A C^{2}} = \sqrt{6^{2} + 8^{2}} = 10 (p y t a g o) \\ \Rightarrow \frac{A H}{A B} = \frac{A C}{B C} \Rightarrow A H = \frac{A B . A C}{B C} = \frac{6.8}{10} = 4,8 (c m) \end{array}$

b) Xét $Δ A B K$ và $Δ H B K$ có: $∠ B A D = ∠ B H K (= 90^{0})$

$∠ A B D = ∠ H B D$ (vì BD phân giác) $\Rightarrow Δ A B D ~ Δ H B K (g . g)$

$\Rightarrow \frac{A B}{B D} = \frac{B H}{B K} \Rightarrow B H . B D = A B . B K$

c) Ta có: $∠ A D K + ∠ A B D = 90^{0}$ (phụ nhau)

$∠ B H K + ∠ D B H = 90^{0}$ (phụ nhau)

Mà $∠ A B D = ∠ D B H (B D$ là phân giác) và $∠ B K H = ∠ A K D$ (đối đỉnh)

Nên $∠ A K D = ∠ A D K \Rightarrow Δ A D K$ cân tại A.

Câu 9:

Viết thành bất phương trình và chỉ ra một nghiệm của nó từ các mệnh đề sau

a) Tổng của một số nào đó với 7 lớn hơn 9

b) Hiệu của 12 và một số nào đó nhỏ hơn -8

Xem đáp án

$a) x + 7 > 9; b) 12 - x < - 8$

Câu 10:

Viết thành bất phương trình và chỉ ra hai nghiệm của nó từ các mệnh đề sau :

a) Tổng của 4 lần số nào đó với 5 lớn hơn 10

b) Hiệu của 18 và 4 lần số nào đó nhỏ hơn 30

Xem đáp án

$a) 4 x + 5 > 10$ có hai nghiệm $x = 4, x = 5$

$b) 18 - 4 x < 30$ có hai nghiệm $x = 1, x = 3$

Câu 11:

Với tập hợp $B = \{- 10; - 9; - 8; - 7; - 6; .......8,9,10\}$ . Hãy cho biêt số nào trong B là nghiệm của bất phương trình

$a) |x - 5| < 4 b) |x - 1| < 2$

Xem đáp án

$\begin{array}{l} a) |x - 5| < 4 \Rightarrow - 4 < x - 5 < 4 \Leftrightarrow 1 < x < 9 \\ b) |x - 1| < 2 \Rightarrow - 2 < x - 1 < 2 \Rightarrow - 1 < x < 3 \end{array}$

Câu 12:

Hãy đưa ra ba nghiệm của bất phương trình:

$a) 8 > x b) - 7 < x$

Xem đáp án

$a) 8 > x$ có 3 nghiệm $x = 1; 2; 3$

$b) - 7 < x$ có 3 nghiệm $x = - 1; - 2; - 3$

Câu 13:

Viết tập nghiệm của phương trình sau bằng ký hiệu tập hợp và biểu diễn tập nghiệm đó trên trục số :

$a) 4 < x b) - 9 > x$

Xem đáp án

$\begin{array}{l} a) 4 < x S = \{x \in ℝ / x < 4\} \\ b) - 9 > x S = \{x \in ℝ / x < - 9\} \end{array}$

Bắt đầu thi ngay