Dạng 1. Chứng minh hai tam giác đồng dạng
-
422 lượt thi
-
5 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Cho có 3 góc nhọn, các đường cao cắt nhau ở H. Chứng minh: và suy ra các kết quả tương tự.
 Xem đáp án
Xem đáp án

Vì (cùng phụ với )
Xét và có:
Tương tự ta có:
Câu 2:
Điểm H cách đều 3 cạnh của tam giác DEF
 Xem đáp án
Xem đáp án

là tia phân giác (3)
Lại có: (cùng phụ với )
Mà:
là tia phân giác (4)
Từ (3) và (4) suy ra: H là giao điểm của 3 đường phân giác trong tam giác FED hay H cách đều 3 cạnh của tam giác FED
Câu 3:
Cho hình thang ABCD (AB // CD). Gọi O là giao điểm của hai đường chéo AC và BD.
Chứng minh OA.OD = OB.OC.
 Xem đáp án
Xem đáp án
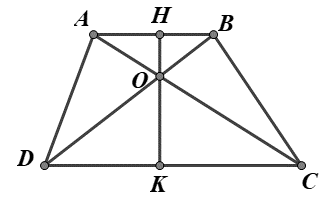
dpcm
Câu 4:
Đường thẳng qua O, vuông góc với AB, CD theo thứ tự tại H, K. Chứng minh
 Xem đáp án
Xem đáp án
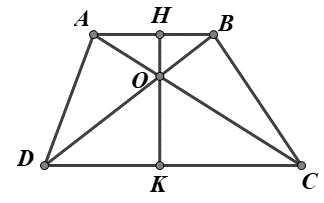
Mà nên
Câu 5:
Cho tam giác ABC có , AB = 4 cm, AC = 8 cm, Tính độ dài cạnh BC ?
 Xem đáp án
Xem đáp án
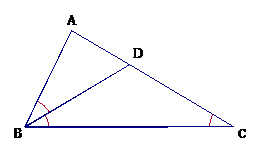
Kẻ đường phân giác BD của tam giác ABC.
Xét ∆ABC và ∆ADB có chung, suy ra ∆ABC ∆ADB (g.g)
Þ CD = 6 (cm).
∆ABC có BD là đường phân giác nên .
