8 câu hỏi trắc nghiệm thuộc Đề kiểm tra Học kì 1 Toán 8 có đáp án (Mới nhất)_ đề 5

Bộ đề kiểm tra Học kì 1 Toán 8 có đáp án (Mới nhất)

Đề kiểm tra Học kì 1 Toán 8 có đáp án (Mới nhất)_ đề 5

1126 lượt thi
8 câu hỏi
45 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Tìm x, biết: x³ + 4x + x² + 4 = 0.

A. x = 0

C. x = -2

D. x = - 1

Xem đáp án

1. D

Câu 2:

Tính chất nào dưới đây không phải của hình bình hành:

A. Tổng bốn góc bằng 360⁰.

B. Hai đường chéo bằng nhau.

C. Các cặp cạnh đối bằng nhau.

D. Hai đường chéo cắt nhau tại trung điểm mỗi đường.

Xem đáp án

2. B

Câu 3:

Hình thoi có độ dài hai đường chéo là 10cm và 24cm. Tính chu vi của hình thoi?

A. 12 cm

B. 5 cm

C. 13 cm

D. 26 cm

Xem đáp án

3. C

Câu 4:

Có bao nhiêu số tự nhiên n để đa thức

\frac{1}{3} x^{4} y^{n} - x^{3} y^{2}

chia hết cho đơn thức

- 3 x^{n} y^{2} ?

A. 0

B. 2

C. 1

D. 3

Xem đáp án

4. B

Câu 5:

Thực hiện phép tính

a) ${(x + 5)}^{2} - x (x + 10)$

(18 x^{6} y^{6} - 12 x^{5} y^{5} + 24 x^{3} y^{5}) : 6 x^{3} y^{5}

Xem đáp án

a. ${(x + 5)}^{2} - x (x + 10)$

$= x^{2} + 10 x + 25 - x^{2} - 10 x$

$= (x^{2} - x^{2}) + (10 x - 10 x) + 25$

= 25

b) $(18 x^{6} y^{6} - 12 x^{5} y^{5} + 24 x^{3} y^{5}) : 6 x^{3} y^{5}$

$= 18 x^{6} y^{6} : 6 x^{3} y^{5} - 12 x^{5} y^{5} : 6 x^{3} y^{5} + 24 x^{3} y^{5} : 6 x^{3} y^{5}$

$= 3 x^{3} y - 2 x^{2} + 4$

Câu 6:

Phân tích đa thức sau thành nhân tử

a) $a^{2} - b^{2} - 12 a + 12 b$

b) $4 x^{2} - 4 x + 1 - 25 y^{2}$

c) $x^{2} - 3 x - 10$

Xem đáp án

a) $a^{2} - b^{2} - 12 a + 12 b$

$= (a^{2} - b^{2}) + (- 12 a + 12 b)$
$= (a - b) (a + b) - 12 (a - b)$

$= (a - b) (a + b - 12)$

b) $4 x^{2} - 4 x + 1 - 25 y^{2}$

$= (4 x^{2} - 4 x + 1) - {(5 y)}^{2}$

$= {(2 x - 1)}^{2} - {(5 y)}^{2}$

= (2 x - 1 + 5 y) (2 x - 1 - 5 y)

c)

x^{2} - 3 x - 10

= x^{2} + 2 x - 5 x - 10

= x (x + 2) - 5 (x + 2)

= (x + 2) (x - 5)

Câu 7:

Cho phân thức $A = \frac{2 x - 4}{x^{2} - 4 x + 4}$ với $x \neq 2$

a) Rút gọn A

b) Tìm x nguyên để A có giá trị nguyên.

Xem đáp án

A = \frac{2 x - 4}{x^{2} - 4 x + 4} = \frac{2 (x - 2)}{{(x - 2)}^{2}} = \frac{2}{x - 2}

b) Điều kiện $x \neq 2$ , $A = \frac{2}{x - 2}$

A có giá trị nguyên $\Leftrightarrow \frac{2}{x - 2}$ có giá trị nguyên $\Leftrightarrow 2 ⋮ (x - 2)$

$\Leftrightarrow x - 2$ là ước của của 2

$\Leftrightarrow x - 2 \in$ Ư(2) = {1; -1; 2; -2}

Ta có bảng sau:

Cho phân thức A=(2x-4)/(x^2-4x+4) với x khác 2 a) Rút gọn A b) Tìm x nguyên để A có giá trị nguyên. (ảnh 1)

Vậy

x \in {1; 0; 3; 4}

thì A có giá trị nguyên

Câu 8:

Cho hình chữ nhật ABCD. Gọi M là trung điểm của BC và E là giao điểm của đường thẳng AM với đường thẳng DC.

a) Chứng minh rằng: tứ giác ABEC là hình bình hành

b) Gọi F là điểm đối xứng của B qua C. Chứng minh rằng: tứ giác BEFD là hình thoi.

c) Chứng minh rằng: C là trọng tâm tam giác AEF

d) Cho

A B^{2} = 3. B C^{2}

. Gọi H là trung điểm của DF và K là giao điểm của đường thẳng AH với đường thẳng EF. Chứng minh rằng: AE=2MK

Xem đáp án

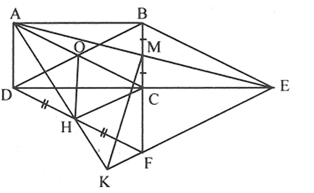
a) Xét Tam giác ABM và Tam giác ECM có:

MB=CM (M là trung điểm của BC)

$\hat{A M B} = \hat{E M C}$ (đối đỉnh),

$\hat{A B M} = \hat{E C M}$ (so le trong và AB//CD)

Do đó $Δ A B M = Δ E C M (g . c . g)$

Suy ra: AB=EC (hai cạnh tương ứng)

Mà AB//EC

Do đó tứ giác ABEC là hình bình hành (dấu hiệu nhận biết)

Ta có AB=CD, AB=CE

Suy ra: CD=CE

Tứ giác BEFD có:

C là trung điểm của DE,

C là trung điểm của BF (B và F đối xứng của C)

Do đó tứ giác BEFD là hình bình hành Mà BF vuông góc với DE

Vậy tứ giác BEFD là hình thoi

c) Ta có BC=CF, CM=BM=BC/2 (M là trung điểm của BC)

Suy ra $F C = \frac{2}{3} F M$

Tam giác AEF có FM là đường trung tuyến, C thuộc đoạn thẳng FM và

F C = \frac{2}{3} F M \Rightarrow C

là trọng tâm của tam giác AEF.

d) Tam giác ABC vuông tại B $\Rightarrow A B^{2} + B C^{2} = A C^{2}$ (định lí Py-ta-go)

Mà $A B^{2} = 3. B C^{2}$

Do đó $A C^{2} = 4 B C^{2} \Rightarrow A C = 2 A B (A C > 0)$

Gọi O là giao điểm của AC, BD

Ta cóAC=BD, O là trung điểm của AC, BD

Nên AC=BD=BF

Mặt khác O, H lần lượt là trung điểm của BD, DF

$\Rightarrow$ HO là đường trung bình của tam giác DBF $\Rightarrow H O = \frac{B F}{2}$

Tam giác HAC có HO là đường trung tuyến và $H O = \frac{A C}{2} (= \frac{B F}{2}) \Rightarrow Δ H A C$ vuông tại H $\Rightarrow A H C = 90 °$

Mà C, H lần lượt là trung điểm của DE, DF suy ra CH là đường trung bình của tam giác DEF suy ra $C H // E F \Rightarrow \hat{A K E} = \hat{A H C} = 90 °$

Ta có tam giác KAE vuông tại K, KM là đường trung tuyến

Do đó $K M = \frac{A E}{2}$

Vậy AE=2MK.

Bắt đầu thi ngay