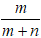Cách chứng minh phân thức là tối giản cực hay, có đáp án
-
1096 lượt thi
-
14 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Chứng minh phân thức (với n ∈ N) là tối giản:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Gọi ƯCLN của –n + 3 và n - 4 là d
⇒ (-n + 3)⋮ d và (n - 4)⋮ d
⇒ [(-n + 3) +(n - 4)] ⋮ d
⇒ -1⋮ d
⇒ d = 1 hoặc d = -1
Vậy phân thức đã cho là tối giản với ∀n ∈ N
Câu 2:
Chứng minh phân thức (với n ∈ N) là tối giản
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Gọi ƯCLN của 2n + 1 và 5n + 3 là d
⇒ (2n +1)⋮ d và (5n + 3)⋮ d
⇒ [2(5n + 3) - 5(2n + 1) ] ⋮ d
⇒ 1 ⋮ d, với ∀n ∈ N
⇒ d = 1 hoặc d = -1
Vậy phân thức đã cho tối giản với ∀n ∈ N
Câu 3:
Chứng minh phân thức là tối giản với mọi số tự nhiên n
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Gọi d là ƯCLN của 3n - 2 và 4n - 3
⇒ (3n - 2)⋮ d và (4n - 3)⋮ d
⇒ [3(4n - 3) - 4(3n - 2)] = -1⋮ d
⇒ d = 1 hoặc d = -1
Vậy phân thức đã cho tối giản với ∀n ∈ N
Câu 5:
Chứng minh phân thức (với n ∈ N) là tối giản
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Gọi ƯCLN của 2n + 1 và 5n + 3 là d
⇒ (3n + 1) ⋮ d và (5n + 2) ⋮ d
⇒ [3(5n + 2) - 5(3n + 1)] ⋮ d
⇒ 1 ⋮ d, với ∀n ∈ N
⇒ d = 1 hoặc d = -1
Vậy phân thức đã cho tối giản với ∀n ∈ N
Câu 6:
Chứng minh phân thức là tối giản với mọi số tự nhiên n
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Gọi d là ƯCLN của 12n + 1 và 30n + 2
⇒ (12n + 1)⋮ d và (30n + 2)⋮ d
⇒ [5(12n + 1) - 2(30n + 2)] ⋮ d
⇒ 1 ⋮ d, với ∀n ∈ N
⇒ d = 1 hoặc d = -1
Vậy phân thức đã cho tối giản với ∀n ∈ N
Câu 7:
Chứng minh phân thức là tối giản với mọi số tự nhiên n
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Gọi d là ƯCLN của 2n + 1 và
⇒ (2n +1)⋮ d và
⇒ 2(n + 1) ⋮ d ⇒ (2n + 2) – (2n + 1) = 1 ⋮ d
⇒ d = 1 hoặc d = -1
Vậy phân thức đã cho tối giản với ∀n ∈ N
Câu 8:
Chứng minh phân thức là tối giản với mọi số tự nhiên n
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Gọi d là ƯCLN của 2n + 5 và 3n + 7
⇒ (2n + 5)⋮ d và (3n + 7)⋮ d
⇒ [3(2n + 5) - 2(3n + 7)] = 1⋮ d
⇒ d = 1 hoặc d = -1
Vậy phân thức đã cho tối giản với ∀n ∈ N
Câu 9:
Chứng minh phân thức là tối giản với mọi số tự nhiên n
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Gọi d là ƯCLN của 5n + 7 và 7n + 10
⇒ (5n + 7)⋮ d và (7n + 10)⋮ d
⇒ [7(5n + 7) - 5(7n + 10)] = -1⋮ d
⇒ d = 1 hoặc d = -1
Vậy phân thức đã cho tối giản với ∀n ∈ N
Câu 10:
Chứng minh phân thức là tối giản với mọi số tự nhiên n
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Gọi d là ƯCLN của 3n và 3n + 1
⇒ 3n ⋮ d và (3n + 1)⋮ d
⇒ [(3n + 1) - 3n ] = 1⋮ d
⇒ d = 1 hoặc d = -1
Vậy phân thức đã cho tối giản với ∀n ∈ N
Câu 11:
Chứng minh phân thức là tối giản với mọi số tự nhiên n
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Gọi d là ƯCLN của 3n - 2 và 4n - 3
⇒ (3n - 2)⋮ d và (4n - 3)⋮ d
⇒ [3(4n - 3) - 4(3n - 2)] = -1⋮ d
⇒ d = 1 hoặc d = -1
Vậy phân thức đã cho tối giản với ∀n ∈ N
Câu 13:
Chứng minh phân thức là tối giản với mọi số tự nhiên n
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Gọi d là ƯCLN của 7n - 5 và 3n - 2
⇒ (7n - 5)⋮ d và (3n - 2)⋮ d
⇒ [3(7n - 5) - 7(3n - 2)] = -1⋮ d
⇒ d = 1 hoặc d = -1
Vậy phân thức đã cho tối giản với ∀n ∈ N
Câu 14:
Cho phân thức là phân thức tối giản. Chứng minh phân thức là phân thức tối giản
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Giả sử m, n là các số nguyên và ƯCLN(m, n) = 1 (vì 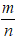
nếu d là ước chung m của m + n thì:
(m + n) d và m d
⇒ [(m + n) – m ] = n d
⇒ d ∈ ƯC (m,n) ⇒ d = 1(vì 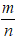
Vậy nếu phân thức