18 câu hỏi trắc nghiệm thuộc Đề kiểm tra Cuối kì 1 Toán 8 CD có đáp án (Đề 1)

Câu 1:

Cho các đơn thức $A = (0,3 + π) x^{2} y;$ $B = \frac{1}{2} x y x^{2} z;$ $C = - x y x z^{2}$ và $D = (\sqrt{2} + 1) x y^{2} z .$ Hai đơn thức thu gọn trong các đơn thức đã cho là:

A. A và B

B. A và C

C. A và D

D. B và C

Xem đáp án

Chọn đáp án C

Câu 2:

Biểu thức cần điền vào chỗ trống để có hằng đẳng thức $x^{3} + 1 = (x + 1) (x^{2} - ... + 1)$ đúng là

A. x

B. -x

C. 2x

D. -2x

Xem đáp án

Chọn đáp án A

Câu 3:

Cho phân thức $\frac{A}{B}$ với $B \neq 0.$ Nhận định nào sau đây là đúng?

A. $\frac{A}{B} = \frac{A}{- B} .$

B. $\frac{A}{B} = \frac{- B}{- A} .$

C. $\frac{A}{B} = \frac{A : N}{B : N},$ với $N \neq 0.$

D. $\frac{A}{B} = \frac{A + M}{B + M},$ với $M \neq 0.$

Xem đáp án

Chọn đáp án C

Câu 4:

Phân thức đối của phân thức $\frac{3 x}{x + y}$ là

A. $\frac{3 x}{x - y} .$

B. $\frac{x + y}{3 x} .$

C. $- \frac{3 x}{x + y} .$

D. $- \frac{3 x}{x - y} .$

Xem đáp án

Chọn đáp án C

Câu 5:

Cho hàm số $y = f (x) = 2 x^{2} - 1.$ Khẳng định nào sau đây là đúng?

A. $f (- 1) = - 3.$

B. $f (1) = 1.$

C. $f (- 1) = - 1.$

D. $f (1) = 3.$

Xem đáp án

Chọn đáp án B

Câu 6:

Cho điểm A và B trong mặt phẳng tọa độ Oxy như hình bên. Khẳng định nào sau đây là đúng?

A. N(-3;2)

B. N(2;-3)

C. M(1;-2)

D. M(-1;2)

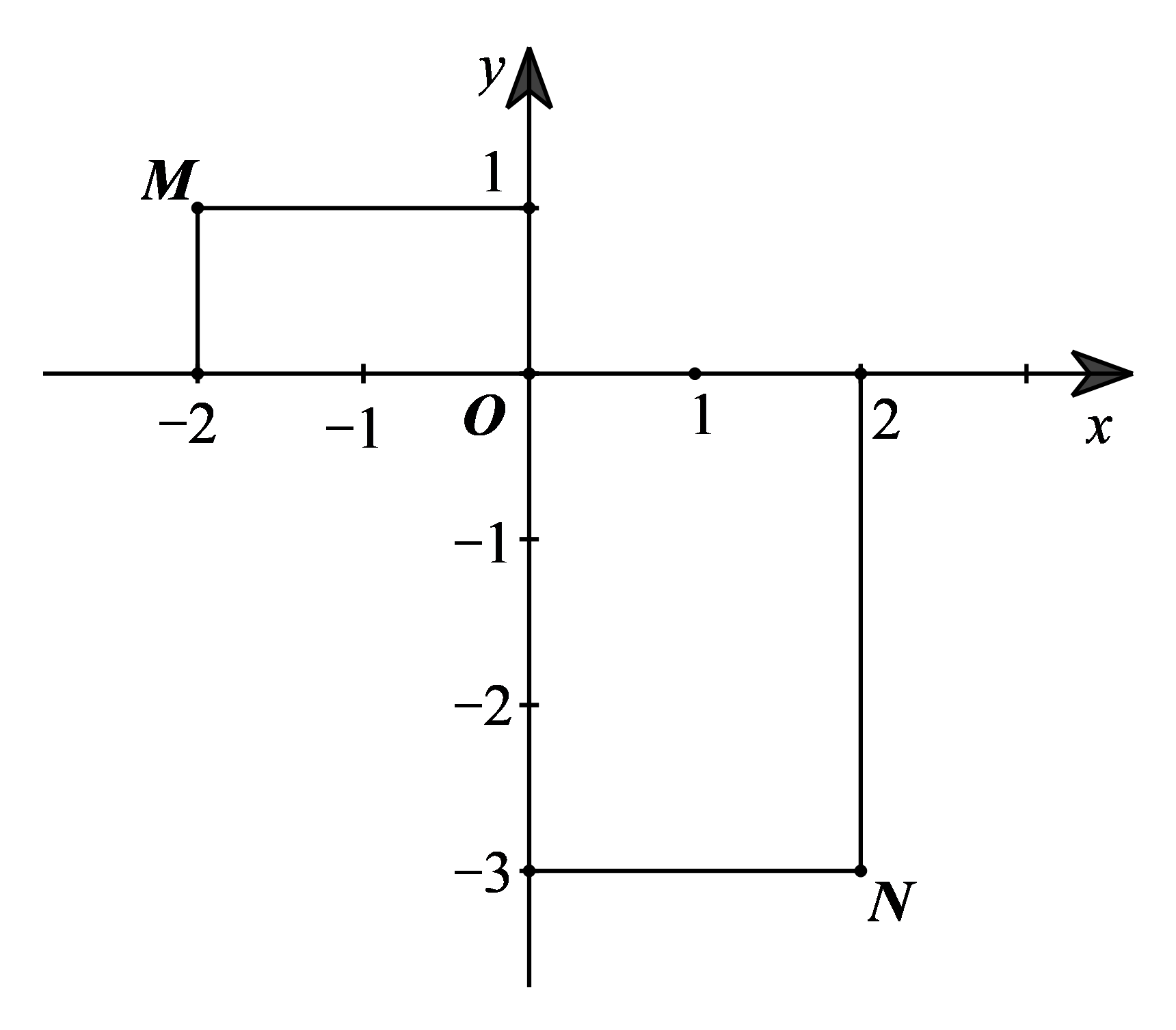
Xem đáp án

Chọn đáp án B

Câu 7:

Cho hai đường thẳng $d : y = a x + b (a \neq 0)$ và $d^{'} : y = a^{'} x + b^{'} (a^{'} \neq 0) .$ Với điều kiện nào sau đây thì hai đường thẳng d và d’ song song?

A. $a = a^{'} .$

B. $a = a^{'} .$ và $b = b^{'} .$

C. $a \neq a^{'} .$

D. $a = a^{'}$ và $b \neq b^{'} .$

Xem đáp án

Chọn đáp án D

Câu 8:

Góc tạo bởi đường thẳng $y = - 2 x + 1$ với trục Ox là

A. góc nhọn.

B. góc vuông.

C. góc tù.

D. góc bẹt.

Xem đáp án

Chọn đáp án C

Câu 9:

Tổng số cạnh bên và cạnh đáy của một hình chóp tứ giác đều là

A. 4.

B. 6.

C. 8.

D. 10.

Xem đáp án

Chọn đáp án C

Câu 10:

Một hình chóp tam giác đều có cạnh đáy là a và độ dài trung đoạn là b thì có diện tích xung quanh là

A. $S_{x q} = \frac{1}{2} a b .$

B. $S_{x q} = a b .$

C. $S_{x q} = \frac{3}{2} a b .$

D. $S_{x q} = 3 a b .$

Xem đáp án

Chọn đáp án C

Câu 11:

Một hình thang vuông có một góc bằng $75 °,$ góc còn lại không vuông của hình thang đó có số đo là

A. $25 ° .$

B. $75 ° .$

C. $105 ° .$

D. $125 ° .$

Xem đáp án

Chọn đáp án C

Câu 12:

Hình thoi cần thêm yếu tố nào để trở thành hình vuông?

A. Hai đường chéo vuông góc.

C. Hai cạnh kề bằng nhau.

D. Một đường chéo là tia phân giác của một góc.

Xem đáp án

Chọn đáp án B

Câu 13:

Phân tích các đa thức sau thành nhân tử:

a) $12 x^{4} y^{3} + 12 x^{3} y^{3} + 3 x^{2} y^{3} .$ b) $x^{4} + x y^{3} - x^{3} y - y^{4} .$

Xem đáp án

a) $12 x^{4} y^{3} + 12 x^{3} y^{3} + 3 x^{2} y^{3}$

$= 3 x^{2} y^{3} (4 x^{2} + 4 x + 1)$

$= 3 x^{2} y^{3} [{(2 x)}^{2} + 2 \cdot 2 x + 1^{2}]$

$= 3 x^{2} y^{3} {(2 x + 1)}^{2} .$

b) $x^{4} + x y^{3} - x^{3} y - y^{4}$

$= (x^{4} + x y^{3}) - (x^{3} y + y^{4})$

$= x (x^{3} + y^{3}) - y (x^{3} + y^{3})$

$= (x - y) (x^{3} + y^{3})$

$= (x - y) (x + y) (x^{2} - x y + y^{2}) .$

Câu 14:

Cho biểu thức $N = (\frac{1}{x + 1} + \frac{1}{x - 1} + \frac{x^{2}}{x^{2} - 1}) \cdot \frac{x - 1}{2 + x} .$

a) Viết điều kiện xác định của biểu thức N

b) Rút gọn biểu thức N

c) Tính giá trị của biểu thức N khi |x| = 2

Xem đáp án

a) Ta có $x^{2} - 1 = (x - 1) (x + 1) .$

Điều kiện xác định của biểu thức N là $x + 1 \neq 0,$ $x - 1 \neq 0,$ $2 + x \neq 0$ và $x^{2} - 1 \neq 0$

Hay $x \neq - 1,$ $x \neq 1$ và $x \neq - 2.$

Vậy biểu thức N xác định khi $x \neq - 1,$ $x \neq 1$ và $x \neq - 2.$

b) Với $x \neq - 1,$ $x \neq 1$ và $x \neq - 2.$ ta có:

$N = (\frac{1}{x + 1} + \frac{1}{x - 1} + \frac{x^{2}}{x^{2} - 1}) \cdot \frac{x - 1}{2 + x}$

$= \frac{1}{x + 1} \cdot \frac{x - 1}{2 + x} + \frac{1}{x - 1} \cdot \frac{x - 1}{2 + x} + \frac{x^{2}}{(x - 1) (x + 1)} \cdot \frac{x - 1}{2 + x}$

$= \frac{x - 1}{(x + 1) (2 + x)} + \frac{1}{2 + x} + \frac{x^{2}}{(x + 1) (2 + x)}$

$= \frac{x - 1 + x + 1 + x^{2}}{(x + 1) (2 + x)}$

$= \frac{x^{2} + 2 x}{(x + 1) (x + 2)}$

$= \frac{x (x + 2)}{(x + 1) (x + 2)} = \frac{x}{x + 1} .$

Vậy với $x \neq - 1,$ $x \neq 1$ và $x \neq - 2,$ thì $N = \frac{x}{x + 1} .$

c) Ta có $|x| = 2$ suy ra $x = 2$ (thỏa mãn điều kiện) hoặc $x = - 2$ (không thỏa mãn điều kiện).

Thay $x = 2$ vào biểu thức $N = \frac{x}{x + 1},$ ta được:

$N = \frac{2}{2 + 1} = \frac{2}{3} .$

Vậy $N = \frac{2}{3}$ khi $|x| = 2.$

Câu 15:

Hàm chi phí đơn giản nhất là hàm chi phí bậc nhất y = ax + b trong đó b biểu thị chi phí cố định của hoạt động kinh doanh và hệ số a biểu thị chi phí của mỗi mặt hàng được sản xuất. Giả sử rằng một xưởng sản xuất xe đạp có chi phí cố định hằng ngày là 36 triệu đồng và mỗi chiếc xe đạp có chi phí sản xuất là 1,8 triệu đồng.

a) Viết công thức của hàm số bậc nhất biểu thị chi phí y (triệu đồng) để sản xuất x (xe đạp) trong một ngày.

b) Có thể sản xuất bao nhiêu chiếc xe đạp trong ngày, nếu chi phí trong ngày đó là 72 triệu đồng?

Xem đáp án

a) Công thức của hàm số bậc nhất biểu thị chi phí y (triệu đồng) để sản xuất x (xe đạp) trong một ngày là:

$y = 1,8 x + 36$ (triệu đồng).

b) Do chi phí trong ngày đó là 72 triệu đồng nên y = 72 (triệu đồng).

Thay y = 72 vào công thức $y = 1,8 x + 36$ ta có:

$1,8 x + 36 = 72$

$1,8 x = 36$

$x = 20$

Vậy với chi phí là 72 triệu đồng thì trong ngày đó có thể sản xuất được 20 chiếc xe đạp.

Câu 16:

Bạn Hà làm một cái lồng đèn hình quả trám (xem hình bên) là hình ghép từ hai hình chóp tứ giác đều có cạnh đáy 20 cm, cạnh bên 26 cm, khoảng cách giữa hai đỉnh của hai hình chóp là 30 cm.

a) Tính thể tích của lòng đèn.

b) Bạn Hà muốn dán giấy mờ lên cái lòng đèn hình quả trám này thì cần phải chuẩn bị bao nhiêu mét vuông giấy (bỏ qua các mép dán)?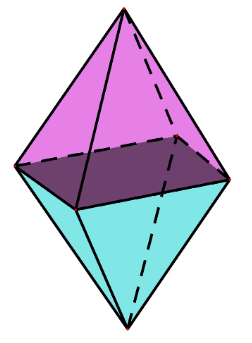

Bạn Hà làm một cái lồng đèn hình quả trám (xem hình bên) là hình ghép từ hai hình chóp tứ giác đều có cạnh đáy 20 cm, cạnh bên 26 cm (ảnh 1)

Xem đáp án

a) Chiều cao của mỗi hình chóp tứ giác đều là $30 : 2 = 15 (cm) .$

Thể tích của lồng đèn quả trám là: $V = 2 \cdot (\frac{1}{3} \cdot 20^{2} \cdot 15) = 4 000 ({cm}^{3}) .$

b) Một nửa lồng đèn được mô tả bởi hình chóp S.ABCD với các kích thước như hình vẽ.

Gọi M là trung điểm của BC Do đó $M B = M C = \frac{1}{2} B C = \frac{1}{2} \cdot 20 = 10 (cm) .$

Vì $Δ S B C$ cân tại S nên đường trung tuyến SM đồng thời là đường cao, do đó $S M ⊥ B C$ nên $Δ S B M$ vuông tại M

Áp dụng định lí Pythagore cho $Δ S B M$ vuông tại M ta có:

$S B^{2} = S M^{2} + M B^{2}$

Suy ra $S M^{2} = S B^{2} - M B^{2} = 26^{2} - 10^{2} = 676 - 100 = 576.$

Do đó $S M = 24 (cm) .$

Diện tích xung quanh (diện tích 4 mặt bên) của hình chóp tứ giác đều là:

$S_{x q} = \frac{1}{2} \cdot (4 \cdot 20) \cdot 24 = 960 ({cm}^{2}) .$

Vậy diện tích giấy mờ bạn Hà cần chuẩn bị để làm lồng đèn hình quả trám đó là:

$S = 2 S_{x q} = 2 \cdot 960 = 1 920 ({cm}^{2}) .$

Câu 17:

Cho tam giác ABC nhọn có AB < AC. Gọi N là trung điểm của AC. Lấy điểm D trên tia BN sao cho BN = ND. Kẻ $A P ⊥ B C, C Q ⊥ A D .$

a) Chứng minh N là trung điểm của PQ.

b) Tam giác ABC cần thêm điều kiện gì để tứ giác ABCD là hình vuông.

Xem đáp án

Cho tam giác ABC nhọn có AB < AC. Gọi N là trung điểm của AC. Lấy điểm D trên tia BN sao cho BN = ND. (ảnh 1)

a) Tứ giác ABCD có hai đường chéo AC, BD cắt nhau tại trung điểm N của mỗi đường nên ABCD là hình bình hành.

Do đó $A D // B C .$

Ta có $A P ⊥ B C; A D // B C$ suy ra $A P ⊥ A D$ hay $\hat{P A Q} = 90 °$ .

Vì $A P ⊥ B C, C Q ⊥ A D$ nên $\hat{A P C} = 90 °; \hat{A Q C} = 90 °$ .

Tứ giác APCQ có $\hat{P A Q} = 90 °$ ; $\hat{A P C} = 90 °; \hat{A Q C} = 90 °$ nên là hình chữ nhật.

Khi đó hai đường chéo AC, PQ cắt nhau tại trung điểm của mỗi đường.

Mà N là trung điểm của AC nên N là trung điểm của PQ.

b) Theo câu a, ABCD là hình bình hành, nên để ABCD là hình vuông thì ta cần thêm điều kiện $A B ⊥ B C, A B = B C$ hay $Δ A B C$ vuông cân tại B

Vậy để tứ giác ABCD là hình vuông thì tam giác ABC vuông cân tại B.

Câu 18:

Cho hai số x, y khác 0 thỏa mãn $x^{2} + \frac{8}{x^{2}} + \frac{y^{2}}{8} = 8$ . Tìm giá trị nhỏ nhất của biểu thức $A = x y + 2024.$

Xem đáp án

Theo đề bài: $x^{2} + \frac{8}{x^{2}} + \frac{y^{2}}{8} = 8$ suy ra $2 x^{2} + \frac{16}{x^{2}} + \frac{y^{2}}{4} = 16$

Ta có: $2 x^{2} + \frac{16}{x^{2}} + \frac{y^{2}}{4} = (x^{2} + \frac{16}{x^{2}} - 8) + (x^{2} + \frac{y^{2}}{4} + x y) - x y + 8$

= {(x - \frac{4}{x})}^{2} + {(x + \frac{y}{2})}^{2} - x y + 8.

Mà $2 x^{2} + \frac{16}{x^{2}} + \frac{y^{2}}{4} = 16$ nên ${(x - \frac{4}{x})}^{2} + {(x + \frac{y}{2})}^{2} - x y + 8 = 16$

Do đó ${(x - \frac{4}{x})}^{2} + {(x + \frac{y}{2})}^{2} = x y + 8.$

Nhận xét: Với mọi x, y ta có ${(x - \frac{4}{x})}^{2} \geq 0, {(x + \frac{y}{2})}^{2} \geq 0$

Do đó $x y + 8 \geq 0$ hay $x y \geq - 8.$

Khi đó $A = x y + 2 024 \geq - 8 + 2 024 = 2 016.$

Dấu “=” xảy ra khi và chỉ khi $\{\begin{cases} {(x - \frac{4}{x})}^{2} = 0 \\ {(x + \frac{y}{2})}^{2} = 0 \end{cases}$ hay $\{\begin{cases} x - \frac{4}{x} = 0 \\ x + \frac{y}{2} = 0 \end{cases}$ tức là $\{\begin{cases} x^{2} - 4 = 0 \\ y = - 2 x \end{cases}$ nên $\{\begin{cases} x = 2 \\ y = - 4 \end{cases}$ hoặc $\{\begin{cases} x = - 2 \\ y = 4 \end{cases} .$

Vậy giá trị nhỏ nhất của biểu thức A là 2016 khi $(x; y) \in \{(2; - 4); (- 2; 4)\} .$